Research Article, Res Rep Math Vol: 2 Issue: 2
Generalized Hybrid Block Method for Solving Second Order Ordinary Differential Equations Directly
Kuboye JO1*, Omar Z2, Abolarin OE1 and Abdelrahim R3
1Department of Mathematics, Faculty of Sciences, Federal University Oye- Ekiti, Ekiti-State, Nigeria
2Department of Mathematics, School of Quantitative Sciences, Universiti Utara Malaysia (UUM), Malaysia
3Al Jouf University, Saudi Arabia
*Corresponding Author : Kuboye JO
Department of Mathematics, Faculty of Sciences, Federal University Oye-Ekiti, Ekiti-State, Nigeria
Tel: (234) 8165396888
E-mail: kubbysholly2007@gmail.com
Received: August 18, 2017 Accepted: March 09, 2017 Published: February 23, 2018
Citation: Kuboye JO, Omar Z, Abolarin OE, Abdelrahim R (2018) Generalized Hybrid Block Method for Solving Second Order Ordinary Differential Equations Directly. Res Rep Math 2:2
Abstract
In this article, three steps block method with three generalised hybrid points is developed for the solution of second order initial value problems of ordinary differential equations. The derivation of this method is achieved through interpolation and collocation technique where power series approximate solution is employed as the basis function. In comparing the new method with existing methods, specific hybrid points are selected for solving some second order initial value problems. The results generated outperform the existing methods in terms of error.
Keywords: Power series; Interpolation; Collocation; Hybrid points; Block method; Second order ordinary differential equations
Introduction
In this paper, the numerical technique for solving directly second order initial value problems of ordinary differential equations (ODEs) of the form
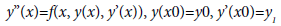 (1)
(1)
is examined. The reduction of (1) to a system of first order ODEs is associated with the following setbacks which include lot of shuman efforts and many functions to be evaluated per iteration which may jeopardize the accuracy of the method as discussed in Lambert, Fatunla, Brugnano and Trigiante, Awoyemi and Jator [1-5]. The introduction of specific hybrid points between grid points has been considered in the development of numerical methods for solving ODEs directly by some scholars namely Kayode and Adeyeye, Odejide and Adeniran, Sagir, Yap, Ismail and Senu amongst others [6-9].
In order to bring improvement on numerical methods, this article discusses the derivation of a three–step block method with three generalised hybrid points for the solution of (1) directly.
Also in examining the accuracy of the new method and for the purpose of comparison with some existing methods, a specific hybrid point is selected.
Derivation of the Method
In developing this method, power series of the form
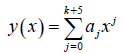 (2)
(2)
Is considered as an approximate solution to Eq. (1), where k=3. Eq. (3) is derived by differentiating Eq. (2) twice to give
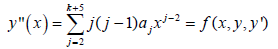 (3)
(3)
Interpolating Eq.(2) at x=x=n+i, i=0,1 and collocating (3) at x=x=n+m, m=0,v,1, (v+1),2, (v+2), 3. where 0<v<1. These equations are then combined to give a nonlinear system of equations of the form
AX=B (4)
Where
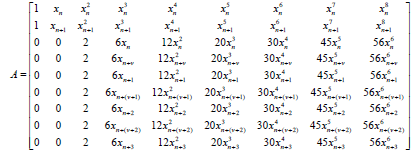
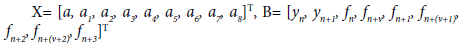
Gaussian elimination technique is used in finding the values of aj’s in (4) which are then substituted into (2) to produce a continuous implicit scheme of the form
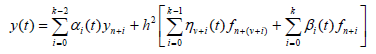 (5)
(5)
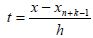
α0(t)=(-t-1)
α1(t)=(t+2)
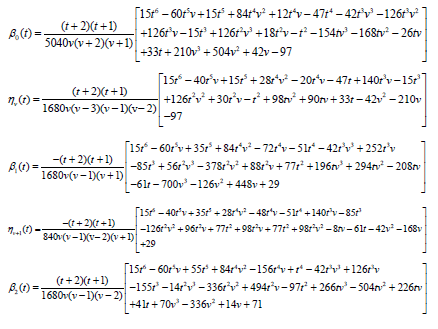
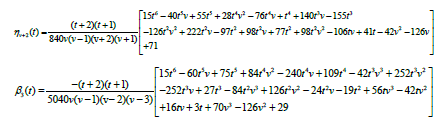
In deriving the discrete schemes, Eq. (5) is evaluated at the non-interpolating points, i.e. at x=xn+m, m=v, (v+1),2, (v+2),3 while the derivative of the scheme is derived by evaluating the derivative of (5) at all the grid points, i.e. at x=xn+m, m=0,v,1 (v+1),2, (v+2),3. This discrete scheme and its derivative at point xn are combined in a matrix form
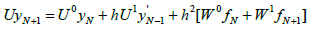 (6)
(6)
Where
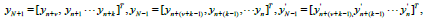
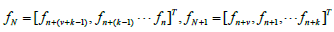 and U, U0, U1, W, W1 are nxn matrices. Therefore, the inverse of U is multiplied by (6) and this yield the block method (7)
and U, U0, U1, W, W1 are nxn matrices. Therefore, the inverse of U is multiplied by (6) and this yield the block method (7)
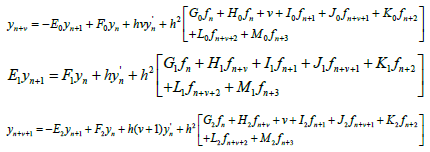
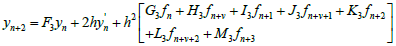 (7)
(7)
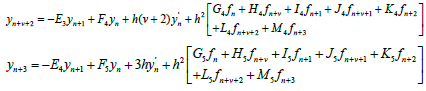
Where
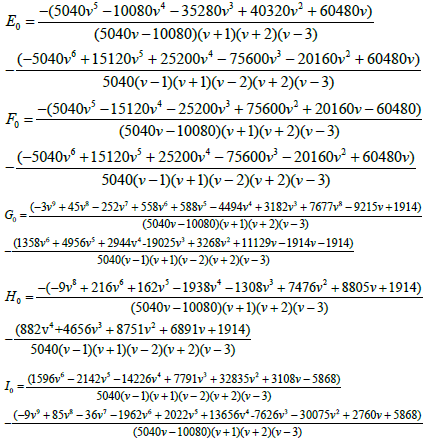
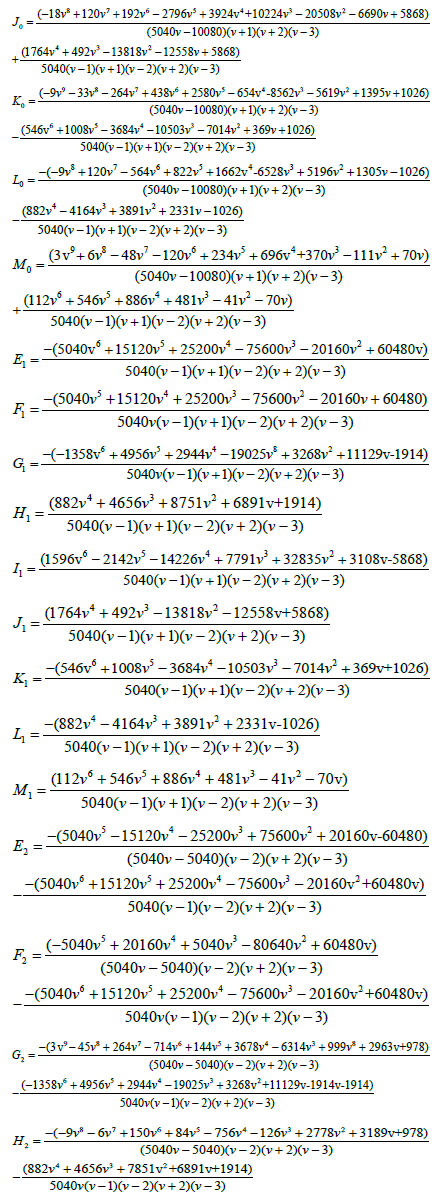
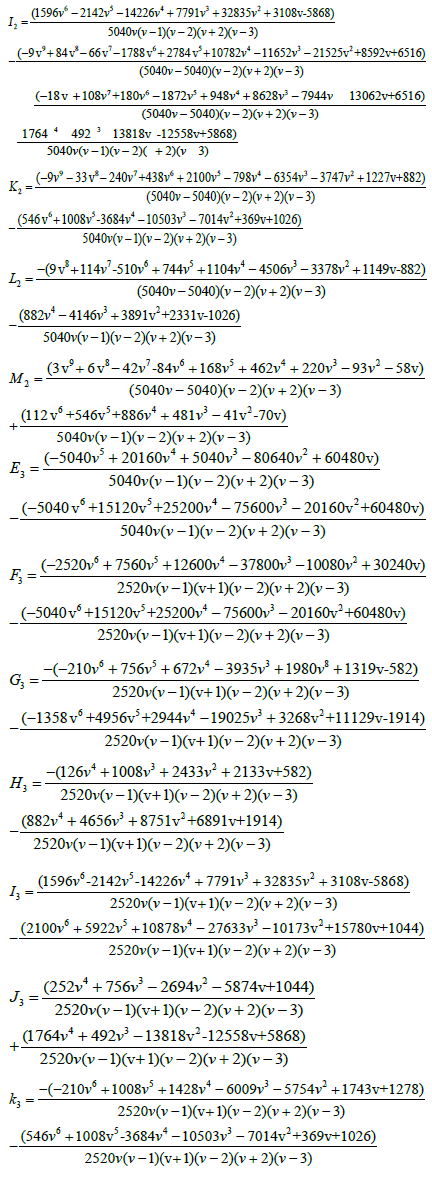
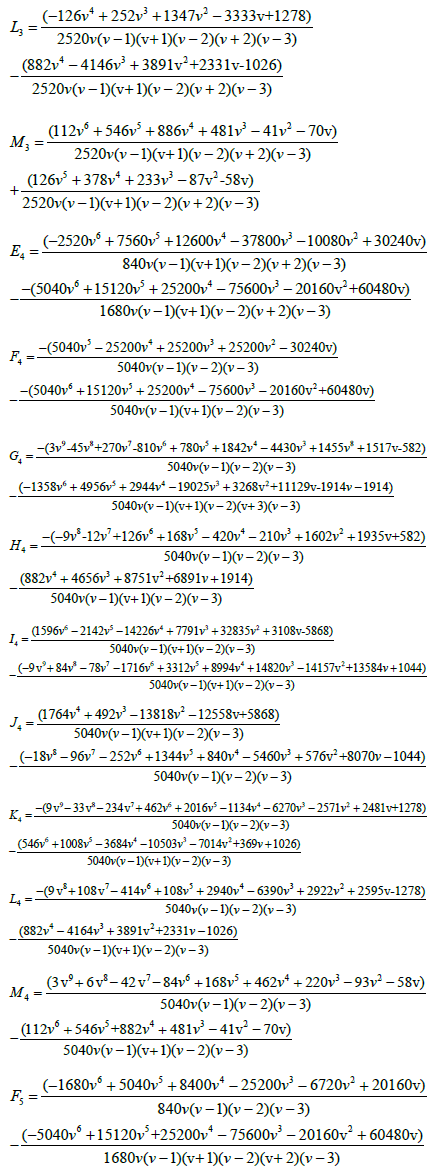
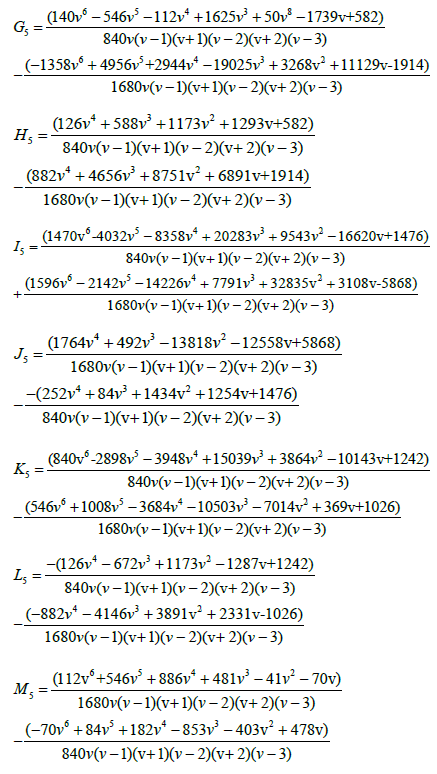
The derivative of the generalized hybrid block (7) gives
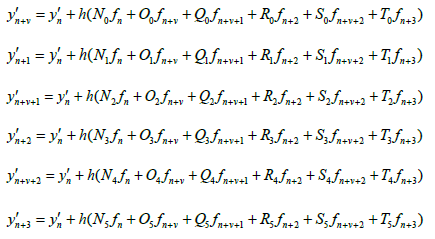
Where
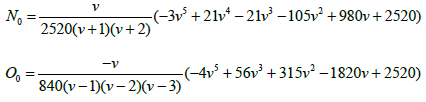
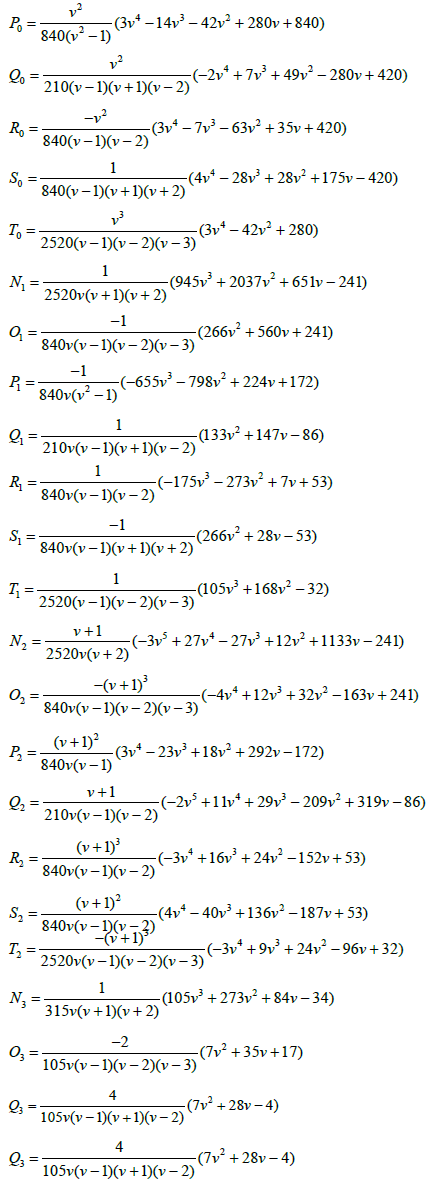
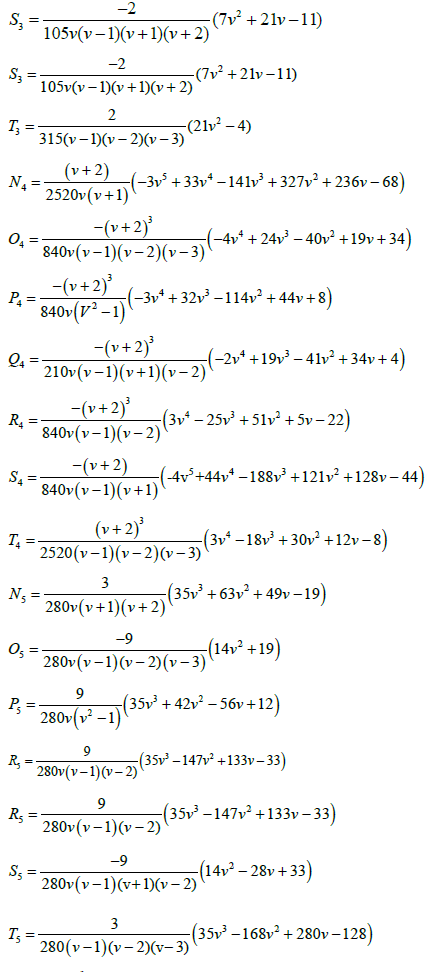
When 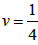 This produces the block with its derivative
This produces the block with its derivative
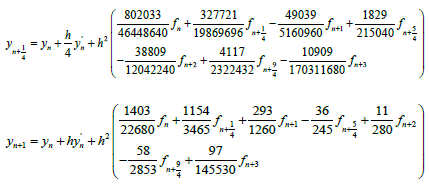
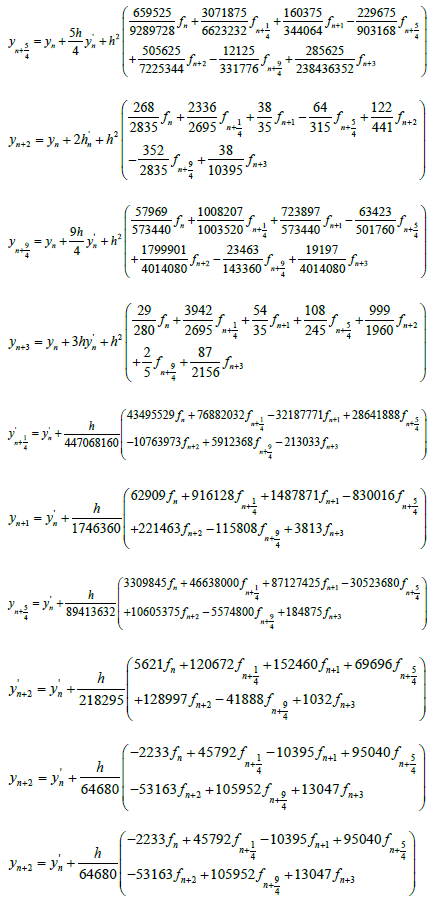
Test Problems
The following second order initial value problems of ODEs are considered in order to examine the accuracy of the new developed method.
Problem 1: y”-100y=0, y(0)=1, y’(0)=-10, h=0.01
Exact Solution: y(x)=e-10x
Problem 2: 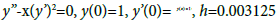
Exact Solution: 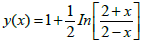
Problem 3: y”= y’, y(0)=0, y’(0)=-1, h=0.01
Exact Solution: y(x)=1-ex
Discussion of Result
It is apparent in Tables 1 and 2 that the results of the new hybrid block method k=3 outperform Awari et al. [10] k=6, Awari and Abada [11] k=7, Kuboye (2015) k=6 and Adeniyi and Alabi [12] k=6 for solving Problems 1 and 2 despite the high step-lengths k involved in these methods. Furthermore, in Table 3, the results of the new block method k=3 are better when compared with Kuboye et al. [13] k=5, Mohammed and Adeniyi [14] k=5 and Mohammed [15] k=5 for solving Problem 2.
| x-values | Exact Solution | Computed Solution | Error in New method, k=3 | Error in Awari et al. (2014) k=6 , h=0.01 | Error in Awari & Abada (2014) k=7, h=0.01 |
|---|---|---|---|---|---|
| 0.1 | 0.367879441171442330 | 0.367879441282827010 | 1.113847E-10 | 1.353E-07 | 1.440E-08 |
| 0.2 | 0.135335283236612730 | 0.135335283744420470 | 5.078077E-10 | 3.658E-07 | 3.850E-08 |
| 0.3 | 0.049787068367863944 | 0.049787069884009189 | 1.516145E-09 | 6.051E-07 | 6.330E-08 |
| 0.4 | 0.018315638888734165 | 0.018315643082197818 | 4.193464E-09 | 8.502E-07 | 8.800E-08 |
| 0.5 | 0.006737946999085461 | 0.006737958432813206 | 1.143373E-08 | 1.104E-06 | 1.151E-07 |
| 0.6 | 0.002478752176666354 | 0.002478783272535241 | 3.109587E-08 | 1.369E-06 | 1.427E-07 |
| 0.7 | 0.000911881965554514 | 0.000911966499798363 | 8.453424E-08 | 1.450E-06 | 1.716E-07 |
| 0.8 | 0.000335462627902511 | 0.000335692418749578 | 2.297908E-07 | 1.597E-06 | 1.796E-07 |
| 0.9 | 0.000123409804086679 | 0.000124034441604693 | 6.246375E-07 | 1.763E-06 | 1.941E-07 |
| 0.1 | 0.000045399929762485 | 0.000047097871085910 | 1.697941E-06 | 1.946E-06 | 2.109E-07 |
Table 1: Comparison of the New Hybrid Block Method with Uniform Accurate Block Integrators (Awari et al., 2014) and Zero Stable Continuous Block Method (Awari & Abada, 2014) for Solving Problem 1.
| x-values | Exact Solution | Computed Solution | Error in new Method, k=3, | Error in Kuboye (2015) Method, k=6, h=0.1 | Error in Adeniyi and Alabi (2011) k=6, h=0.1 | Error in Adeniyi and Alabi (2011) k=6, h=0.1 |
|---|---|---|---|---|---|---|
| 0.1 | 1.050041729278491400 | 1.050041729279076500 | 5.850875E-13 | 9.577668E-10 | 0.1329867326E-09 | 0.1708719055E-09 |
| 0.2 | 1.100335347731075600 | 1.100335347733924400 | 2.848832E-12 | 2.368709E-09 | 0.5872691257E-08 | 0.6836010114E-08 |
| 0.3 | 1.151140435936466800 | 1.151140435930138000 | 6.328715E-12 | 3.732243E-09 | 0.1327845616E-07 | 0.1555757709E-07 |
| 0.4 | 1.202732554054082100 | 1.202732547297689700 | 6.756392E-09 | 5.475119E-09 | 0.2317829012E-07 | 0.2880198295E-07 |
| 0.5 | 1.255412811882995200 | 1.255412798081808400 | 1.380119E-08 | 1.142189E-08 | 0.3218793564E-07 | 0.4802328029E-07 |
| 0.6 | 1.309519604203111900 | 1.309519582454941500 | 2.174817E-08 | 4.567944E-08 | 0.6871246012E-07 | 0.7628531256E-07 |
| 0.7 | 1.365443754271396400 | 1.365443646966158600 | 1.073052E-07 | 2.055838E-06 | 0.1012728156E-06 | 0.1157914170E-06 |
| 0.8 | 1.423648930193601700 | 1.423648730059607500 | 2.001340E-07 | 4.248299E-06 | 0.1231093271E-06 | 0.1727046080E-06 |
| 0.9 | 1.484700278594052000 | 1.484699969755750100 | 3.088383E-07 | 6.660458E-06 | 0.2019286712E-06 | 0.2561456831E-06 |
| 1.0 | 1.549306144334054800 | 1.549305163826689900 | 9.805074E-07 | 9.445166E-06 | 0.2990871645E-06 | 0.3815695118E-06 |
Table 2: Comparison of the New Hybrid Block Method with Block Method (Kuboye, 2015), Numerical Methods (Adeniyi & Alabi, 2011) where two Continuous Collocation Methods for k=6 were considered for Solving Problem 2.
| x-values | Exact Solution | Computed Solution | Error in new Method, k=3 h=0.1 | Error in Kuboye (2015) Method, k=5 h=0.1 | Error in Mohammed and Adeniyi (2014), k=5, h=0.1 | Error in Mohammed (2011), k=5, h=0.1 |
|---|---|---|---|---|---|---|
| 0.1 | -0.105170918075647710 | -0.105170918075644850 | 2.858824E-15 | 2.508826E-13 | 2.004000000E-07 | 2.198000000E-05 |
| 0.2 | -0.221402758160169850 | -0.221402758158730170 | 1.439682E-12 | 6.493175E-11 | 5.386000000E-07 | 6.070400000E-06 |
| 0.3 | -0.349858807576003180 | -0.349858807520089350 | 5.591383E-11 | 1.683146E-09 | 8.840000000E-07 | 1.005100000E-05 |
| 0.4 | -0.491824697641270350 | -0.491824692844668230 | 4.796602E-09 | 1.700635E-08 | 1.229700000E-06 | 1.402530000E-05 |
| 0.5 | -0.648721270700128190 | -0.648721260662319610 | 1.003781E-08 | 1.025454E-07 | 1.575200000E-06 | 1.799340000E-05 |
| 0.6 | -0.822118800390508890 | -0.822118784488882760 | 1.590163E-08 | 2.558711E-06 | 1.920400000E-06 | 2.161620000E-05 |
| 0.7 | -1.013752707470476600 | -1.013752678770335700 | 2.870014E-08 | 5.273300E-06 | 2.506000000E-06 | 2.799300000E-05 |
| 0.8 | -1.225540928492467900 | -1.225540885645167900 | 4.284730E-08 | 8.275935E-06 | 3.106000000E-06 | 3.456100000E-05 |
| 0.9 | -1.459603111156949900 | -1.459603052578256800 | 5.857869E-08 | 1.161667E-05 | 3.705000000E-06 | 4.111400000E-05 |
| 0.1 | -1.718281828459045500 | -1.718281743966074900 | 8.449297E-08 | 1.542187E-05 | 4.304000000E-06 | 4.765600000E-05 |
Table 3: Comparison of the New Hybrid Block Method with Block Method (Kuboye, 2015), Block Hybrid Backward Difference Formula (Mohammed & Adeniyi, 2014) and Block Method (Mohammed, 2011) for Solving Problem 3.
Conclusion
The derivation of block method with three generalised hybrid points through interpolation and collocation approach for solving second order initial value problems of ODEs has been examined in this paper. In order to compare the new developed method with the existing ones, a specific hybrid point was selected and the results generated compared favourably with existing methods in terms of accuracy. These are evidently shown in Tables 1-3.
References
- Lambert JD (1973) Computational Methods in Ordinary Differential Equations. Introductory Mathematics for Scientists and Engineers. Wiley Online Library.
- Fatunla SO (1988) Numerical Methods for Initial Value Problems in Ordinary Differential Equation. Academic Press Inc. Harcourt Brace Jovanovich Publishers, New York, USA.
- Brugnano L, Trigiante D (1998) Solving Differential Equations by Multistep Initial and Boundary Value Methods. CRC Press, USA.
- Awoyemi DO (2001) A new sixth-order algorithm for general second order ordinary differential equations. Int J Comput Math 77: 117-124.
- Jator SN (2007) A sixth order linear multistep method for the direct solution of y"= f (x, y, y'). Int J Pure Appl Math 40: 457- 472.
- Kayode SJ, Adeyeye O (2011) A 3-Step Hybrid Methods for Direct Solution of Second Order Initial Value Problems. Aust Basic Applied Sci 5: 2121-2126.
- Odejide SA, Adeniran AO (2012) A Hybrid linear collocation multistep scheme for solving first order initial value problems. J Nigerian Math Soc 31: 229-241.
- Sagir AM (2013) An accurate computation of block hybrid method for solving stiff ordinary differential equations. World Acad Sci Eng Technol 76: 384-387.
- Yap KY, Ismail F, Senu N (2014) An accurate block hybrid collocation method for third order ordinary differential equations. J Appl Math 1-9.
- Awari YS, Abada AA (2014) A Class of Seven Point Zero Stable Continuous Block Method for Solution of Second Order Ordinary Differential Equation. IJMSI 2: 47-54.
- Awari YS, Chima EE, Kamoh NM, Oladele FL (2014) A Family of Implicit Uniformly Accurate Order Block Integrators for the Solution of y" = f (x,y,y’). IJMSI 2: 33-46.
- Adeniyi RB, Alabi M (2011) A collocation method for direct numerical integration of initial value problems in higher order ordinary differential equations. Alexandru Ioan Cuza 57: 311-321.
- Kuboye JO (2015) Block methods for solving higher order ordinary differential equations directly using interpolation and collocation approach. Universiti Utara Malaysia.
- Mohammed U, Adeniyi RB (2014) Derivation of Five Step Block Hybrid Backward Differential Formulas (HBDF) through the Continuous Multi-Step Collocation for Solving Second Order Differential Equation. Pac J Sci Technol 15: 89-95.
- Mohammed U (2011) A class of implicit five-step block method for general second order ordinary differential equations. JNMS 30: 25-39.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi 