Editorial, Res Rep Math Vol: 2 Issue: 2

Mathematical Analysis of the Concept equality

Burgin M^*

Technical University of Moldova, Moldova

*Corresponding Author : Burgin M
Department of Mathematics, University of California, 405 Hilgard Ave., Los Angeles, CA 90095, USA
Tel: (818) 817 3170
E-mail: mburgin@math.ucla.edu

Received: April 04, 2018 Accepted: April 04, 2018 Published: April 12, 2018

Citation: Burgin M (2018) Mathematical Analysis of the Concept equality. Res Rep Math 2:2

Abstract

Keywords: Equality; Logic; System; Identity; Equivalence; Hierarchy; Relativity

Introduction

Metamathematics studies formalized mathematical theories and tools used for building these theories. One of the basic tools utilized in construction of mathematical and logical theories is equality. Although the notion of equality has existed from ancient times, the mathematical sign = denoting equality was introduced by the Welsh physician and mathematician Robert Recorde [1].

Much later Gottlob Frege methodically explained the difficulties posed by the notion of equality [2]. Importance of the notion of equality is also stressed by contemporary mathematicians and logicians; cf., for example, Church, 1956; Kleene, 1967; Kauffman, 1995; 1999; Homotopy Type Theory [3-7].

That is why different mathematicians and logicians have investigated properties of equality trying to achieve more clarity and precision. In spite of their efforts, equality puzzle persists without consensus on any solution [8].

Looking rather simple and intuitive, the concept of equality demands more considerations than it is usually done because what seems equal from some point of view can look very different from another. For instance, all letters a printed on a piece of paper are equal as symbols of an alphabet, i.e., from the linguistic perspective. However, the same letters are different as physical objects being situated at different places on the paper.

These considerations bring us to the idea of equality relativity meaning what is equal from one point of view or in one situation can be not equal from another point of view or in another situation. This idea already appears in the dialogue Phaedo of Plato where Socrates asks:

Is it not true that equal stones and sticks sometimes, without changing in themselves, appear equal to one person and unequal to another? [9]

However, explaining relativity and subjective comprehension of equality of things, Socrates suggests representing the approach of Plato:

We admit, I suppose, that there is such a thing as equality - not the equality of stick to stick and stone to stone, and so on, but something beyond all that and distinct from it - absolute equality. [9]

Later philosophers, logicians and mathematicians started investigating the concept of equality trying to find an adequate definition for this pervasive structure. Works of different researcher in this area is presented in Section 2 of this paper. After this, to solve the problem of finding an adequate definition of equality, we suggest three innovations - the identification hierarchy, which is considered in Section 3, as well as multifaceted scheme and formalized relativistic approach used for the development of the multifaceted relativistic theory of equality, elements of which are presented in Section 4. Note that we suggest relativity of the general concept of equality while Plato spoke about relativity of equality comprehension. The relativistic approach formalized in Section 4 involves three basic – predicative, semiotic and systemic – and several other forms of equality, properties of which are explored. Section 5 studies algorithmic properties of equality such as decidability and computability. Section 6 contains concluding remarks and a summary of the main results.

Investigations of Equality in Logic, Mathematics and Philosophy

The modern understanding of intensional issues and problems with equality was originated by Gottlob Frege in his fundamental paper [2]. This paper opens with a presentation of the difficulties caused by the notion of equality. In his earlier work, Frege also explained that equality he studied was related to names, or signs, of objects, and not to objects themselves [10]. Note that according to named set theory, a description, definition or portrayal of an object is a name of this object [11]. Thus, Frege studied equality of names relating them to objects they designate.

In his studies of equality, Frege treated equality as a proposition and genuinely assumed that the proposition a = b is true if and only if the object with the name a is identical to the object with the name b. For instance, the proposition 1 + 1 = 2 is true if and only if the number 1 + 1 just is the number 2. And the equality” Mark Twain is Samuel Clemens” is true if and only if the person Mark Twain just is the person Samuel Clemens.

However, Frege noticed that the proposition a = a has a cognitive significance (or meaning) that must be different from the cognitive significance of the proposition a = b. Indeed it is possible to learn that “Mark Twain is Mark Twain” is true simply by inspecting it, but it is impossible to learn the truth of the proposition “Mark Twain is Samuel Clemens” simply by inspecting it. Indeed, it is necessary to have additional information to see whether the two persons are the same. Besides, the first of these equalities “Mark Twain = Mark Twain” does not give us information while the second one “Mark Twain = Samuel Clemens” informs us what was the real name of the famous writer Mark Twain.

In logics and semiotics, meanings related to terms or names are often called intensions while things designated by these terms or names are specified as extensions. Consequently, contexts in which extension is all that matters are called extensional, while contexts in which extension is not enough are identified as intensional. In mathematics, equality is typically extensional. For instance, the equality 1 + 8 = 5 + 3 is true in the conventional Diophantine arithmetic even though the two terms involved may differ in meaning when the knowledge of small children is involved. This demonstrates that mathematical pedagogy differs from mathematics as a science.

Hilbert and Bernays introduced and studied deductive equality of formulas in logics. Namely, formulas A and B are deductively equal in a logic L if A can be deduced from B and B can be deduced from A in the logic L [12].

Traditionally logicians studied equality in three forms – as a binary relation in a set (class), as a binary predicate/proposition on pairs of elements from a set (class), and as a characteristic function or indicator function identifying those pair elements of which are equal. Recently, a new homotopic approach to equality was suggested in homotopy type theory by treating equality as the type IdA (a, b) or a = b representing the proposition of equality between a and b. As the basic structure in homotopy type theory is the path, the type a = b is the type of all paths from the object a to the object b. In a formal theory, objects are propositions and a path from the object a to the object b is interpreted as a proof that a proposition a is equal a proposition b. In homotopy type theory, a type IdA is treated as a space and a proof of the equality a = b is interpreted as a path between a and b [7].

Properties of paths allow getting properties of equalities such as reflexivity, symmetry and transitivity. Indeed, for any object a, there exists a path of type a = a, corresponding to the reflexive property of equality. The symmetric property of equality follows from the property of paths stating that a path of type a = b can be inverted, forming a path of type b = a. The symmetric property of equality follows from the property of paths stating that two paths of type a = b and b = c can be concatenated.

Note that in a type theory, all objects, e.g., sets or their elements, have types. This makes such objects named sets or fundamental triads [11]. Moreover, homotopy is a continuous transformation (say, f) of one topological object A or a function into another B. Consequently, homotopy is a named set (fundamental triad) of the form (A, f, B). Homotopy Type Theory is used as Univalent Foundations of mathematics [7]. Thus, Univalent Foundations of mathematics are based on named sets demonstrating once more that named set theory forms the unified foundations of mathematics [13].

Identification Hierarchy and Axioms of Equality

To solve the problem of finding an adequate definition of equality, we suggest three innovations - the identification hierarchy, which is considered in this section, as well as multifaceted scheme and relativistic approach used for the development of the relativistic theory of equality, elements of which are presented in the next section.

Thus, to better understand equality, we introduce the identification hierarchy with three levels of connections between objects going from the strongest to the weakest:

1. Identity determines when it is the same object is comprehended in different observations. Identity is denoted by a ≡ a.

2. Equality determines when it is possible to consider (treat) two objects as the same. Equality is denoted by a = b.

3. Equivalence determines when it is possible to consider (treat) two objects as interchangeable (in some situations). Equivalence is denoted by a ≈ d.

It is necessary to remark that in literature in general and even in mathematical publications, the terms equality and identity are used interchangeably (cf., for example, [8,14]. Besides, the terms equality and equivalence are also often used interchangeably although in some contexts, equality is sharply distinguished from equivalence or isomorphism.

To be able to define these terms in an exact fashion, it is necessary to discern identity, equality and equivalence in logic, as well as in mathematical and scientific contexts.

Equivalence or the equivalence relation on a set is defined axiomatically by three properties -reflexivity, symmetry, and transitivity. Namely, a binary relation Q on X is equivalence if it satisfies the following axioms:

E1. Q is reflexive, i.e. xQx for all x from X.

E2. Q is symmetric, i.e., xQy implies yQx for all x and y from X.

E2. Q is transitive, i.e., xQy and yQz imply xQz for all x, y, z ∈ X.

There are different kinds of the equivalence relation.

In algebra, the major equivalence is called isomorphism. Namely, two algebraic systems A and B are isomorphic if there is a one-to-one mapping between elements of A and B such that it and its inverse preserve algebraic operations.

In topology, the major equivalence is called homeomorphism. Namely, two topological spaces A and B are homeomorphic if there is a one-to-one mapping between elements of A and B such that it and its inverse are continuous.

In set theory, the major equivalence is called equipotence. Namely, two sets X and Y are equipotent if there is a one-to-one correspondence between X and Y (cf. Appendix)

In geometry, the major equivalence is called isometry. Namely, two geometric objects A and B are isometric if there is a one-to-one mapping between elements of A and B such that it and its inverse preserve distances.

Remark 3.1. In algebra equality with variables are often called identities. For instance,

x + y = y + x

is the commutativity identity.

Giuseppe Peano was a very active researcher authorizing more than 200 books and papers, becoming of the founders of mathematical logic and essentially developing logical notation. As a part of his research, Peano suggested the most popular axiomatic system for the conventional Diophantine arithmetic [15]. This system also included axioms for equality, which usually are presented in the following form:

x = x

x = y ⇔ y = x

x = y & y = z ⇒ x = z

x = y ⇒ (A(x) ⇒ A(y))

These axioms represent the concept of predicative equality and are consistent and independent (cf., for example, (Church, 1956)) [3]. In contemporary expositions, the fourth axiom is usually presented by two axioms (cf., for example, (Rasiowa and Sikorski, 1963)) [16]:

x₁ = y₁ & x₂ = y₂ & … & x_n = y_n ⇒ (F(x₁ , x₂ , … , x_n) ⇒ F(y₁ , y₂ , … , y_n))

x₁ = y₁ & x₂ = y₂ & … & x_n = y_n ⇒ (P(x₁ , x₂ , … , x_n) ⇒ P(y₁ , y₂ , … , y_n))

Here F is an arbitrary function with n arguments and P is an arbitrary binary predicate with n arguments.

Logicians build a formal first-order theory of pure equality, the signature of which consists of the equality relation symbol = and which does not include non-logical axioms [17]. This theory is consistent because any set with the usual equality relation provides its interpretation. Lowenheim proved decidability of the first-order theory of pure equality [18]. By adding either the axiom saying that for a fixed natural number m, there are exactly m objects in the considered set, or an axiom scheme stating that the set is infinite, the theory of pure equality is made complete.

Varieties of Equality

To describe existing forms of equality, we assume that identity of objects is already, i.e., a priory, defined for elements of a chosen set. In each case, a specific set is chosen, in which it is possible to uniquely identify objects, i.e., to find when what seems to be two objects is in essence one and the same object.

Predicative equality originated from the proposal of Leibniz, who characterized equality in the following way [19]:

Given any objects a and b, the equality a = b is true if and only if, given any predicate P, we have P(a) if and only if P(b).

However, the definition contains the vicious circle because to define the equality a = b, the definition uses the equality P(a) = P(b) or the equalities P(a) is true and P(b) is true. Besides, the condition that includes any predicate P is not constructive. We remedy these shortcomings by making the definition relative and grounding it on the concept of identity, which is assumed already defined for the range of the predicates.

Thus, to define predicative equality, let us consider a class R of objects and a set P of predicates that take values in a set C, for elements of which identity is defined. Classical predicates take values in the set {True, False} or {1, 0}.

Definition 4.1. Two objects a and b from R are P-equal, i.e., equalwith respect to P, if for any predicate P(x) from P, the values P(a) and P(b) are the same (identical).

We denote it a =_P b.

Note that the scale of the predicates in P is not always {True, False} because P can contain predicates from a multivalued logic. Moreover, predicates are special cases of abstract properties (Burgin, 1985; 1986). That is why it is possible to define predicative equality using abstract properties instead of predicates [20,21].

Example 4.1. If we have a mapping f: X → Y, then the equality f(x) = y implies that for any predicate P(a) defined for elements from Y, P(f(x)) is identical to (the same as) P(y).

Example 4.2. In ZF-axiomatic theory of sets, there are two approaches to defining equality of sets in the class Set of all sets [22,23]:

(Intensional equality) ∀x and y ( x = y if ∀z (x ∈ z if and only if y ∈ z))

(Extensional equality) ∀x and y ( x = y if ∀z (z ∈ x if and only if z ∈ y))

Intensional equality is a predicative equality defined by the system of predicates P_I = {P_z(x)} of the form x ∈ z.

Extensional equality is a predicative equality defined by the system of predicates P_E = {Q_z(x)} of the form z ∈ x.

Note that extensional equality is based on the inner structure of a set while intensional equality is based on the outer structure of a set [24].

Lemma 4.1. Predicative equality is an equivalence relation on R.

Proof. According to the properties of equivalence relation (cf. Section 3), we have to check that the relation =_P is reflexive, symmetric and transitive.

Reflexivity. Indeed, for any object a and any system P of predicates and any predicate P, we have P(a) = P(a) implying a =_P a.

Symmetry. Indeed, for any system P of predicates and any predicate P, we have if P(a) = P(b), then P(b) = P(a) and thus, a =_P b implies b =_P a.

Transitivity. Let us assume that for some objects a, b and c from R, we have a =_Pb and b =_P c. It means that for any predicate P from P, we have P(a) = P(b) and P(b) = P(c). As identity is a transitive relation, we obtain P(a) = P(b). Consequently, P(a) = P(c) and thus, a =_Pc.

Lemma is proved.

It is possible to find a more formalized proof of this result in (Kleene, 1967) [4].

To define semiotic equality, let us consider a semantic function (mapping) S: R → M defined for the class R of objects and having the field of meanings M, for elements of which identity is defined.

Definition 4.2. Two objects a and b from R are S-equal, i.e., equalwith respect to the semantics S, if S(a) = S(b).

We denote it a =_S b.

Example 4.2. Let take a class R, which consists of texts while the semantic S assigns meaning to the texts. Then to texts are semantically equal if they have the same meaning.

Lemma 4.2. Semiotic equality is an equivalence relation on R.

Proof is similar to the proof of Lemma 4.1.

A particular case of semiotic equality is nominalistic equality. It is defined for objects that play the role of names for other objects. That is, the class R consists of names of objects from the set M.

Definition 4.3. Two names a and b from R are nominalistically equal if they are names of the same object from M.

We denote it a =_M b.

Logicians often like to consider the following example.

Example 4.3. Logicians often like to consider the following example suggested by Frege [2].

The morning star is equal to the evening star. (1)

For a long time, people saw a bright star in the morning and a bright star in the evening. For instance, ancient Egyptians and Greeks believed that those were actually two separate objects, a morning star and an evening star. Consequently, ancient Greeks called the morning star Phosphoros, which meant the bringer of light, while they called the evening star Hesperos, which meant the star of the evening. When astronomers started their observations, they found that the names “the morning star” and “the evening star” both designate the planet Venus. Thus, equality (1) means that “the morning star” and “the evening star” are names of the same physical object.

So, why one object had in some sense opposite names? The cause is that the orbit of the Venus is inside the orbit of the Earth. As a result, the Venus is always relatively close to the Sun in the sky. Thus, when the Venus is on one side of the Sun, it is following the Sun in the sky and comes into view soon after the Sun sets, while the sky is already dark enough for it to be observable. Thus, the Venus is at its brightest only minutes after the Sun disappears implying that the Venus is the evening “star.”

However, being on the other side of the Sun, the Venus go in front of the Sun as it travels across the sky. In particular, the Venus rises in the morning a few hours before the Sun and when the Sun rises, the sky brightens and the Venus disappears gradually in the daytime sky, which implies that the Venus the morning “star.”

In this context, the morning star and the evening star are the same in one way and not the same in another (cf., for example, (Fitting, 2015)). Indeed, the terms “the morning star” and “the evening star” convey different information about the planet Venus and thus, have different meaning.

Lemma 4.3. Nominalistic equality is an equivalence relation on R.

Proof is similar to the proof of Lemma 4.1.

To define systemic equality, let us consider a class R of objects and a class of systems K.

Definition 4.4. Two objects a and b from R are equal with respect to K or K-equal if for any system A from K in which a is its element (component or part), substitution of some of objects a by objects b in A does not change this system A and for any system B from K in which b is its element (component or part), substitution of some of objects b by objects a in B does not change this system B.

We denote it a =_K b.

Example 4.4. In the world “alphabet”, the first letter a is equal to the second letter a because it is possible to change one for another without changing the word “alphabet”. In this case, the system K consists of words and two physical symbols (letters) are K-equal if any word stays the same after we change one of them by another one.

Lemma 4.4. Systemic equality is an equivalence relation on R.

Proof is similar to the proof of Lemma 4.1.

Note that systemic equality assumes that objects from R can be elements (components or parts) of systems K. However, if all objects from R cannot be elements (components or parts) of systems K, then all elements from R are equal with respect to K because by properties of predicative reasoning, any two objects from R that cannot be elements (components or parts) of systems K are equal with respect to K.

It is also possible to introduce linguistic equality as a specific kind of systemic equality taking texts as systems and words as objects.

Let us consider a set W of words and a set of texts T. Note that it is possible to consider any situation or system as a text (in some generalized way) and objects as words from such generalized texts.

Definition 4.5. Two words v and u from W are equal with respect to T or T-equal if for any text A from T in which v is its element, substitution of v by u in A does not change the meaning of text A and for any text B from K in which u is its element, substitution of u by v in B does not change the meaning of text B.

We denote it a =_T b.

Lemma 4.5. Linguistic equality is an equivalence relation on R.

Proof is similar to the proof of Lemma 4.1.

It is possible to demonstrate that all these concepts of equality are reducible to one another, i.e., they are equivalent.

Let us consider a class R of objects. Then it is also possible to represent P–equality by S–equality.

Theorem 4.1. For any semantics S: R → M, there is a system P of binary predicates such that any two objects a and b from R are S-equal if and only if they are P–equal.

Proof. Let us consider a semantics S: R → M. For each element m from M, we build the following predicate on the class R:

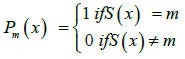
and define P = { P_m(x); m ∈ M}. Then for any objects a and b from R, S(a) = S(b) if and only if P_m(a) = P_m(b) for all m ∈ M. It means that a and b are S-equal if and only if they are P–equal.

Theorem is proved.

It is also possible to represent S–equality by P–equality.

Theorem 4.2. For any system P of predicates, there is a semantics S: R → M such that any two objects a and b from R are P-equal if and only if they are S–equal.

Proof. Let us consider a set P of predicates P_i with the scale C_i of its values (i ∈ I). Note that all scales C_i can coincide. For instance, they all can be equal to the set {True, False}.

We define the set M equal to the Cartesian product and semantics S: R → M by the rule

S(a) = (P_i (a); i ∈ I)

Then for any objects a and b from the class R, S(a) = S(b) if and only if P_i(a) = P_i(b) for all i ∈ I. It means that a and b are S-equal if and only if they are P–equal.

In such a way, we build the necessary logical semantics.

Theorem is proved.

Additionally it is possible to represent P–equality by K–equality.

Theorem 4.3. For any set P of predicates, there is a set K of systems such that any two objects a and b from the class R are P-equal if and only if they are K-equal.

Proof. Let us consider a set P of predicates P_i(x) with the scale C_i of its values (i ∈ I). Note that all scales C_i can coincide. For instance, all of scales can be equal to the set {True, False}. Each predicate P_i(x) is an abstract system and x is an element of this system. Thus, we can take K equal to {(P_i(x), P_i(a)); a ∈ R, i ∈ I } where Pi(a) is the value of for the element a. Then a and b are K-equal if and only if they are P–equal because both in the case of P-equality and the case of K-equal, a = b if and only if P_i(a) = P_i(b) for all i ∈ I.

Theorem is proved.

In addition it is possible to represent S–equality by K–equality.

Theorem 4.4. For any set K of systems, there is a semantics S: R → M such that any two objects a and b from R are S-equal if and only if they are K–equal.

Proof. Let us consider a set K of systems, a class (set) M equal to the set 2^R of all subsets of R and build semantics S: R → M by the following rule.

S(a) = { bi ; a =_K bi }

Note that any object a from R belongs to S(a) because by Lemma 4.1, =_K is an equivalence relation.

Then for any objects a and b from R, S(a) = S(b) if and only if a =_K b. Consequently, objects a and b are S-equal if and only if they are K–equal.

Theorem is proved.

Furthermore it is possible to represent K–equality by P–equality.

Theorem 4.5. For any set K of systems, there is a system P of binary predicates such that any two objects a and b from R are K-equal if and only if they are P–equal.

Proof. Let us consider a set K of systems. Then by Theorem 4.4, there is a semantics S: R → M such that any two objects a and b from R are S-equal if and only if they are K–equal. In addition, by Theorem 4.1, there is a system P of binary predicates such that any two objects a and b from R are S-equal if and only if they are P–equal. Consequently, any two objects a and b from R are K-equal if and only if they are P–equal.

Theorem is proved.

Finally it is possible to represent S–equality by K–equality.

Theorem 4.6. For any semantics S: R → M, there is a set K of systems such that any two objects a and b from the class R are S-equal if and only if they are K–equal.

Proof. Let us consider a semantics S: R → M. Then by Theorem 4.1, there is a system P of binary predicates such that any two objects a and b from R are S-equal if and only if they are P–equal. At the same time, by Theorem 4.3, there is a set K of systems such that any two objects a and b from the class R are P-equal if and only if they are K-equal. Consequently, any two objects a and b from R are K-equal if and only if they are S–equal.

Theorem is proved.

Homotopy type equality was introduced by Voevodsky and studied in homotopy type theory [7]. There are also: transportational equality, substitutional equality and judgmental or definitional equality. In addition, there are higher equalities in homotopy type theory [25].

Philosophers and logicians tried to characterize a unique absolute equality. Even Plato discussed a unique absolute idea, or structure in contemporary understanding [7], of equality in general [30]. However, relativity of equality considered above shows that there is a variety of different types and forms of equality. To organize this variety in a structured system, we additionally introduce modalities of equality. There are several types of such modalities.

Existential modalities of equality

1. Tentative (potential) equality is not completely established.

2. Existing (situational) equality is completely established but depends on the situation – in one situation it is true, while in another it is false.

3. Imperative (necessary) equality is always true.

Here are some examples:

The statement “” expresses potential equality.

The expression “2 + 2 = 4” expresses situational equality because it is true in the conventional Diophantine arithmetic but is not true in some non-Diophantine arithmetics [26,27].

The expression “3 = 3” expresses imperative equality.

Inclusive modalities of equality

1. Relative equality is equality that depends on its context.

2. Absolute in a class (invariant) equality is equality that is invariant in the given class.

3. Absolute equality is equality that is invariant in general.

For instance, the equality 2 + 2 = 4 is relative in the class of all arithmetics but is absolute in conventional Diophantine arithmetic, while the equality 3 = 3 is absolute.

Temporal modalities of equality

1. Static equality is equality between two unchanging objects.

2. Dynamic equality is equality between two changing objects.

3. Evolutionary equality is equality between two developing objects.

For instance, equality 2 + 2 = 4 is static in conventional Diophantine arithmetic. Equality between you today and you yesterday is dynamic. Equality between you as a child and you as an adult is evolutionary.

Modalities of equality are complemented by roles of equality. It is possible to discern three basic roles:

1. Equality plays the definitive role when one side of it (usually, right) is known while the other side (usually, left) is unknown and defined by the first (right) side.

2. Equality plays the equivalizing role when both sides of it are known and they are treated as the same.

3. Equality plays the reduction role when both sides of it are known and equality shows that it is possible to use one side instead of the other one.

Here are some examples. When we say “arithmetic is a science of numbers,” it is equality in the definitive role. Equality 2 + 2 = 4 is in the equivalizing role. Equality ²/â�?�? = ½ is plays the reduction role demonstrating how the fraction ²/â�?�? is reduced to the fraction ½ .

Equality is also classified by the domain where it is applied. People have discussed and studied:

• Political equality means that all have equal voice in making laws and selecting political leaders

• Social equality means that all have equal access to those things necessary to leading a decent or good life

• Moral equality means for all equal human value or worth

• Legal equality means that all are subject to the same laws

• Linguistic equality is equality of languages [28].

• Logical equality is an operation on two logical values.

Here we do not analyze these particular types of equality as our main concern is the general concept of equality.

Algorithmic Properties of Equality

Basic algorithmic properties are decidability, recognizability and computability [29,30]. We remind their definitions for binary relations in a set X.

Definition 5.1. A binary relation R in X is decidable in a class A of algorithms if there is an algorithm A in A such that for any elements objects a and b from X, the algorithm A decides whether the pair (a, b) belongs to R or does not belong.

Definition 5.2. A binary relation R in X is recognizable in a class A of algorithms if there is an algorithm A in A such that for any elements objects a and b from X, the algorithm A informs when the pair (a, b) belongs to R.

Definition 5.3. A binary relation R in X is computable in a class A of algorithms if there is an algorithm A in A such that for any elements objects a and b from X, the algorithm A computes all pairs (a, b) that belong to R.

For many classes of algorithms, e.g., for Turing machines, recognizability and computability coincide [30]. For some classes of algorithms, e.g., for finite automata, recognizability and decidability coincide [29].

Algorithmic properties of equality are represented by algorithmic modalities of equality

Decidable (subrecursively, recursively, inductively) equality

Undecidable equality

Computable, recognizable or identifiable (subrecursively, recursively, inductively) equality

Noncomputable/non-recognizable equality

Algorithmic modalities of equality depend on the selected type or class of algorithms, i.e., these modalities are relative. There are three basic types of algorithms [31]:

Subrecursive algorithms

Recursive algorithms

Inductive algorithms

As a result, each algorithmic modality has three subclasses. Namely, decidable can mean - subrecursively, recursively or inductively decidable while undecidable can mean - subrecursively, recursively or inductively undecidable. In a similar way, computable/ recognizable can mean - subrecursively, recursively or inductively computable/recognizable while noncomputable/non-recognizable can mean - subrecursively, recursively or inductively noncomputable/ non-recognizable.

It is easy to show by induction, that equality of two arithmetical expressions, i.e., expressions built from numbers using arithmetical operations, in the conventional Diophantine arithmetic is recursively decidable, i.e., decidable in a class of recursive algorithms such as Turing machines. At the same time, the first Gödel undecidability theorem shows that equality of two logical expressions in the language of the first-order arithmetic is recursively undecidable [32].

In a similar way, equality of real numbers defined by formulas that involve the integers, the basic arithmetic operations, the logarithm and the exponential function is recursively undecidable.

However, it is proved that any arithmetical relation including equality of two logical expressions in the language of the first-order arithmetic is inductively decidable, namely, they are decidable by algorithms from the constructive inductive hierarchy [31]. At the same time, equality of different systems is decidable on different levels of this hierarchy. For instance, equality of words in recursively enumerable languages is decidable on the first level while equality of recursively enumerable languages is decidable only on the second level [33].

Algorithmic properties of equality are very important in algebra, for example, Birget et al. [34]. In turn, the problem of deducibility of relations in associative calculi, the homeomorphism problem for topological manifolds and the homotopy equivalence problem in finite-dimensional manifolds are equivalent to algorithmic problems, namely, to the word problem for finitely presented semigroups and groups and the isomorphism and conjugacy problems for finitely presented groups. In particular, the word problem is a problem of equality of two words defining elements of a factor algebra of a free semigroup or group [35].

It is proved that the word problem is recursively undecidable for semigroups and groups [34]. Consequently, equality in semigroups and groups is also recursively undecidable.

Conclusion

To construct an adequate definition of equality in this paper, we suggested three innovations - the identification hierarchy, multifaceted scheme and relativistic approach. Based on this methodology, the concept equality was explored utilizing the hierarchy of identification relations used in mathematics and other fields. This hierarchy consists of three levels – identity, equality and equivalence. Correct definition and utilization of these concepts demands clear differentiation of them in logic, as well as in mathematical and scientific contexts.

It was demonstrated that equality is a relative relation, which depended on the used perspective and occupying the middle position in the hierarchy of identification relations. Following this approach, it was demonstrates how it was possible to introduce and discern different types and forms of equality the most basic of which were logical, semiotic and systemic equalities. Various properties of equality were obtained including modalities and algorithmic properties.

References

1. Recorde R (1557) Arithmetike: containyng the extraction of Rootes: The Coßike practise, with the rule of Equation and the woorkes of Surde Nombers, Jhon Kyngstone, London, UK.
2. Frege G (1892) Über Sinn und Bedutung, Zeitschrift für Philosophie und philosophische Kritik.
3. Church A (1956) Introduction to Mathematical Logic, Princeton University Press, Princeton, USA.
4. Kleene SC (1967) Mathematical Logic, John Wiley & Sons, New York, USA.
5. Kauffman LH (1995) Arithmetic in the Form, Cybernetics and Systems 26: 1-57.
6. Kauffman LH (1999) What is a Number? Cybernetics and Systems 30: 113-130.
7. Program TU (2013) Homotopy Type Theory: Univalent Foundations of Mathematics. arXiv preprint.
8. Parsons T (2000) Indeterminate identity: Metaphysics and Semantics, Clarendon Press, Oxford, UK.
9. Hamilton E, Cairns H (1961) The collected dialogues of Plato. Princeton University Press, New Jersey, USA.
10. Frege G (1879) Begriffsschrift, eine der arithmetischen nachgebildete Formalsprache des reinen Denkens, L. Nebert, Halle, Germany.
11. Burgin M (2011) Theory of Named Sets, Mathematics Research Developments, Nova Science Publishers, New York,USA.
12. Hilbert D, Bernays P (1968) Die Grundlagen der Mathematik I, Springer-Verlag, New York, USA.
13. Burgin M (2004) Unified Foundations of Mathematics, arXiv preprint.
14. Feferman S (1974) The Number Systems: Foundations of Algebra and Analysis, Addison-Wesley, Reading, Massachusetts, USA.
15. Peano G (1889) Arithmetices principia nova method exposita, Bocca, Torino.
16. Rasiowa H, Sikorski R (1963) The Mathematics of Metamathematics, Panswowe Wydawnictwo Naukowe, Wraszawa, Poland.
17. Monk JD (1976) Mathematical Logic, Graduate Texts in Mathematics, Springer-Verlag, New York, USA.
18. Löwenheim L (1915) Über Möglichkeiten im Relativkalkül. Mathematische Annalen 76: 447-470.
19. Blok WJ, Pigozzi D (1989) Algebraizable logics. American Mathematical Soc 77: 78.
20. Burgin M (1985) Abstract theory of properties, Non-classical Logics, Institute of Philosophy, Moscow, Russia.
21. Burgin M (1986) Quantifiers in the Theory of Properties, Nonstandard Semantics of Non-classical Logics, Institute of Philosophy, Moscow, Russia.
22. Fraenkel AA, Bar-Hillel Y (1958) Foundations of Set Theory, North Holland PC, Amsterdam, Netherlands.
23. Kuratowski K, Mostowski A (1967) Set Theory, North Holland PC, Amsterdam, Netherlands.
24. Burgin M (2017) Ideas of Plato in the context of contemporary science and mathematics. Athens Journal of Humanities and Arts 4: 161-182.
25. Shulman M (2016) Homotopy Type Theory: A synthetic approach to higher equalities.
26. Burgin M (1997) Non-Diophantine Arithmetics or what number is 2+2? Ukrainian Academy of Information Sciences, Kiev, Ukraine.
27. Burgin M (2007) Elements of Non-Diophantine Arithmetics, 6th Annual International Conference on Statistics, Mathematics and Related Fields, Honolulu, Hawaii.
28. Griffiths P (1990) Equality in language: Aspects of the theory of linguistic equality, Durham theses, Durham University, England.
29. Sipser M (1997) Introduction to the Theory of Computation, PWS Publishing Co, Boston, USA.
30. Burgin M (2010) Measuring Power of Algorithms, Computer Programs, and Information Automata, Nova Science Publishers, New York, USA.
31. Burgin M (2005) Super-recursive Algorithms, Springer, New York, USA.
32. Gödel K (1931) Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. Monatshefte für mathematik und physik 38: 173-198.
33. Burgin M (2010) Algorithmic Complexity of Computational Problems. Int J Comput Info Tech 2: 149-187.
34. Birget JC, Margolis S, Meakin J, Sapir MV (2000) Algorithmic problems in groups and semigroups. Springer Science & Business Media, USA.
35. Waszkiewicz W (1971) The notions of isomorphism and identity for many-valued relational structures. Studia Logica 27: 93-98.