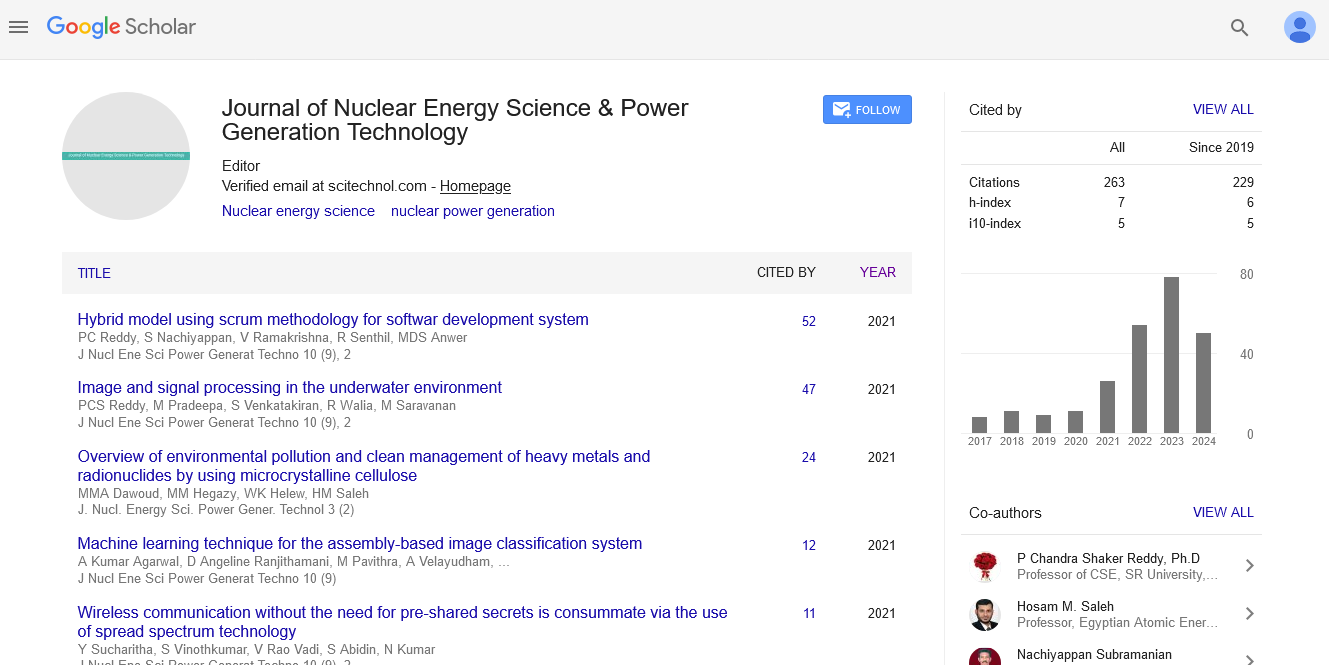
Research Article, J Nucl Ene Sci Power Generat Technol Vol: 6 Issue: 1
On Electrochemical Maintaining of the Given Quality of Molten Salt Reactors
| Pavel N Alekseev and Alexander L Shimkevich* | |
| NRC Kurchatov Institute, Moscow, Russia | |
| Corresponding author : Alexander L Shimkevich NRC Kurchatov Institute, 1, Kurchatov Sq., Moscow, 123182, Russia E-mail: shimkevich_al@nrcki.ru |
|
| Received: July 12, 2016 Accepted: December 27, 2016 Published: January 02, 2017 | |
| Citation: Alekseev PN, Shimkevich AL. (2017) On Electrochemical Maintaining of the Given Quality of Molten Salt Reactors. J Nucl Ene Sci Power Generat Technol 6:1. doi:10.4172/2325-9809.1000163 |
Abstract
A concept for electrochemical maintaining of the given quality of a fuel composition of molten-salt reactor (MSR) is formulated. The correction of molten-salt properties can be carried out with the help of a forced and controllable variation of Reduction–Oxidation (RedOx) potential of any liquid salt mixture by changing its little non-stoichiometry. For this, electronic properties of molten fluorides are studied and optimal managing basic compositions of MSR is offered in using the strong electron influence of molten fluorides on liquidus morphology of these systems which is responsible for ionic and covalent bonds in them. The accent is made on managing the electrochemical potential (Fermi level) in the band-gap of nonstoichiometric molten fluorides by the precise coulomb-metric titration of alkali atoms in a galvanic cell with the solid electrolyte from A+–β”–Al2O3 where A is alkali metal (for example potassium) and liquid-lead working electrode.
Keywords: Electrochemical maintaining; Molten salt reactors; Quality
Keywords |
|
| Electrochemical maintaining; Molten salt reactors; Quality | |
Introduction |
|
| Despite of wide experience in studying molten salts for different applications, their microstructure, atomic dynamics, and electronic properties in the frame of band model have been not enough studied in a little non-stoichiometry of them not to mention an influence of their Reduction – Oxidation (RedOx) potential on structural, thermodynamic, physical, chemical, and corrosion properties of fuel compositions and coolants of molten-salt reactors (MSR) [1,2]. | |
| At the same time, studying the electronic properties of molten salts can be useful for providing a high-selective extraction of salt components, for minimizing a corrosion of structural materials in them, i.e. it can prove the reliable operation of molten salts in nonisothermal conditions [3,4]. | |
| Instead, the researchers have seen an important task for themselves in searching RedOx pairs suitable for keeping a given quality of fuel compositions and practical inhibiting their corrosion activity [5,6] whereas it is possible to deduce these characteristics from the nonstoichiometric state of salt as a crucial factor of its electrochemical potential as Fermi level in the band gap of salt in the frame of different microscopic models [1,7]. | |
| Indeed, the thermodynamic, physical, and chemical similarity of condensed matters takes place for the congruent forms of pair potentials [8]. Therefore, it is possible to deduce structural and chemical characteristics of any liquid salt as well as its phase diagram from its composition [1] and its non-stoichiometric state as an electrochemical potential [7]. | |
| In addition, it is practical to carry out a computation of molten salts as ionic melts by means of molecular dynamics (MD) [8] and quantum-mechanical studying the electron states of the condensed matter [9] to specify the kinds and forms of pair potentials for these MD simulations. Therefore, it is possible to develop a way for effective maintaining the given quality of molten salt from the analysis of its atomic-dynamic and electronic properties. | |
| In accenting the microscopic specificity of molten salts, it is easy to estimate an effect of salts dissociation on component solubility in the melt at changing its composition, to formulate approaches for developing a molten-salt technology. | |
Materials and Methods |
|
| An electronic-band model for molten salts | |
| Usually a RedOx pair is selected as a charged impurity (Mk+/M(k –1)+) suitable for keeping the given chemical quality of liquid salt by means of electrochemical reaction [6] for the required RedOx potential of molten salt which can be presented by equation. | |
 (1) |
|
 (2) |
|
| Or be transformed to the form | |
 (3) |
|
Here  is the standard potential of cationic pair,  , and  are the concentration of oxidizing  and reducing  ions of the metal impurity, M, of
variable valence in the salt, T is Kelvin temperature, R is gaseous
constant, and F is Faraday number. For multiple impurities dissolved
in the salt, Equation (1) should be presented in the common form: |
|
 (4) |
|
| Where, all the impurities Min should redistribute on their ionic states Mi ki+ and Mi (ki−1)+ so that their concentrations satisfy to equation [10]. | |
 (5) |
|
For each RedOx pair,  |
|
| At the same time, it is necessary taking into account a nonstoichiometry of the molten salt itself when its basic metal elements also participate in forming the resulting RedOx potential [10]. Then, the parameter, Etot, becomes an independent electrochemical variable and we can obtain the obvious concentration ratio for each RedOx pair from (5) | |
 (6) |
|
It is clear that the resulting RedOx potential, Etot, as a unified salt electrochemical potential is effectively stated by Fermi level, εF, in the
band gap of the liquid salt [3,4,10]. Then, the concentration,  ,
characterizes the electronic population of local energy state,  whose
total density in the salt is  and (6) is transformed to the form |
|
 (7) |
|
| Where, kB is Boltzmann constant. | |
Obviously, the difference between  and  is less the ratio
 is close to unity and vice versa. This is illustrated
by Figure 1 which shows the band structure of molten salt in two
cases when Fermi level is slightly above the impurity level, 
and it is essentially below the one. In the first case, the electron
population of impurity level,  is high high temperatures opposite to the second when
 according to (7). |
|
 |
Figure 1: The of electronic-band models of molten salt in two cases: (A) Fermi level, εF, (red line) is slightly above the impurity level, εMiKi+ (blue line segments); (B) the former is essentially below the latter; here “0” denotes a free-electron energy level, εc is the electron energy at the bottom of conduction band, εv is the electron energy at the top of valence band, εg is the energy band-gap of pure molten salt, solid line segments are the local energy levels occupied by electrons and the dotted ones are the vacant local levels (cations). |
One can see that even the some local energy levels of basic metals,
 , in the molten salt can contain electrons when the position
of Fermi level is sufficiently close to them (Figure 1A). These levels
occupied by electrons define of basic metals in the liquid salt as
uncharged atoms,  , whose concentration will not be equal to zero
 |
|
| The allowed local electron states in the band gap are formed in any molten dielectric compound due to Anderson’s localization of electrons in the “tails” of conduction and valence bands in an irregular lattice [11] which is illustrated by Figure 2 in comparing electronicband structures of crystalline and liquid compound having the broad band gap. | |
|
Figure 2: The band structure for stoichiometric crystalline salt: (A) with Fermi level, εFc, in the middle of band gap, εgc, and for hypo-stoichiometric (reduced) molten salt; (B) with Fermi level, εFr, being essentially higher the mid-gap, and the lesser band gap, εgm, due to existence (in the band gap) of allowed electron states near the bottom, εc, of conduction band as the basic cations, Mo+, and the ones near the top, εv, of valence band as the basic anions. |
It is clear that the solid salt in the stoichiometric state has Fermi
level in the middle of the band gap and its non-stoichiometric state
is possible only on the surface of the crystalline salt. Opposite, the
molten salt can easily change Fermi level in the bulk by dissolving one of the basic metals as uncharged atoms, in direct contact
with a liquid metal (indifferent for the salt) contained these atoms and
varying the ratio, , and  according to (7) [3,4,10]. |
|
In comparing Equations (6) and (7), it is possible to see t h a t Etot is equal to  and  is equal to  accurate within the some negative constant. For reduced molten salt  ,we obtain  at  from
(7), i.e. a portion of uncharged basic-metal atoms, , is equal to 10
ppm of its cations  in the molten salt when its RedOx potential,
Etot, is on 1 V more positive than its standard reduction potential, |
|
 |
|
Therefore, the concentration,  , of any uncharged reducer,
 , dissolved in the molten salt can be evaluated by the simple
formula [10,12] |
|
 (8) |
|
Where  is the concentration of the all cationic forms of
the impurity, Mi, in the salt. |
|
At the same time, the all components of molten salt have also the
covalent-bonding forms which decrease the concentration of their
cationic forms in the molten salt, i.e.  where CMi is the total
concentration of the impurity, Mi. |
|
| Thus, it is very important evaluating the portion of covalentbonding forms for basic molten salts in order to maintain their given quality by forced changing RedOx potential in direct contact with the liquid metal contained the given reducer. | |
| Phase-diagram features of fluoride systems | |
| It is known that any eutectic melting point, Тm, of any salt composition is always less than Тm of its components [13]. For example, the well known ternary system, KF–NaF–LiF, has the simplest morphology of liquidus surface shown in Figure 3 as a plot of its isotherms with eutectic breaks dividing the triangle of system composition into the areas for crystallizing the pure components denoted by the vertices of this triangle [14]. | |
|
Figure 3: The liquidus isotherms (thin lines in °С) of KF–NaF–LiF system and its eutectic breaks (thick lines) in the composition triangle with the components in the vertices [14]; the blue dotted line marks the mirror symmetry of the phase diagram. |
| One can see that each of the double eutectics: (KF)0.5(LiF)0.5 (Тm=492° С), (NaF)0.4(LiF)0.6 (Тm=652°С), and (KF)0.6(NaF)0.4 (Тm=710°С), is connected by almost straight lines (eutectic breaks) with the ternary eutectic (FLiNaK) at the composition of (KF)0.42(NaF)0.12(LiF)0.46 and Тm=454° С. The almost mirror symmetry of this phase-diagram projection as to the vertical line from the vertex, NaF, (blue dotted line in the composition triangle), apparently, is the effect of simplest liquidus morphology and the equality (with accuracy of 1%) of the LiF and KF melting points differing from Тm of NaF by 14% (Table 1) [3]. | |
|
Table 1: The melting point, Тm, of fluorides [13,14]. |
| The Figure 3 shows that there are no compounds in the system, KF–NaF–LiF, and solid phases of its components precipitate from the molten salt separately in the corresponding areas of composition triangle divided eutectic breaks. Then, one can expect that metallic phases of these components will separately precipitate from the reduced molten salt when they saturate the solution, i.e. at their thermodynamic activity defined by Henry law | |
 |
|
Where the concentration, , of the occupied-by-electrons level,
 , is defined by (8) as a function of Fermi level,  . The solubility,
 , of uncharged basic-metal atoms,  , in their molten salt is
very low conservative magnitude (<5 ppm) practically constant for
all metals [10]. Therefore, forced changing RedOx potential in direct
contact with the liquid metal will be confined by the basic-metal
component which has maximal  , i.e. minimal the covalentbonding
form. As pointed out below, such the component for FLiNaK
is potassium. |
|
| The mirror quasi-symmetry of phase diagrams is available also to a ternary system where two of its components are mutually solved both in solid, and in liquid state, for example, LiF–ThF4–UF4 and NaF–ThF4–UF4 [14,15]. In these fluorides, ThF4 and UF4, replace each other due to almost equal (with accuracy of 3%) ion radius, ri, of Th4+ and U4+ (Table 2). | |
|
Table 2: Energy of ionization, Ui, electronegativity, Ξ, work function, eϕ, radius of atom, ro, and an ion, ri, for fluorine and some metals [13,16,17]. |
| In Figure 4, one can see the phase-diagram projection of the ternary system, LiF–ThF4–UF4, in the composition triangle [14]. Two binary eutectics: (LiF)0.71(UF4)029(Tm=490°C) and (LiF)0.71(ThF4)0.29(Тm=565°C), will be connected by the straight line, (LiF)0.71[(UF4)1- x(ThF4)x]0.29 where 0 ≤ x ≤ 1 (red dotted line). In ignoring peritectic compositions of this system, we disclose its mirror symmetry as to a perpendicular (blue dotted line) from the vertex, LiF, on the opposite side of the system composition triangle. | |
|
Figure 4: The liquidus isotherms (thin lines in °С) of LiF–ThF4–UF4, its peritectics and eutectics (thick lines) in the composition triangle with the components in the vertices [14]; the red and blue dotted lines mark the mirror quasi-symmetry of the phase diagram. |
| Then, the difference in Figure 5 is expressed by only the simple shift of ternary-eutectic plot of NaF–ThF4–UF4 system to the line, (NaF)0.8[(UF4)1- x(ThF4)x]0.2 (red dotted line) that, most likely, is caused by the higher melting point of NaF (Table 1). | |
|
Figure 5: The liquidus isotherms (thin lines in °С) of NaF–ThF4–UF4, its peritectics and eutectics (thick lines) in the composition triangle with the components in the vertices [15]; the red and blue dotted lines mark the mirror quasi-symmetry of the phase diagram. |
| Homology series of excess phases in binary fluorides | |
| In comparing Figure 4 and 5, one can find a distinction between peritectic and eutectic features of these ternary systems. It is visible that these features degenerate at the transition of the fluoride solution, AF–(ThF4)1-x(UF4)x, from zero point, AF–ThF4 (x=0), to the unity, AF–UF4 (x=1). Besides, replacing the component, LiF, by NaF in this solution complicates a relief of the liquidus surface, expressed by а wide variety of crossings between peritectic and eutectic lines that is illustrated by phase diagrams of binary systems, LiF–ThF4 and NaF– ThF4, shown in Figure 6 [14-18]. One can see that the liquidus breaks of these systems can be described by homology series of excess phases [3]: | |
|
Figure 6: The phase diagrams of double systems: (A) LiF–ThF4 [14]; (B) NaF–ThF4 [18]. |
 (10) |
|
 (11) |
|
| Where, n=0, 1, 2, 3, 4. | |
| Sodium as a chemical element is more electropositive than lithium (Table 2), easily gives up the valent electron to fluorine, and exists in the molten fluoride rather as a cation than a covalent-bonding particle (Na═F). Obviously, it does not coordinate spatially with the covalent bond, Th═F, of the other mixture component, ThF4, and therefore essentially confines a number of allowed complex solid compounds in the fluoride system, NaF−ThF4. It is clear that the number of allowed excess phases in a binary fluoride of alkali metal, A, is decreased when the covalent bond, A═F, in the molten alloy is strengthened. | |
| One can see this in the series (10) and (11) of excess phases in two systems: LiF–ThF4 and NaF–ThF4, having different coefficients (3 and 2) at n in the multiplier, mA.ThF4. | |
| From this point of view, the complex morphology of liquidus plot [19] for KF−ThF4 system in Figure 7 can be explained by very small portion of the covalent bond, K═F, in the potassium fluoride as a more electropositive chemical element than sodium (Table 2). Therefore, we can obtain the following homology series for excess phases [3]. | |
|
Figure 7: The phase diagram of KF–ThF4 system [19]. |
 of the system, KF–ThF4. |
|
| One can see that the series (12) has the coefficient, 1, at n in the multiplier, mK.ThF4, i.e. the number of ThF4 molecules in the chemical formula of the allowed excess phases changes by 1 in contrast to system, NaF–ThF4, (by 2) and the more so for LiF–ThF4 (by 3) [3]. | |
| Thus, the more portion of covalent bond, A═F, in alkali fluorides (AF) of double systems, AF−ThF4, ordered by the growth of alkali-metal electro negativity (Table 2): The more simple the phase diagram of AF– ThF4. | |
| K═F < Na═F < Li═F, (13) | |
| It concerns also actinide fluorides, AF–AnF4. So, in replacing ThF4 in the LiF–ThF4 system by uranium fluoride of the more electronegative metal than thorium (Table 2), we obtain the phase diagram of LiF–UF4 in Figure 8 simpler [14] than the one for LiF–ThF4 system (Figure 6A). | |
|
Figure 8: The phase diagram of LiF–UF4 system [14]. |
| The simple morphology of LiF–UF4 liquidus is expressed by reducing the homology series of excess phases [3]. | |
 (14) |
|
| It is caused by increasing the coefficient at n up to 5 in the multiplier, mU.LiF, in comparison with 2 as a common coefficient at n in the homology series of excess phases [3] for all alkali fluorides, AF, in (10) – (12). | |
 (15) |
|
| It is significant that the liquidus surface of KF–NaF–LiF system in its composition triangle has only eutectic features (Figure 3). Obviously, it is caused by absence of alkali-fluoride compounds, i.e. the homology series of excess phases degenerates. It is due to the great size difference (more than 30%) of alkali cations (Table 2). Therefore in forecasting phase diagrams of any fluoride mixture, it is necessary to take into account the electronic properties of the initial components. | |
| For example, the binary systems, BeF2–ThF4 and BeF2–UF4, with the essentially different electronic properties of metal components (Table 2) have degenerated homology series of excess phases: only the initial components, BeF2 and AcF4, precipitate from the molten salts (Figure 9). The eutectics are strongly shifted to BeF2 side of phase diagrams (2%mol of AcF4) due to a significant difference of melting points of these fluorides [14,19,20]. | |
|
Figure 9: The phase diagrams of binary systems (A) BeF2–ThF4 [14]; (B) BeF2–UF4 [20]. |
| On the contrary, the binary system, LiF–BeF2, has the single complex compound, 2LiF–BeF2, (Figure 10A) [21]. It reduces to the peritectic point at ∼34%mol of BeF2 and provides almost equimolecular composition of the eutectics (48% mol of BeF2) in contrast to the systems, BeF2–ThF4 and BeF2–UF4 that have no complex compounds. | |
|
Figure 10: The phase diagrams of binary systems: (A) LiF–BeF2 [21]; (B) NaF–BeF2 [14]. |
| Lithium and actinide fluorides have such the different phase diagrams in the mixture with BeF2 due to lithium is more electropositive than uranium and thorium (Table 2). From this point of view, the phase diagram of NaF–BeF(2) [14] (Figure 10B) is caused by sodium as more electropositive element than lithium (Table 2). | |
| Thus, the molten fluorides are lined up in strengthening the covalent bond, M═F, according to the growth of electro negativity, Ξ, of their metals [22]: | |
 (16) |
|
| Where, ⇒ specifies the increase of covalent bond, M═F, in the fluoride, MFm. | |
| The covalent bonds break spherical symmetry of the pair potential of ions and lead to molecular clustering the salt melts [23]. It influences on their thermodynamic properties in whole and, particularly, on eutectic points in the system compositions. One can see this in comparing the eutectic points of binary systems, LiF–MFm, where M designates Th, U, Zr, and Be [3]: | |
 (17) |
|
| It is obvious that the molar portion of LiF in the excess phases at the left and the right of the eutectics (denoted by ║) is decreased from unity (at the left) up to zero (at the right). | |
Discussion of Results |
|
| The valent electrons in molten compounds responsible for ionic and covalent bonds influence on the liquidus morphology of any salt. So, the predominant cause of covalent bond, Be═F, in BeF2 [24] defines the characteristic feature of the liquidus surface of LiF− ThF4BeF2 and LiF−UF4−BeF2, expressed by a narrow (≤ 2% mol of the heavy component) low-temperature “terrace” along the binary side, LiF−BeF2, in the composition triangles of these systems [14]. It is easy to remove this defect in replacing AcF4 by the low-melting zirconium fluoride (Table 1) having the atomic radius per ~20% less than the one of actinides (Table 2). The eutectic region of LiF–ZrF4–BeF2 extends up to the vertex, ZrF4, achieving 20% mol of MeF4 in the binary system, ZrF4–BeF2 [21]. | |
| At the same time, the influence of the metal electro-negativity on the liquidus morphology becomes significant when the relations, ΔTm/ Tm and ΔΞ/Ξ, are comparable. So, uranium as more electronegative element than thorium (ΔΞ/Ξ ∼ 3%) has the narrower low-temperature “terrace” on the slope of LiF–UF4–BeF2 liquidus, in spite of the fact that Tm of UF4 on ~6% is lower than the one of ThF4 [14]. | |
| Therefore, forced changing Fermi level, εF, (as RedOx potential) in the band-gap, εg, to the hypo-stoichiometric (reduced) molten fluoride (Figure 2B) can become a very effective technique for selective precipitating given components from the melt and dissolving solid phases in it | |
The reduction level of the molten salt, for example FLiNaK, is
confined by precipitating the first of basic metals: Li, Na, K. One can
expect that it is potassium according to (16). Indeed, its covalent-bond portion is less 13% opposite to sodium (≤26%) and lithium (≤40%).
Then for FLiNaK, Mi c+ in (8) can be evaluated as 0.28, 0.09, and 0.36
for Li, Na, and K respectively. For conservative magnitude of  in
(9) equal to approximately 10–6 for Li, Na, and K [10], Fermi level
will reach the reduction limit at 1000 K when just potassium begins
to precipitate from liquid FLiNaK at  in contrast to
sodium which begins to precipitate at RedOx potential on 120 mV
lower, i.e. electrochemical maintaining the given quality of molten salt
is very sensitive to changing Fermi level in its band gap. |
|
| For providing such the maintaining, one can use a solid membrane having a unipolar conductivity of potassium cations in the electrochemical cell of the kind [25]. | |
 (18) |
|
Where, a liquid-metal measuring electrode, Pb [K], as a layer
in a felt of thickness less than 0.1 mm. This cell can realize a fine
coulomb-metric titration of potassium atoms through 
membrane for reducing FLiNaK up to the given quality (Figure 2B). |
|
Conclusions |
|
| The precise method of coulomb-metric titration is offered for providing the given properties of molten-salt compositions by forced changing Fermi level (RedOx potential) in the band gap of nonstoichiometric molten salts. | |
| It is shown that the electrons in molten salts, being responsible for ionic and covalent bonds, strongly influence on the liquidus morphology of these systems. Therefore managing the electrochemical potential (Fermi level) in the band gap of the non-stoichiometric molten fluorides can be the very effective technique for selective precipitating given components from the melt and dissolving solid phases in it at forced changing Fermi level of the molten salts. | |
| From these results, it is possible to classify impurity solutions, to estimate the degree component dissociation as a function of Fermi level of non-stoichiometric salts. | |
| The maintenance with high accuracy on the given level of the RedOx potential of MSR fuel composition at continuous and precise monitoring this parameter in the first loop is the key factor of a molten-salt technology. | |
Acknowledgments |
|
| Authors are pleased to acknowledge Dr. E.I. Grishanin for joint developing the electrochemical RedOx gauge [25] and discussing this work. | |
References |
|
|
|
