Research Article, Res Rep Math Vol: 1 Issue: 1

On Statistically (I) - Sequential Spaces

Renukadeviz V^* and Prakash B

Center for Research and Post Graduate Department of Mathematics, Ayya Nadar Janaki Ammal College, Inida

*Corresponding Author : Renukadevi V
Center for Research and Post Graduate Department of Mathematics, Ayya Nadar Janaki Ammal College(Autonomous), Sivakasi 626124, Tamil Nadu, India
Tel: 04562-254100
E-mail: renu_siva2003@yahoo.com

Received: July 21, 2017 Accepted: August 21, 2017 Published: August 28, 2017

Citation: Renukadeviz V, Prakash B (2017) On Statistically (I) - sequential spaces. Res Rep Math 1:1.

Abstract

Keywords: Phrases statistical convergence; I-convergent sequence; Sequential space

Introduction

The concept of convergence of a sequence of real numbers has been extended to statistical convergence independently by Fast [1,2] and Schoenberg [3]. If 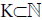then K_n will denote the set {K: k≤n} and |Kn| stands for the cardinality of K: The natural density of K is defined by

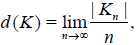
if the limit exists [4,5]. A sequence {X_n} in a topological space X is said to converge statistically [6] (or shortly s-converge) to x∈X, if for every neighborhood U of 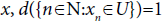, Any convergent sequence is statistically convergent but the converse is not true [7]. But in general, s-convergent sequences satisfy many of the properties of ordinary convergent sequences in metric spaces. It has been discussed and developed by many authors [8-16].

The concept of I-convergence of real sequences [17,18] is a generalization of statistical convergence which is based on the structure of the ideal I of subsets of the set of natural numbers. In the recent literature, several works on I-convergence including remarkable contributions by salat et al. have occurred [15-20]. The idea of I-Convergence has been extended from the real number space to a topological space [14] and to a normed linear space [21].

I-convergence coincides with the ordinary convergence if I is the ideal of all finite subsets of 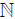and with the statistical convergence if I is the ideal of subsets of 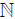of natural density zero.

Throughout this paper, (X, τ) will stand for a topological space and I for a nontrivial ideal of 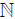, the set of all positive integers. X_n→x denotes a sequence{X_n} converging to x Let X be a space and P⊂X A sequence {X_n} converging to x in X is eventually in P if 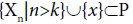for some 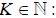it is frequently in P if 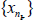is eventually in P for some subsequence 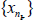of{Xn}. Let P be a family of subsets of X. Then ∪P and ∩P denote the union ∪{P|P∈P}, and the intersection ∩{P|PP}, respectively. We recall the following definition [22].

Definition 1

If X is a nonvoid set, then a family of sets is I ⊂ 2^X is an ideal if (i) A, B∈I implies A∪B∈I and (ii)A ∈I, B⊂A, implies B∈I.

The ideal is called nontrivial if I ≠ ∅ and X∉I. A nontrivial ideal I is called admissible if it contains all the singleton sets. Several examples of nontrivial admissible ideals may be seen in [17].

Definition 2

A sequence {X_n}. in X is said to be I-convergent to x₀∈X if for any nonvoid open set U containing x₀, 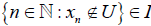We call x₀ as the I-limit of the sequence {X_n}[14] .

Definition 3

Let X be a space. P ⊂ X is called a sequential neighborhood of x in X, if each sequence convergent to x∈X is eventually in P. A subset U of X is called sequentially open if U is a sequential neighborhood of each of its points. X is called a sequential space [24] if each sequentially open subset of X is open.

Definition 4

O is I-sequentially open if and only if no sequence in X \O has an I-limit in O [1].

Definition 5

A subset A of a space X is said to be I-sequentially closed set if for every sequence {X_n}in A with {X_n}I-converges to x, then x∈A [1].

Definition 6

A topological space is I-sequential when any set O is open if and only if it is I-sequentially open.

Definition 7

A space X is called locally I-sequential space if every point of x∈X has a neighborhood which is an I-sequential space.

Even though we mainly deal with I-sequential spaces, we see the basic definition for s-sequential space since it will be useful for the examples which deal with s-sequential spaces. An I-sequential space X is statistically sequential if .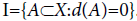

Definition 8

A space X is called statistically sequential(or shortly s-sequential) space [6] if for each non-closed subset A⊂X, there is a point x∈X \A and a sequence 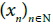in Astatistically converging to x.

There is another way to define s-sequential space.

Definition 9

A subset A of a space X is said to be a statistically sequentially open set (s-sequentially open) [25] if for any sequence {X_n} statistically converge to x and x∈A then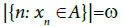

A topological space is s-sequential when any set O is open if and only if it is s-sequentially open.

Definition 10

A subset K of the set 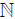is called statistically dense [6] if d(k)=1.

Definition 11

A subsequence S of the sequence L is called statistically dense in L [4] if the set of all indices of elements from S is statistically dense.

Remark 12

1. The limit of an I-convergent sequence is uniquely determined in Hausdorff spaces [14,6] .

2. If a sequence (x_n)_n∈N converges to x in the usual sense, then it statistically converges to x . But the converse is not true in general.

3. A sequence (x_n)_n∈N is statistically convergent if and only if each of its statistically dense subsequence is statistically convergent.

4. If a sequence{X_n} I-converges to x , then every subsequence 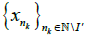is I-convergent for every I′∈I

Lemma 13

Let X be a topological space and A⊂X Then the following hold [1].

(a) A is I-sequentially open.

(b) X\A is I-sequentially closed.

I-sequential spaces 14

In this section, we answer the question 2 [25]: Is the product of two s-sequential spaces s-sequential?

By the Example 1 that product of two s-sequential spaces need not be s-sequential. Also, we give the necessary and sufficient condition for the product to be in most general case of I-sequential space. And we point out the error in proposition 2 of [1].

Proposition 1

The disjoint topological sum of any family of I-sequential spaces is I-sequential.

Proof. Let X be the disjoint sum of the family {X_i}_i∈Λ of I-sequential spaces. U∩ X_i is not I-sequentially open. Thus, there is a point X_i∈ U∩ X_i and a sequence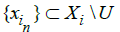 I-converges to Xi and therefore in X. Hence U is not I-sequentially open. Therefore, X is an I-sequential space.

The following Example 1 shows that the products of two s-sequential spaces need not be s-sequential.

Example 1

For each 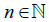let 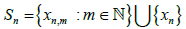be a sequence statistically converges to x such that 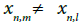if m≠l. Take 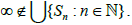Let X′ be the disjoint topological sum of Sn where 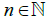and X be the space obtained from X′ by identifying x_n to ∞. Now let f: X′ → X be a natural mapping. Since each Sn is a s-sequential space and hence X′ by Proposition 1. By Theorem 1 in [25], X is a s-sequential space.

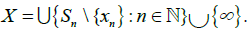
The open set in X is as follows :

1. Each point x_n,m is isolated;

2. Each open neighborhood of the point ∞ is a set V of the form

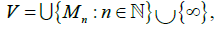
where each M_n is a dense subsequence of Sn. Next we define Y: Let

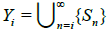Now yet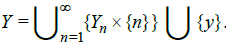

Topologize Y as follows:

Let each point of 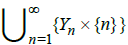be open and 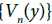be a countably local base at y, where 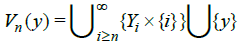. Then Y is a metric space.

Now let 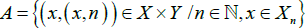. Then 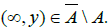Thus, A is not closed in X, Y, but statistically sequentially closed in X x Y since A has no non trivial s-convergent sequence. Suppose A has a s-convergent sequence 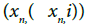statistically converges to (,y), Then 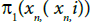statistically converges to ∞ which implies for some m, 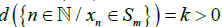. But the corresponding sequence in 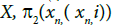statistically converges to y which is a contradiction to 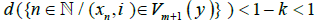. Therefore, X Y is not a s-sequential space.

Next we see the necessary and sufficient condition for the product of I-sequential spaces to be I-sequential.

Proposition 2

Every I-sequential space is a quotient of a topological sum of I-convergent sequences.

Proof. Let X be an I-sequential space. For each x∈X and for each sequence {S_n} in XI-converging to x, let I(S,x)={s_n/n=1,2,3,…}{x} be a topological space, where each sn is a discrete point and neighborhood U of x is such that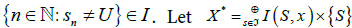 where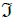 be the set of all I-convergent sequences. Now we consider a mapping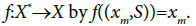

1. f is onto.

For each point x∈X there is a constant sequence S in X such that I(S,x)={s_n/n=1,2,3,…}∪{x} that is, there exists I(S,x)X{s}⊂ X* and f((x,S))=x Therefore, f is onto.

2. f is continuous.

Let U be an open set in X and (x′,S)∈f-1(U). Then there is a sequence S in X such that x′∈I(S,x) )={s_n/n=1,2,3,…}∪{x} that is, (x′,S)∈ I(S,x)x{s}⊂ X* and f((x′,S))= x′. If (x′,S). is an isolated point, then there is nothing to prove. If (x′,S)=( x,S),then there exists I′∈I such that S_n∈U for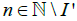 and hence 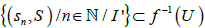which is open in I (S, X) and hence open in X*. Therefore, f^-1(U) is open in X*. Therefore, f is continuous.

3. f is quotient.

Suppose U ⊂ X and f^-1(U) is open in X*. If x₀∈U and {S_n} is I-convergent to x₀ in X, then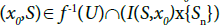 which is an open neighborhood of 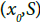in 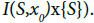Then as a subset of 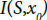x{S}, there exists I′∈I such that 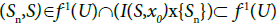for 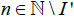and so 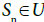for 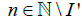. Hence U is I-sequentially open and thus open. Therefore, f is a quotient mapping.

Here I(S_n,x) is not second countable, when the set of all finite subsets of 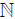is a proper subset to I and not a Hausdorff space, when the set of all finite subsets of 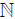properly contains I. Hence for such I, I(S_n,x) is not a metrizable space and hence its topological sum.

In Proposition 2 in [1], 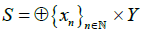is mentioned as a metric space. But it is true only when I is the set of all finite subset of .

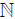Also, the following Proposition 3 is not true in general.

Proposition 3

Every I-sequential space X is a quotient of some metric space.

Suppose Proposition 3 is true. Then by Proposition 2 [1], X is an I-sequential space if it is a quotient image of a metric space. And hence I-sequential space and sequential space coincide, by Corollary 1.14 in [23] which is a contradiction to Example 2 in [25].

Lemma 2.5

Let X be an I-sequential space. If f: X→Y preserves I-convergence sequence, then f is continuous.

Proof. Let U be an open subset in Y. Since X is an I-sequential space, it is enough if we prove that f^-1(U) is an I-sequentially open subset of X.

Let {X_n}be a sequence in X which I-converges to x∈f^-1(U) By our assumption, {f(x_n)}I-converges to f(x)∈U Since U is open in Y, for some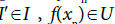 for 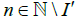. This implies 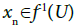for 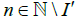. and hence f^-1(U) is an I-sequentially open subset of X. Therefore, f is continuous.

Theorem 1

Let X* and Y* be the spaces obtained from X, Y as in Proposition 2. Then the following hold

1. X* is an I-sequential space

2. (XxY)* is homeomorphic to X*xY*

3. X*xY* is an I-sequential space.

Proof 1

Let U be an I-sequential open subset of X* and (x′,S)∈U where S is an I-convergent sequence {x_n}in X with its limit x and x∈S This implies (x_n, S) I-converges to (x, S) in X*. If (x′,S)= (x_n,S) for some n, then there is nothing to prove. If 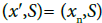then 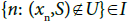since U is an I-sequentially open subset of X*. This implies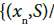 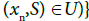is open in X* which is contained in U. Therefore, U is open in X*. Therefore, X* is an I-sequential space.

Proof 2

Let 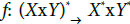be defined by 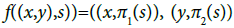where S is an I-convergent sequence with its limit in XxY and (x,y)∈S. Since projection mappingsπ₁,π₂ are continuous and by Proposition 1 in [1], π₁(s) and π₂(s) are I-convergent sequences in X and Y. respectively. Therefore, f is well defined.

(a) f is one-one and onto

Since product of I-convergent sequence is again I-convergent sequence, f is onto. Also, we easily check that f is one-one.

(b) f is continuous

Clearly, f preserve I-convergence and by Theorem, f is continuous.

(c) f ^-1 is continuous

Let U be an open set in (XxY)* and 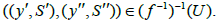If y′ and y′′ are the limit point of S′ and S′′, respectively, then S′× S′′ I-converges to ( y′, y′′). This implies that there exists i∈I such that 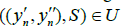for all 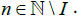Now let 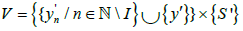is open in X* and 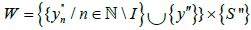is open in Y*. This implies 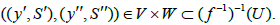For 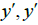are not a limit point, we can easily find an open set in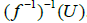. Therefore 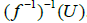is open in X*xY*.

Therefore, (XxY)*is homeomorphic to X*xY*.

3. By (a), (XxY)*is an I-sequential space. By(b) and Proposition 2.1 in [1], X*xY* is an I-sequential space.

By Lemma 3 and Definition 6, we have the following Theorem 2.

Theorem 2

Let X be a topological space. Then the following are equivalent:

(a) X is an I-sequential space.

(b) Every I-sequentially open subset of X is open.

(c) Every I-sequentially closed subset of X is closed.

Theorem 3

Each I-sequentially open (closed) subspace of an I-sequential space is I-sequential.

Proof. Let X be an I-sequential space. Suppose that Y is an I-sequentially open subset of X. By Theorem 2, Y is open in X. Let U be an arbitrary I-sequentially open subset in Y and let {xn} be a sequence in X I-converges to x∈U Then x∈Y and since Y is an I-sequentially open subset of X. there exists I′∈I such that

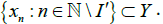Then by Remark 1.12, 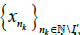is an I-convergent subsequence in Y. Since U is an I-sequentially open subset in Y , there exists I′′∈I such that 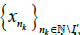is in U . That is, 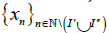is in U. Therefore, U is I-sequentially open in X . and hence open in X . This implies U . is open in Y, since Y is open in X . Therefore, Y is an I-sequential space.

If Y is an I-sequentially closed subset of X , then by Theorem 2, Y is closed in X . Let F be an I-sequentially closed subset in Y and let {x_n} be a sequence in F I-convergent to x Since Y is closed, x∈Y and hence x∈F. Therefore, F is an I-sequentially closed set in X and hence it is closed in X . Since Y is closed in X, F is closed in Y.

Proposition 4

Every locally I-sequential space X is I-sequential.

Proof. Let U be an I-sequentially open set in X . Since X is a locally I-sequential space, there exists an I-sequential neighborhood V of x With out loss of generality, assume that V is open and an I-sequential space. Since U is I-sequentially open, U ∩V is an I-sequentially open subset of V . Since U is an I-sequential space, x∈U∩V is open in V and hence in X which is contained in U. Therefore, U is open and hence X is an I-sequential space.

In the rest of the section, the space X* and the mapping φ= f: X* X are as in Proposition 2.3.

Theorem 4

The product of two I-sequential spaces X and Y is I-sequential iff φ_X xφ_Y is a quotient mapping.

Proof. Suppose φ_X xφ_Y is a quotient mapping. By (c) in Theorem 1 , X*xY*is I-sequential. By Proposition 2 in [1] and by assumption, XxY is I-sequential.

Conversely, suppose that XxY is I-sequential. Then 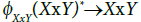is a quotient mapping (in proof of Proposition 3 ) and f-1: X*xY*→(XxY)*is also a quotient mapping (defined in proof of Theorem 1 (b) ). Since composition of two quotient mapping is again quotient, 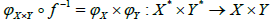is a quotient mapping.

Since a s-sequential space is not closed under Cartesian product like a sequential space, naturally, one can arise a question that “ Is subspace of a s-sequential space, s-sequential?”. The answer is not as shown by the following Example 2.

Example 2

Let S_n be the s-convergent sequence with its limit an for eachn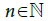that is 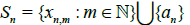and 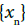be a s-convergent sequence with its limit x. Let X be the topological sum of the sequence S_n, n= 1,2,3,… and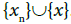. Since each S_n, n= 1,2,3,… and 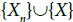is s-sequential, X is s-sequential, by Proposition 1.

Now let Y be a space obtained from X by identifying a_n to x_n.

Let f: X→Y be the natural mapping. By Theorem 4 in [25], Y is a s-sequential space but not a s-Frechet Urysohn space.

Let W be a weak base consists of the following three types of collection of weak neighbourhood of x′

If x′≠x then

If x′=x, U∈T_x then implies that

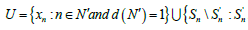is a non − thin subsequence S when .

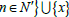Then W is a weak base of Y. But for all 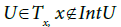erefore, Y is not a s-Frechet Urysohn space by Theorem 4 in [25]. Now let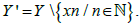

Then {x}is s-sequentially open in Y′. Suppose{x}is not a s-sequentially open. Then there is a sequence 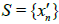in Y′ s-converges to x. Then we get a contradiction to Y is not a s-Frechet Urysohn space.

Let A be a subset of Y with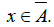

If x_n∈A, for all n∈N′ where N′ is a non-thin subsequence of{X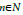_n} then 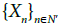s-converges to x, by Remark 1.2 (3) in [25].

If x_n∈A, for all n∈N′ where N′ is a thin subsequence of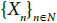 Then A∩S_n is a non-thin subsequence of Sn for all n∈N′′ where N′′ is a non-thin subsequence of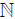

Suppose A∩S is a non-thin subsequence of S, then A∩S itself is a s-convergent sequence.

Suppose A∩S is a thin subsequence of S, then S\A is again s-convergent to x. Now we form a one-to-one function f between 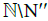and N′′ by nth element in 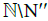goes to n^th element in N′ Do the same between S\A and 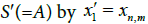goes to 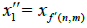that is, m^th element of 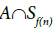Then 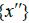is a sequence in A s-converges to x. Suppose not 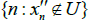is a non-thin subsequence of 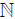. Now we form an open set U′ from U as follows:

If 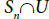is non-dense in S_n where 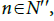then eliminate the elements of S_n from U to get U′ .

If 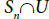is dense in S_n where 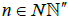and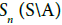 is a non-thin subsequence of S_n , then eliminate the element x_n,m from U to get U′ where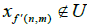. Then 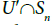is dense in Sn, since both 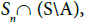and 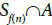are non-thin subsequences of S_n and S_f(n) respectively.

Now 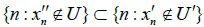which is a non-thin subsequence of 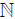. Therefore, S\A is not a s-convergent sequence which is a contradiction.

Therefore, 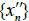is a sequence in A s-convergent to x and hence Y is s-Frechet Urysohn space which is a contradiction. Therefore, {x} is s-sequentially open in Y′ but not open in Y′. Therefore, Y′ is not s-sequential.

Next we see the necessary and sufficient condition for which a subspace of an most general case I-sequential space is I-sequential.

Theorem 5

A subspace Y of an I-sequential space X is I-sequential iff 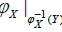is a quotient.

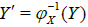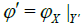Proof. Let and and let 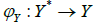be a mapping as in the proof of Proposition 3. Suppose φ′ is a quotient mapping and let 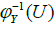be open in Y*where U⊂Y.

Since φ′ is quotient, it is enough if we prove that 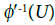is open in Y′.

Let 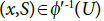where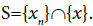 Suppose 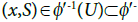¹(U), then there is nothing to prove.

Suppose 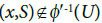and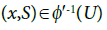

Let 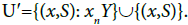Since I(S,x), is open in X* and 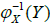is a subspace of 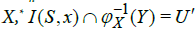is open in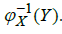

Now let

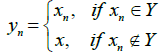
Then {Y_n}in Y I-converges to x∈U which implies (Y_n,S′) I-converges to 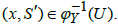That is

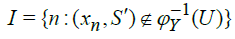
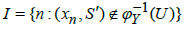
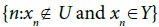
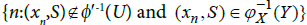
Now let 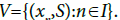Then 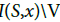is open in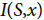. Therefore, 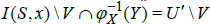is open in 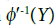and 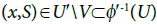Therfore 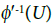is open in Y′ and hence U is open in Y. Therefore, φ_y is a quotient mapping. By Theorem 2 and Proposition 1 in [1], Y is an I-sequential space.

Conversely, let Y be an I-sequential space. By Proposition 3, φ_y is a quotient mapping. Now let 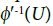is open in Y′ where U⊂Y Since 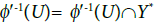is open in Y*, U is open in Y. Therefore, φ′ is a quotient mapping [26,27].

Finally, we give some easy propositions whose proofs are omitted.

Proposition 5

The continuous open or closed image of a I-sequential space is I-sequential.

Proposition 6

If the product space is I-sequential, so is each of its factors.

References

1. Pal SK (2014) I-sequential topological spaces, Appl Math E-Notes 14: 236-241.
2. Fast H (1951) Sur la convergence Statistique. Colloq Math 2: 241-244.
3. Schoenberg J (1959) The Integrability of certain function and related summability methods. Amer Math Monthly 66: 361-375.
4. Halberste H, Roth KF (1993) Sequences. Springer, New York, USA.
5. Niven I and Zuckerman HS (1980) An introduction to the theory of numbers. Math Slovaca 30: 139-150.
6. Maio GD, Kocinac LDR (2008) Statistical convergence in topology. Topology Appl 156: 28-45.
7. Salat T (1980) On statistically convergent sequences of real numbers. Math Slovaca 30: 139-150.
8. Connor J, Kline J (1996) On statistical limit points and the consistency of statistical convergence. J Math Anal Appl 197: 392-399.
9. Erdos P, Tenenbaum G (1989) Sur les densities de certaines suites dentiers. Proc London Math. Soc 59: 417-438.
10. Fridy JA (1985) On statistical convergence. Analysis 5: 301-313.
11. Fridy JA (1993) Statistical limit points. Proc Amer Math Soc 118: 1187-1192.
12. Fridy JA, Miller HI (1991) A matrix characterization of statistical convergence. Analysis 11: 59-66.
13. Miller HI (1995) A measure theoretical subsequence characterization of statistical convergence. Trans Amer Math Soc 347: 1811-1819.
14. Lahiri BK, Das P (2005) I and I*-convergence in topological spaces. Math Bohem 130: 153-160.
15. Lahiri BK, Das P (2003) Further results on I-limit superior and I-limit inferior. Math Commun 8: 151-156.
16. Macaj M, Salat T (2001) Statistical convergence of subsequences of a given sequence. Math Bohem 126: 191-208.
17. Kostyrko P, Salat T, Wilczy W (2000) n Ski, I-convergence. Real Analysis Exch 26: 669-685.
18. Kostyrko P, Macaj M, Salat T, Sleziak M (2005) I-convergence and a extremal I-limit points. Math Slovaca 55: 443-464.
19. Baláz V, Cervenansky J, Kostyrko P, Salat T (2002) I-convergence and I-continuity of real functions. Acta Math 5: 43-50.
20. Demirci K (2001) I-limit superior and limit inferior. Math Commun 6: 165-172.
21. Salat T, Tripathy BC, Ziman M (2005) On I-convergence field. Italian J Pure Appl Math 17: 45-54.
22. Kuratowski C (1958) Topologie. PWN Warszawa.
23. Franklin SP (1965) Spaces in which sequences suffice. Fund Math 57: 107-115.
24. Pehlivan S, Guncan A, Mamedov MA (2004) Statistical cluster points of sequences in finite dimensional spaces. Czechoslovak J Math 54: 95-102.
25. Zhongbao T, Fucai F (2015) Statistical versions of sequential and Frechet Urysohn spaces. Adv Math 44: 1-10.
26. Miller HI, Orhan C (2001) On almost convergent and statistically convergent subsequences. Acta Math Hungar 93: 135-151.
27. Pehlivan S, Mamedov MA (2000) Statistical cluster points and Turnpike. Optimization 48: 93-106.