Research Article, J Nucl Ene Sci Power Generat Technol Vol: 12 Issue: 3
Radiation of a Point Magnetic Dipole Moving in a Medium with Superluminal Speed
Seil S. Sautbekov* and Kuralay N. Baisalova
1Department of Plasma Physics and Nanotechnology, Al-Farabi Kazakh National University, Almaty 050040, Republic of Kazakhstan
*Corresponding Author: Seil S. Sautbekov,
Department of Plasma Physics and
Nanotechnology, Al-Farabi Kazakh National University, Almaty 050040, Republic
of Kazakhstan
E-mail: curalay@mail.ru
Received date: 22 May, 2023, Manuscript No. JNPGT-23-99425;
Editor assigned date: 24 May, 2023, PreQC No. JNPGT-23-99425 (PQ);
Reviewed date: 09 June, 2023, QC No. JNPGT-23-99425;
Revised date: 16 June, 2023, Manuscript No. JNPGT-23-99425 (R);
Published date: 23 June, 2023 DOI: 10.4172/2325-9809.1000334.
Citation: Sautbekov SS, Baisalova KN (2023) Radiation of a Point Magnetic Dipole Moving in a Medium with Superluminal Speed. J Nucl Ene Sci Power Generat Technol 12:3.
Abstract
Simple asymptotic expressions have been obtained for the spectral density of the field and energy losses of Cherenkov radiation from a magnetic dipole with a constant magnetic moment moving uniformly in a medium with superluminal speed. The spectral density is calculated by Fourier transforming in time an arbitrarily moving magnetic dipole previously obtained in a more general form from the relativistic vector magnetic potential. The Fourier inversion integration was performed using the asymptotic saddle-point method. The conditions and angular size of the Vavilov-Cherenkov cone of radiation are derived. It is shown that the radiation waves propagate at a sharp angle to the direction of the dipole's motion, and the spectral density of the radiation field is directly proportional to its frequency raised to the power of three halves. The results are compared with previously known ones. It is found that the expression for energy losses per unit length of the dipole's path is identical to Frank's result when the dipole moment is parallel to the velocity of motion.
Keywords
Analogy method; Electricity and magnetism; Potential; Electric field; Magnetic field; Dipole
Introduction
It is known that Tamm and Frank Nobel Prize laureates, proposed the mechanism of Vavilov-Cherenkov radiation for charged particles and a quantitative theory based on classical electrodynamics equations. Later, Ginzburg and Fermi generalized and gave a quantum description of the Cherenkov ect. However, it is worth giving the final historical tribute to the English physicist and mathematician Oliver Heaviside and the German physicist and mathematician Arnold Sommerfeld for predicting the radiation from a uniformly moving charge at super-light speeds, which Heaviside had already made by Sommerfeld [1-7]. However, the emergence of the theory of relativity in 1905 led to the conclusion that a charge cannot move at a speed greater than the speed of light. Therefore, their work was forgotten for many years, and no one thought to consider the motion of a charge not in a vacuum, but in a medium.
The above-mentioned classical theory for charged particles is quite accurately consistent with experiments, so it can be considered that the quantum theory is only useful from a methodological point of view.
The Cherenkov ect has found wide application in physics, for example, Cherenkov counters allow for the detection of particles with high velocities and the differentiation of two particles arriving almost simultaneously, determining their mass and energy. Such a detector was used in the discovery of antiprotons, antineutrons, and other elementary particles [8-13].
The problem of radiation by a superluminal particle in a medium with an electric dipole moment was considered by Frank [14]. The theory of Cherenkov radiation for linear electric and magnetic multipoles was developed in the well-known works of Frank, Ginzburg and other authors [15-18]. In this case, magnetic multi-poles were considered as a combination of magnetic charges, and the wave field was considered as a result of interference of waves emitted by the charges that make up the field. In other words, all the aforementioned approaches are essentially based on the principle of superposition using the Lienard-Wiechert charged particle potential technique.
However, for a magnetic dipole oriented perpendicular to the direction of its motion, when the velocity of the dipole is equal to the phase velocity of light in the medium, the radiation energy is not zero, which does not correspond to the truth or the formula is inapplicable in this case. The question of this anomaly, found as early as 1942, has been discussed repeatedly and remains open to this day.
Our method, based on the vector potential of the dipole, is free from techniques such as using magnetic charges and wave interference, as well as taking into account the polarization of the medium as the dipole passes through it. This paper considers the radiation of a magnetic dipole with a constant dipole moment, uniformly moving in a medium with superluminal velocity. Essentially, this paper is a continuation of the application of previously obtained results in solving a new problem Cherenkov-Vavilo radiation [19].
An expression for the spectral representation of the field of a point dipole will be obtained by Fourier transforming the general solution which will easily allow us to consider the losses of Cherenkov-Vavilov radiation energy.
Materials and Methods
Spectral representation of the Cherenkov radiation field
The field of radiation from a magnetic dipole in the ultra-relativistic case can be represented as:
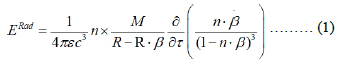
Where the magnetic dipole moment M is assumed to be constant. It should be noted that n=R/R is the unit vector directed towards the observation point r from the location of the dipole (with the radius vector r(τ)), R(τ)=|r-r(τ)|where τ is the moment in time that determines the location of the dipole, which is the root of the equation t-τ=R(τ)/c, t is the moment in time at the observation point r, t-τ is the time delay, and c is the speed of light in the medium. The spectral representation of the Vavilov-Cherenkov radiation eld can be obtained by calculating the Fourier transform of the expression:
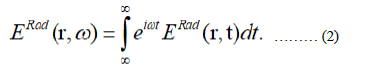
We will only switch to the limit constant value of the dipole speed (u=βc) in the final expressions of (2). Using the expressions
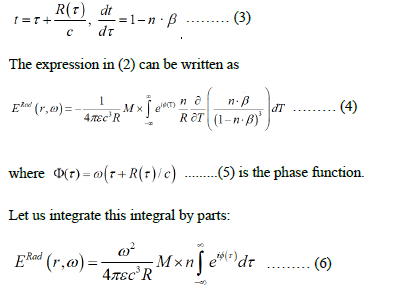
In the far zone r » r(τ), taking the factor n/R outside the integral, since it is valid phase function [19].
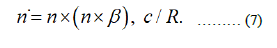
Integrating by parts again and taking into account the expression for the derivative of R(τ) [19].
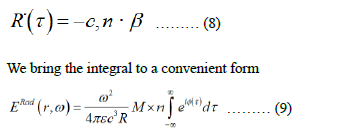
It is expedient to evaluate the integral using the saddle point method, for which we expand the phase function in a Taylor series:
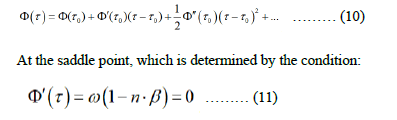
Which can be represented as: τ0=r(τ0)/u,
For convenience, we align the coordinate system with the location of the dipole at the initial moment.
Note that expression (11) coincides with the condition for Vavilov- Cherenkov radiation, which determines the angular size of the radiation cone:

The integration path in equation (9) passes from left to right [-∞-i0, τ0-i0], [τ0+i0, ∞+i0] shifted parallel to the real axis by small negative and positive imaginary quantities respectively before and after the saddle point τ0. The contour at the saddle point intersects the real axis at an angle of π/4. Note that it is useful to have in mind the integral
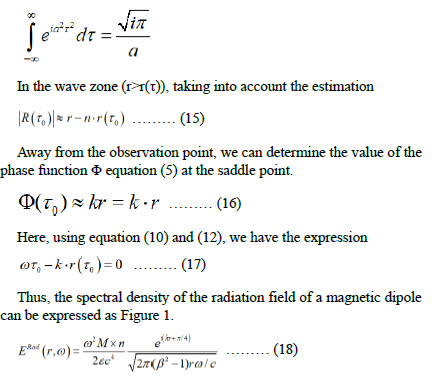
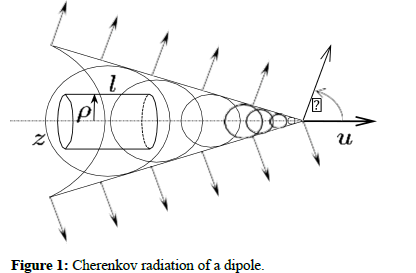
Thus, the spectral density of the radiation field of a magnetic dipole can be expressed as Figure 1.
The condition for applying the saddle point method, Φ″(τ0)»1, is equivalent to the condition β>1, which is consistent with equation (12).
It should also be noted that due to the scalar product in equation (16), the wave vector is parallel to the radius vector and, according to equation (11), makes an angle θ with the velocity vector. From this, we can conclude that the wave front of the radiation is conical. Indeed, we obtain the equation for the generating cone
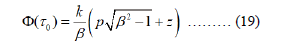
by rewriting the phase Φ(τ0) in equation (14) with (12) in cylindrical coordinates.
Energy losses of a point dipole due to Cherenkov radiation
To calculate the energy losses of a point magnetic dipole due to Cherenkov radiation, we surround the trajectory of the dipole with a cylindrical surface of radius ρ and length l, with its axis aligned with the z-axis.
The energy loss per unit time is determined by the flux of the Poynting vector S through this surface.
Therefore, the expression for energy losses can be easily obtained as

Let us consider a simpler special case when the magnetic moment is oriented (M ⇈ u) in the direction of motion (along the z-axis). Therefore, it makes an angle θ with the direction of wave propagation, i.e.|M × n|=Msinθ.
Due to the axial symmetry of the fields, the integrand does not depend on the angle ᵩ, i.e. the radiation is the same along all the generatrices of the cone. Therefore, the integral in equation (20) over ϕ is equal to 2π.
Taking into account the above and noting that ρ=rsinθ we substitute the expression for the electric field equation (18) into (20):
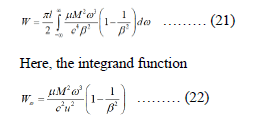
Determines the energy radiated per unit path length and frequency ω. It is important to note that the obtained expression for the losses due to Vavilov-Cherenkov radiation, Wω, turned out to be identical to the result of Frank's work, obtained and verified by different methods [15]. Indeed, to verify the validity, it is sufficient to make the following substitutions in equation (22): c → c/n, β → nβ (n is the refractive index of the medium), since the notation of the speed of light is used in the medium, not in a vacuum.
Results and Discussion
A simpler and easier way to determine the spectral density of dipole radiation from the Vavilov-Cherenkov effect equation (18) in our opinion is the Fourier transformation in time of the expression for the electric eld of a dipole moving arbitrarily with a variable magnetic moment, obtained in the works of Geras and Sautbekov using different methods [19,20]. As a result, it becomes possible to determine the energy loss per unit length Wω.
In the special case when the dipole moment is parallel to the velocity and, as a rule, the radiation fields have axial symmetry, we have the same formula for Wω obtained earlier by Frank [15].
It should be noted that in reality, the case of a magnetic dipole turns out to be much more complex when the moment is oriented perpendicular to the velocity, since Vavilov-Cherenkov radiation along the cone generators is anisotropic. Perhaps for this reason, the results of the works and obtained by different methods, differ [21].
In order to choose a solution with reliable accuracy among them, in future works we plan to apply the vector potential technique [19]. In the proposed method, asymptotic integration by the saddle-point method can be replaced by an exact integral, thanks to the vector potential of the dipole for Vavilov-Cherenkov radiation.
Along with this, a resonant problem arises related to the electric dipole, as a moving particle with a magnetic moment additionally induces an electric moment and contributes to the overall solution. The final results should satisfy, in our view, the principle of duality, due to the symmetry of Maxwell's equations [22].
It should be noted that the dipole moment of the particle, unlike in the above-mentioned works, is considered by us as a vector physical quantity. This allows us to avoid additional assumptions and routine procedures, such as considering the dipole as a system of individual charges or interference of waves emitted by individual charges of the dipole, as is the case in standard approaches.
Conclusion
Simple asymptotic approximation of the spectral density of the Vavilov-Cherenkov radiation electric field equation (18) and an expression for energy losses equation (20) have been obtained.
It has been shown that Vavilov-Cherenkov radiation waves, represented as an asymptotic expansion of a cylindrical Bessel function, propagate at a sharp angle θ that determines the angular size of the radiation cone equation (12) with respect to the direction of the dipole's motion, and the spectral density of radiation is directly proportional to its frequency raised to the power of 8 three halves.
The identity of the expression for energy losses per unit path length Wω in equation (22) with the result obtained by Frank has been compared and discovered when the dipole moment is parallel to the velocity of motion. The obtained expressions may be useful in further studies of the spectral analysis of magnetic dipole radiation, especially with an induced electric moment.
References
- Tamm IE, Frank IM (1937) Coherent radiation of fast electrons in a medium. SSSR 14:107-112.
- Tamm IE, Frank I, Tamm I (1991) Coherent visible radiation of fast electrons passing through matter. Selected Papers 29-35.
- Frank IM (1971) Coherent radiation of the fast electron in medium. Joint Inst Nuc Res.
- Ginzburg VL (1940) Quantum theory of radiation of electron uniformly moving in medium. Zh Eksp Teor Fiz 10:589.
- Fermi E (1940) The ionization loss of energy in gases and in condensed materials. Phys Rev 57(6):485.
- Heaviside O (1888) The electro-magnetic effects of a moving charge. The Elect 22:147-148.
- Sommerfeld A (1904) Zur elektronentheorie. II. Grundlagen für eine allgemeine Dynamik des Elektrons. Mathematisch-Physikalische Klasse 1904:363-439.
- Frank IM (1946) Radiation of Electrons Moving in Medium with Superluminal Velocity. Usp Fiz Nauk 30:149-83.
- Jelley JV (1955) Cerenkov radiation and its applications. Br J Appl Phys 6(7):227.
- Jelley JV (1996) The feasibility of detecting neutrinos of cosmic origin by radio frequency Cherenkov radiation in Antarctic ice. Astro Phys 5(3-4):255-261.
- Frank IM (1991) Neutron optics and ultracold neutrons. Uspekhi Fizicheskikh Nauk 161(11):109-27.
- Bolotovskii BM (2009) Vavilov-Cherenkov radiation: Its discovery and application. Physics-Uspekhi 52(11):1099.
- Denisov SP (2015) Use of Cherenkov counters in experiments at accelerators for particle identification. Physics-Uspekhi 58(5):480.
- Frank IM (1984) Vavilov-Cherenkov radiation for electric and magnetic multipoles. Soviet Physics Uspekhi 27(10):772.
- Ginzburg VL (1996) Radiation by uniformly moving sources (Vavilov–Cherenkov effect, transition radiation, and other phenomena). Physics-Uspekhi 39(10):973.
- Ginzburg VL (2002) Some remarks on the radiation of charges and multipoles uniformly moving in a medium. Physics-Uspekhi 45(3):341.
- Bolotovskii BM (1957) The theory of the Vavilov-Cherenkov effect. Uspekhi Fiz. Nauk 62.
- Sautbekov S (2019) The vector potential of a point magnetic dipole. J Magn Magn 484:403-407.
- Heras J (1998) New approach to the classical radiation fields of moving dipoles. Physics Letters A 237(6):343-348.
- Balazs NL (1956) Cerenkov radiation of neutral particles with a magnetic moment. Physical Review 104(5):1220.
- Sautbekov SS, Sirenko Y, Asylbekova AG (2019) Consistency of the definition of the magnetic moment with the principle of permutational duality. Telecommun Radio Eng 78(11).
- Sautbekov SS, Baisalova KN, Sirenko YK (2021) Analogy approach in solving the problem of a moving electric dipole. AIP Advances 11(10):105012.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi