Research Article, Res Rep Math Vol: 1 Issue: 1

Stability under C1 - Perturbation of Dynamical System

Osipenko GS^* and Korzh TN

Lomonosov Moscow State University, Moscow, Russia

*Corresponding Author : Osipenko GS
Lomonosov Moscow State University, Moscow, Russia
Tel: +7 495 939-10-00
E-mail: george.osipenko@mail.ru

Received: September 01, 2017 Accepted: September 18, 2017 Published: September 25, 2017

Citation: Osipenko GS, Korzh TN (2017) Stability under C1 - Perturbation of Dynamical System. Res Rep Math 1:1.

Abstract

Keywords: Hyperbolicity; Spectrum of differential; Complementary differential; Chain-recurrent set; Projective bundle; Symbolic image

Introduction

Let f: M→M be a diffeomorphism of a compact manifold M ⊂ R^d and let ρ be a distance on M. The space of diffeomorphisms is endowed with a topology generated by the C¹-distance ρ₁ defined as follows. The C¹-distance ρ₁ between f and g is defined by

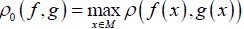
The norm of the differential Df: TM→TM (TM is the tangent bundle of M) is defined by

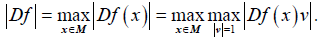
The C¹- distance ρ₁ is defined by

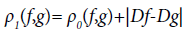
Consider a smooth discrete system

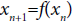(1)

generated by the diffeomorphism f.

Definition 1

For a given ε>0 an infinite in both directions sequence 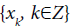is called an ε-trajectory (a pseudo-trajectory or a pseudo-orbit) of f if for any k.

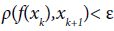
A pseudo-trajectory {x_k} is said to be p-periodic if x_k = x_k+p for each k, in this case the points x_k are named ε-periodic.

It should be noted that, in practice, an exact orbit is seldom known, and usually we find nothing more than an ε-trajectory for sufficiently small positive ε.

Definition 2

A point x is called chain recurrent if x is ε- periodic for each positive ε-, i.e., there exists a periodic ε-trajectory passing through x. A chain recurrent set is the set of all the chain recurrent points, it is denoted CR or CR(f). A set Ω ⊂ CR is called a component of a chainrecurrent set if every two points in Ω can be joined by a periodic ε-trajectory for every ε>0.

We recall that P∈M is a wandering point if there exists a neighborhood V of p and an integer Ko that fk(V)∩V=∅ for |K|>Ko Otherwise we say that p is nonwandering. We write Ω or Ω(f) for the set of nonwandering points of f. It is well known [1] that Ω(f) is compact, invariant, and contains α and ω- limit points. Hence, each trajectory starts and ends at Ω(f), i.e., the dynamics of a system is ultimately concentrated on Ω(f). It is known [2], that the chain recurrent set CR is invariant, closed, and contains periodic, homoclinic, nonwandering and other singular trajectories. Thus we have the inclusion

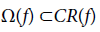
There are the examples which prove that the above inclusion is strict, i.e. Ω(f)≠ CR(f). It should be remarked that if a chain recurrent point is not periodic and dim M>1 then there exists as small as one likes perturbation of f in C^o-topology for which this point is periodic [3-5]. One may say that chain recurrent points generate periodic trajectories under a small C^o-perturbation. Note that, in our computer investigations, the chain recurrent points look like as periodic pointsa since we work with pseudo-trajectories only. It should be noted that there is a constructive method of localization of the chain recurrent set (see below), while a method for construction of the nonwandering set is unknown.

Definition 3

A diffeomorphism f is said to be CR-stable if for any ε>0 there exists δ>0 that the inequality ₁(f,g)<δ implies the existence of a homeomorphism h: CR(f)→CR(g) that hf=gh and ρ₀(h,id)<ε where id is the identity mapping.

A diffeomorphism f is said to be Ω-stable if for any ε>0there exists δ>0 that the inequality ρ₁(f,g)<δ implies the existence of a homeomorphism h: Ω(f)→ Ω(g) such that hf=gh and ρ₀(h,id)<ε where id is the identity mapping.

The structural stability was originated by Andronov et al. [6]. Summarizing the results of S. Smale et al. [7], Shub et al, [5], Palis et al. [1], Franke et al. [8], we obtain the following theorem.

Theorem 1

The following statements are equivalent:

• f is Ω -stable,

• f CR-stable,

• f is hyperbolic on the chain recurrent set.

Moreover, in these conditions the homeomorphism h is almost identical and the equality Ω(f)=CR(f) takes place. Thus, to check Ω-stable or CR-stable we have to verify hyperbolicity on the chain recurrent set. We show that the use of symbolic image (definition see below) lets us to verify hyperbolicity.

Hyperbolicity

Let Λ be an invariant set of f. The diffeomorphism f is said to be hyperbolic on Λ if there exist invariant subbundles E^s and E^u of the tangent space TM|_Λand constants d>0 and α>0 that

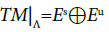
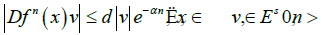
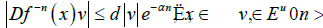
The invariance of subbundles E^s,u means 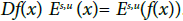The invariant subbundles E^s and E^u are named stable and unstable, correspondingly. The condition 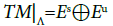means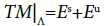 and E^s∪E^u=0 The constant α is named the exponent of hyperbolicity.

It is extremely difficult to verify the hyperbolicity conditions on a chain-recurrent set in a general case.

Lyapunov exponents and chain-recurrent components on projective bundles

The differential Df(x)=(∂f/∂x) defines a linear extension of system (1),

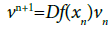
to the tangent bundle TM. Every nondegenerate linear mapping A: R^d→R^d can be represented in the form

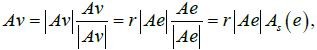
Where, = 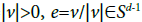and Sd-1 is the unit sphere. Thus, the linear mapping

A: v→ Av is the product of two mappings: 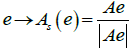and r→r|Ae|

where the first of them acts on the sphere S^d-1 and the other acts on the positive half-line R⁺.

The projective space P^d-1 can be obtained by identifying antipodal points of the sphere S^d-1. The symmetry of the mapping As(e) with respect to the sign change A_s(±e)= ±A_s(e) enables us to define a mapping

PA(e)=Ae/|Ae|

onto the projective space P^d-1 by identifying the antipodal points on the sphere. We preserve the notation e for the points of the space P^d-1, i.e., e stands for the one-dimensional subspace and (or) a unit vector on the subspace, which does not lead to confusion. Thus, we obtain the mapping

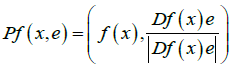(2)

on the projective bundle 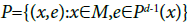, and this mapping generates a discrete dynamical system of the form

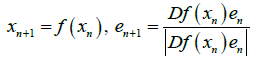(3)

on the projective bundle P. The positive number a(x,e)=|Df(x)e| is the coefficient of length change on the subspace e.

Recall that, if 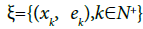is an ε-semitrajectory of the mapping Pf, then the number

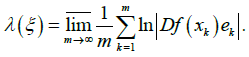
is the Lyapunov characteristic exponent of this semitrajectory [9]. Let 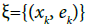be a p-periodic pseudo-trajectory; then the Lyapunov exponent of ξ is the arithmetic mean over the period

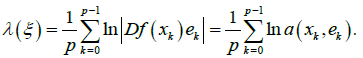
Definition 4

The spectrum of differential is defined as follows:

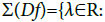there are periodic ε_k-trajectories ξ_k that ε_k→0, λ(ξ_k)→λ as k→∞}

Thus, the spectrum of differential is the limit set of Lyapunov exponents of periodic ε-trajectories as ε→0.

The spectrum of differential is often called the Morse spectrum [10,11]. As was proved [10], the spectrum of differential coincides with the limit set of Lyapunov exponents of all ε-trajectories as ε→0. As follows from results of Chap. 12 of the book [11] every component Ω of the chain-recurrent set CR(Pf) generates in the spectrum an interval 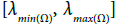where λ_min(Ω) and λ_max(Ω) are the least and the greatest Lyapunov exponents of the periodic pseudotrajectories of the component Ω. These intervals can have nontrivial intersection for distinct components of the chain-recurrent set CR(Pf) [10]. Every component Ω_ik of the chain-recurrent set CR(Pf) on the projective bundle P is projected to some component Ω_i of the chain-recurrent set CR(f) on the manifold M. The number of chainrecurrent components on M is not bounded; however, the number of components Ω_ik ⊂ P that are projected onto a chosen component Ω_i ⊂ M does not exceed the dimension of the manifold M [11]. The next theorem let us reduce the verification of hyperbolicity to calculation of the spectrum of differential.

Theorem 2

The following statements are equivalent [11]:

• the diffeomorphism f is hyperbolic on the chain recurrent set CR(f),

• the spectrum of the differential Df does not contain 0.

Symbolic Image

A method which enables one to construct the spectrum with an arbitrary accuracy was described in [11-13]. The corresponding technique combined symbolic dynamics [14,15] and numerical methods [16]. The method uses the notion of symbolic image of a dynamical system.

Definition 5

Consider a finite closed covering C={M(1),…,M(n)} of a domain M. The set M_i is called a cell of index i. Let G be the directed graph with the vertices {i} corresponding to the cells {M(i)}. Vertices i and j are connected by a directed edge (an arc) i→j if and only if [17].

f(M(i))∩M(j)≠∅ (4)

The graph G is called the symbolic image of the mapping f for the covering C.

The symbolic image is a geometric tool used to discretize a dynamical process. The investigation of the symbolic image enables one to obtain useful information concerning the global structure of the dynamical system. The symbolic image depends on the covering C, and its modification modifies the symbolic image. The existence of an edge i→j ensures the existence of a point x in the cell M(i) that f(x) ∈ M(j) In other words, the edge i→j is the track of the passage x→f(x), where x∈ M(i), f(x) ∈ M(j) If the edge i→j does not exist, then there are no points x∈ M(i) that f(x) ∈ M(j). Let the covering C consist of cells that are parallelepipeds intersecting along boundary disks. From this covering we shall construct a partition C*={M*(i)} attributing the boundary disks to only one of the neighboring cells; here we choose the notation C for the covering by closed parallelepipeds and write C* for the corresponding partition.

Definition 6

A two-sided infinite sequence {z_k} of vertices of the graph G is called an admissible path (or simply a path) if, for every k, G contains the directed arc z_k → z_k+1.

Let diam M(i)=max(ρ(x,y) : x, y ∈M(i)) be the diameter of the cell M(i). Denote by

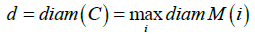
the diameter of the covering C. There is a natural correspondence between the admissible paths on the symbolic image G and ε-rajectories of the mapping f.

Theorem 3

(Shadowing property) [11]

1. If a sequence {z_k} is an admissible path on a symbolic image G, then there is a sequence of points {x_k}, x_k ∈M(z_k), which is an ε-trajectory of f for every ε>d.

In particular, if the sequence {z₁,z₂,…,z_p} is p-periodic, then the ε-trajectory {x₁,x₂,…,x_p} is p-periodic.

2. If a sequence of points {x_k} is an ε-trajectory of f, where ε is sufficiently small and xk ∈M(z_k), then the sequence {z_k} is an admissible path on the symbolic image G.

In particular, if an ε-trajectory {x₁,x₂,…,x_p} is p-periodic, then {z₁,z₂,…,z_p} is a p-periodic path on G.

Roughly speaking, an admissible path is the track of an -trajectory, and conversely. Thus, a path on the symbolic image can be regarded as an encoding of trajectories.

Definition 7

A vertex of a symbolic image is said to be recurrent if there is a periodic path passing through this vertex. Denote the set of recurrent vertices by RV. Recurrent vertices i and j are said to be equivalent if there is a periodic path passing through i and j.

The set of recurrent vertices RV is partitioned into equivalence classes {H_k} In graph theory, the classes H_k are called strongly connected components. We shall apply the process of subdivision of coverings and construct a sequence of symbolic images.

Consider the main step of the process of subdivision. Let C={M(i)} be a covering, and let G be the symbolic image for C. Suppose that a new covering NC is a subdivision of the covering C. This means that every cell M(i) is subdivided into cells m(i, k), k=1,2,…, i.e.,

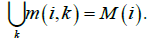
Denote by NG the new symbolic image for the covering NC={m(i, k)}. The vertices of NG are denoted by (i, k). This construction generates a mapping s from NG to G which takes the vertices (i, k) to the vertex i. Since from

f(m(i, k))∩m(j,l)≠ ∅

it follows that

f(m(i, k))∩m(j)≠ ∅

and thus the arc (i, k) →(j, l) is mapped onto the arc i→j. Hence s takes the directed graph NG onto the directed graph G. Therefore, every admissible path on NG is transformed by the mapping s onto some admissible path on G. In particular, the image of a periodic path is a periodic path, and the image of a recurrent vertex is a recurrent vertex. Moreover, the image of a class NH of equivalent recurrent vertices on NG is in the class H of equivalent recurrent vertices on G.

Denote by p(d) the union of cells M(i) for which the vertex i is recurrent, i.e.,

p(d)={∪ M(i): i is a recurrent vertex}, (5)

where d stands for the diameter of the covering. Suppose that C=C₀ is the original covering and C₁, C₂,… are obtained by the above process of subdivision, and the sets P₀, P₁, P₂,… are constructed according to (5).

Theorem 4

(Localization of the chain-recurrent set) [18].

The sequence of sets P₀, P₁, P₂,… has the following properties:

1) every P_k is a closed neighborhood of the chain-recurrent set;

2) if the diameters d_k of the coverings satisfy the condition d_k→0, then

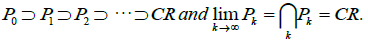
Computation of the Spectrum

Now we apply the symbolic image construction to the mapping Pf(x,e). Let G(f) be a symbolic image of the mapping f with respect to a covering C(M)={m(1),…,m(s)}. To construct a symbolic image of the induced mapping Pf: P→P it is convenient to choose a covering C(p)={M(z)} of the projective bundle P which conforms with the covering C(M) so that the projection of each cell is a cell:

p(M(z))=m(j).

Let G(P(f) be a symbolic image of the mapping Pf for the covering C(p)={M(z)}. Let us construct a framing of the symbolic image as follows. Choose a point (x_i, e_i) in every cell M(i) and write

b[ij]=In|Df(x_i)e_i|

for every arc i →j. Obviously, such a point is not unique. If a point (x*,e*)∈M(i) is another point, we have

|ln|Df(x*)e*|-ln|Df(x_i)e_i||=η(d),

where η(d) is a modulus of continuity of the function ln|Df(x)e| and d is the maximal diameter of cells of the covering C(P).

Definition 8

The pair a symbolic image G(Pf) and {b[ij]}is called a labeled symbolic image G_lb.

For any p-periodic path ω = {z₁,...,z_p=z₀} on G(Pf) the number

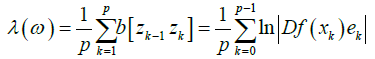
Is called a characteristic or Lyapunov exponent of the periodic path ω.

The spectrum of the labeled symbolic image G_lb is defined as

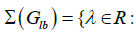there are periodic paths ω_k that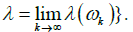

Let H be a class of equivalent recurrent vertices. A periodic path ω = {z₁,...,z_p=z₀} is called simple if the vertices z₁,...,z_p are different. Since a symbolic image has a finite number of vertices, the number of simple period paths is finite. For the class H let {φ₁,φ₂,…,φ_q} be all simple periodic paths. Let

λ_min (H)=min{λ(φ_j),j=1,...,q},

λ_max (H)=max{λ(φ_j),j=1,...,q},

be the minimum and the maximum of characteristic exponents for simple periodic paths of the class H. There is an algorithm [19] that determines λ_min (H_k)and λ_max (H_k).

Theorem 5

1) The spectrum of the labeled symbolic image Σ(G_lb) consists of the intervals [17].

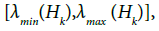
Where {H_k} is the full family of classes of equivalent recurrent vertices of the symbolic image G(Pf).

2) The spectrum of the differential is Σ(Df) in the extended spectrum of the labeled symbolic image

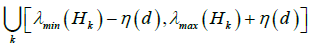
where by {H_k}is the full family of classes of equivalent recurrent vertices on the symbolic image G(Pf), d is a maximal diameter of cells of the covering C(P), η(d) is a modulus of continuity of ln|Df(x)e|.

3) A diffeomorphism f is hyperbolic on the chain recurrent set CR(f) if and only if there exists d₀>0 that the extended spectrum of the symbolic image for a covering C(P) with maximal diameter d<d₀ does not contain 0.

Theorem provides a way for the verification of hyperbolicity on the chain-recurrent set. For this purpose, it is necessary to build a covering projective bundle of a rather small diameter. However, we have no estimate of the maximal diameter d₀. So, the verification of structural stability should be achieved by the construction of a sequence of symbolic images applying a subdivision of coverings. The verification of hyperbolicity of the Ikeda type mapping has been described [11].

Structural Stability

Definition 9

A diffeomorphism f is said to be structurally stable if for any ε>0 there exists δ>0 that the inequality ρ₁(f,g)<δ implies the existence of a homeomorphism h: M→M that hf=gh and ρ₀(h,id)<ε where id is the identity mapping.

Structural stability of the system means that the dynamics is invariable under small perturbations, which makes the results of the study practically applicable, since a mathematical model is always only approximation of the real system. Therefore, it is very important to have conditions that allow us to verify structural stability constructively. It is also desirable that sufficient and necessary conditions were close and constructive and could be represented in the form of computer programs.

The first classical result gained by of A.A Andronov and L.S Pontryagin in 1937 describes the conditions for the structural stability of differential equation systems on a plane. In the 1980s, J. Robin, C. Robinson, and R. Manet found necessary and sufficient conditions for structural stability However, these conditions are of abstract nature and of practical little use. Our goal is to transform these conditions into equivalent but algorithmically verifiable ones.

Transversality Condition

For x ∈ M let TM(x) be the tangent space of M at x. The stable S(x) and unstable U(x) subspaces at x are defined as

S(x) ={v ∈ TM(x): |Dfn(x)v|→0 as n→∞},

U(x)={v ∈ TM(x): |Dfn(x)v| →0 as n→-∞}

We say that the transversality condition is fulfilled on M if

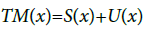
for any x ∈ M

Summarizing the results of Robbin et al. [20], Robinson et al. [21], and Mane et al. [22] we obtain the following theorem [23].

Theorem 6

A diffeomorphism f is structurally stable if and only if the transversality condition is fulfilled on M.

Thus, the theorem describes a necessary and sufficient condition. However, the application of this result is limited by the difficulties in verifying the transversality condition.

Let the transversality condition be fulfilled and diffeomorphism f be hyperbolic on an invariant set Λ. Then invariant subspaces E^s (x) и E^u (x) continuously depend on о�?�? x∈Λ and

dim E^s +dim E^u=dim M.

Consequently, on each connected component of the set Λ dimensions of subspace E^s и E^u are constant. The differential contracts exponentially on Es and exponentially extends on E^u. It is clear that E^s (x) ⊂ S(x) and Eu (x) ⊂ U(x). The following theorem shows that these subspaces coincide over a chain-recurrent set, that is, E^s (x)=S(x) and E^u (x)=U(x), x ∈ CR.

Theorem 7

If the transversality conditions are fulfilled, then [2,22]

1) Λ={x∈ M:TM(x)=S(x)⊕U(x)} is closed and invariant,

2) f is hyperbolic on Λ and и E^s (x)=S(x), E^u (x)=U(x), x ∈ Λ

3) the chain recurrent set CR is in Λ.

Complementary Differential

As was mentioned above, verification of the transversality condition involves great difficulties, and in the general case, there is no algorithm for checking this condition.

The differential Df: TM → TM is a natural example of a linear extension of the mapping f. Consider another example of a linear extension - the dual differentia Dˆ f , which is defined as follows.

Let 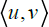denote the scalar product and an A-linear mapping, then the conjugate mapping A* is defined by the equality

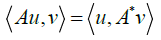
If A is a matrix, then A*is a transposed matrix. The matrix (A*)^-1 is inverse to the transposed one. In this case, the operations of transposition and inversion of the matrix can be interchanged.

Complementary differential is defined as follows:

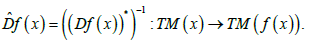
Actually, the complementary differential acts in the dual space TM* which is identified with TM. By definition, the complementary differential covers f. The main property of the complementary differential is that the inner product persists under the action of the differential and the complementary differential:

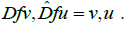
Complementary differential Dˆ f generates a dynamical system of the form

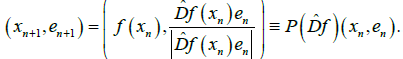(6)

The hyperbolicity of the dual differential is defined the same as of the differential.

Theorem 8

A diffeomorphism f is hyperbolic on a chain-recurrent set CR(f) if and only if the dual differential Dˆ f is hyperbolic on CR(f) [2,24].

Spectrum of the complementary differential 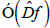is determined as the spectrum of averaging of the function

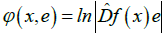
over periodic pseudo-trajectories of the system (6):

let ω={(x_k,e_k ),k=1,2,…,p} be a periodic ε-trajectory of the system (6),

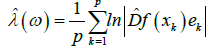
Consider the covering C(P) of the projective bundle and construct a symbolic image 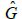of the mapping 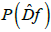. Choosing the points (x_i,e_i) in each cell M(i), we construct the framing 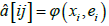of 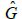. We can find the spectrum 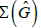of a framed symbolic image and its extension using the modulus of continuity of the function 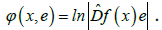The next theorem is an analog of theorems 2 and 4.

Theorem 9

The following statements are equivalent.

• A diffeomorphism f is hyperbolic on the chain-recurrent set CR(f).

Complementary differential Dˆ f is hyperbolic on the chainrecurrent set CR(f).

The spectrum of the complementary differential 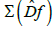does not contain 0.

there exists d0>0 that the extended spectrum of the symbolic image of P(Dˆ f ) for a covering C(P) with maximal diameter d<d0 does not contain 0.

Definition 10

The complementary differential is said to have only trivial bounded trajectories if any bounded trajectory

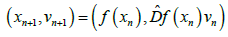
is a zero trajectory, i.e. v_n=0.

The following theorem describes the transversality condition in terms of the dual differential (see Proposition 8.46 [2]).

Theorem 10

The transversality condition is fulfilled on M if and only if the complementary differential has only trivial bounded trajectories [2,23].

At first glance, it seems that to verify the described property of the dual differential is just as difficult as to verify the transversality condition. However, we shall show that it is possible to verify the absence of non-trivial bounded trajectories of the dual differential using the symbolic image of the mapping .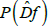

It should be emphasized that hyperbolicity on the chain recurrent set may be verified by the spectrum of the differential or the complementary differential. However, to verify the transversality condition on a non-recurrent set, we have to apply the complementary differential.

Suppose the spectrum of the dual differential does not contain zero, then 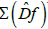consists of two parts: the positive part Σ+ and the negative part Σ-. The spectrum consists of segments, each of which is generated by a component of a chain-recurrent set. In this connection, the chain-recurrent set 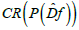of the mapping 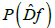is divided into two parts CR⁺ and CR^- so that 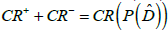and the spectrum of restriction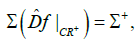

but the spectrum of restriction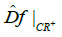

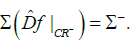
We call the sets CR⁺ and CR^- positive and negative chain-recurrent sets of the dual differential on the projective bundle P, respectively.

Attractor and Repeller

An invariant closed set Λ is called attractor for f if there exists a neighborhood U of Λ that

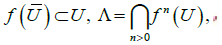
the set U is called the absorbing neighborhood of Λ. The set

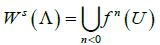
is named basin or domain of attraction. An invariant closed set Λ is repeller for ð�?�? if Λ is attractor fo^r f^-1. If Λ is an attractor for f, the set

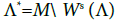
is a repeller which is called dual repeller for Λ and the pair Λ, Λ* is called attractor-repeller pair. Thus the dynamics between an attractorrepeller pair is very simple: each trajectory starts at the repeller and ends at the attractor. One can say that each trajectory through [25].

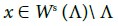
starts at the repeller Λ* and ends at the attractor Λ. As might be expected, the properties of the attractor and its domain of attraction hold not only for true trajectories, but they also can be applied to ε -trajectories.

Attractor on symbolic image

Consider a symbolic image G of a homeomorphism f. A set of vertices L is named invariant if for each vertex i ∈ L there is an admissible path through i which lies in L. Let L be an invariant set on G The set of vertices

En(L)={j∈L: there exists an edge iâ�?¶ j, i∉ L}

is called entrance of L. The set of vertices

Ex(L)={i∈L: there exists an edge iâ�?¶ j, j∉L}

is called exit of L. We say that an invariant set L is attractor on G if Ex(L)=∅, and an invariant set L is repeller if En(L)=∅. Let L be an attractor. A basin or domain of attraction is the set of vertices

D(L)={j: each path through j ends in L}.

It is well known if L is an attractor and D(L)is its basin then the set of vertices L*=Ver(G)\D(L) is dual repeller, where Ver(G) is the set of vertices of G [11].

The directed graph G is uniquely determined by its (adjacency) matrix of transitions

Π =(π_ij),

Where π_ij=1if and only if there is the directed edge i→j otherwise π_ij=1. It is well known [11] if L is an attractor and L* is dual repeller then the vertices of a symbolic image G can be renumbered so that the transition matrix takes the form

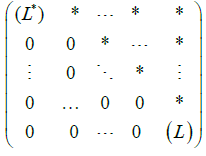
where the blocks (L*) and (L) correspond the repeller L*and the attractor L respectively, zeros are under diagonal, units may be over diagonal only.

The following theorem shows that both an attractor of a dynamical system and its domain of attraction can be constructed as precisely as one likes through a symbolic image, being its diameter small enough.

Theorem 11

If L and D(L)are attractor and its domain of attraction on a symbolic image G, then there are an attractor Λ of the homeomorphism f and its basin Ws(Λ) such that [11].

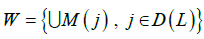
where into denotes the interior, is an absorbing neighborhood of Λ,

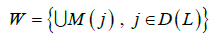
is an approximation of the basin Ws(Λ) such that W⊂W^s(Λ)

Theorem 12

Let Λ be an attractor, V₁ be its arbitrarily small neighborhood, and V₂ be an arbitrarily large neighborhood such that [11].

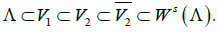
Then there exists d₀>0 such that each symbolic image G with the maximal diameter of covering cells d<d₀ has an attractor L and a domain of attraction D(L) so that

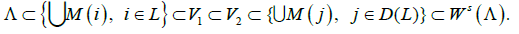
Equivalent Conditions

Theorem 13

The complementary differential has only trivial bounded trajectories if and only if the unstable manifold Wu (CR⁺) is an attractor and the stable manifold W^s (CR^-) is its dual repeller [2,26].

We say that there exists a connection

CR⁺→CR^-

CRif there is a trajectory χ of 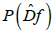such that its α-limit set α(χ) is in CR⁺ and its ω-limit set ω(χ) is in CR^-.

If the dual differential has only trivial bounded trajectories, then from Theorem 11 it follows that there exist trajectories going from W^s(CR^-) to W^u (CR⁺), and there are no trajectories going back from W^u(CR⁺) to W^s(CR^-) . Since CR⁺⊂ W^u (CR⁺) and CR^- ⊂ W^s(CR^-), there are no trajectories from CR⁺ to CR^-, i.e. there is no connection CR⁺→CR^-.

Theorem 14

A diffeomorphism f is structurally stable if and only if the spectrum of the complementary differential does not contain 0 and there exists no connection CR⁺→CR^-.

Proof 1: Sufficiency. Suppose that the spectrum 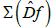of the dual differential does not contain zero and there is no connection CR⁺→CR^-. According to Theorems 6 and 10, in order to prove the structural stability, it suffices to show that the dual differential has only trivial bounded trajectories.

If the spectrum of the dual differential does not contain 0, then the chain-recurrent set 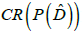of the mapping 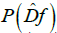is divided into two parts CR⁺ and CR^-. Since the spectrum 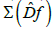is closed, there exists a segment [-β ,β ],β>0 which does not contain points of the spectrum. Let χ=(x_k,v_k-)}be a nonzero trajectory of the dual differential 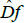and 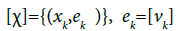is the projection of the trajectory χ onto the projective bundle p. Let E(χ)={(x_k,E_k)}, where E_k is a one-dimensional subspace spanned by vk, then E(χ) is a onedimensional bundle over [χ].

If [χ] is a chain-recurrent trajectory, then [χ] lies in CR++CR-, and hence χ is hyperbolic and unbounded. Suppose [χ] is not a chain-recurrent trajectory. Then its ω-limit set ω([χ]) lies in some component of the chain-recurrent set 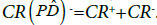The same is true for the α-limit set α([χ]). We say that [χ] starts in CR⁺ if its α-limit set α([χ])⊂CR⁺; [χ] starts in CR^- if its α-limit set α([χ])⊂CR^-. Similarly, [χ] ends in CR⁺ if ω([χ])⊂CR⁺; [χ] ends in CR- if ω([χ])⊂CR^-.

Let [χ] end in CR+. Then the trajectory exponent λ(χ)≥β>0 and the positive semitrajectory χ+ is unbounded. Similarly, if [χ] ends in CR-, then the exponent λ(χ)≤-β <0 and the positive semitrajectory χ+ is bounded. In the same way, if [χ] starts in CR+, then the negative semitrajectory χ- is bounded, and if [χ] starts in CR-, then the negative semitrajectory χ- is unbounded.

Consequently, the non-zero trajectory χ is bounded if and only if [χ] starts at CR⁺ and ends in CR^-. In this case we have the connection CR⁺→CR^-. This contradicts the condition. Hence, it is necessary that the trajectory χ be unbounded. Thus, any nonzero trajectory of the dual differential is unbounded. Then Theorems 6 and 10 imply that the diffeomorphism f is structurally stable.

2 Necessity. Suppose f is structurally stable. According to Theorems 6 and 7, the diffeomorphism F is hyperbolic on the chain-recurrent set CR(f). By Theorem 9, the spectrum of the dual differential does not contain zero and, as it is closed, it does not contain a segment [-β ,β ],β>0. The spectrum is divided into two parts positive Σ⁺ and negative Σ-. Similarly, the chain-recurrent set CR(P(Dˆ f ))of the dual differential on the projective bundle also splits into two parts CR⁺ and CR, in correspondence with the partition of the spectrum. According to Theorem 10, the dual differential must have only trivial bounded trajectories. The connection CR⁺→CR^- generates the trajectory of the mapping P(Dˆ f ) from CR⁺, CR- which in turn generates a trajectory χ of the dual differential Dˆ f with a negative exponent on the positive semitrajectory and a positive exponent on the negative semitrajectory. In this case, χ is a bounded trajectory, which leads to a contradiction. Hence, there is no connection CR⁺→CR^-.

The theorem is proved.

Structural Stability Verification

Consider methods of verification the above conditions. Let the mapping

F(x,v)=(f(x),A(x)v)

is a linear extension of the mapping f on the tangent bundle TM. In our case, 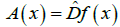. Let G(f) be a symbolic image of f for the covering C(M)={m(1),… ,m(q)}. Denote the PF mapping of the form:

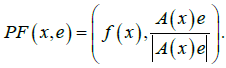
To construct the symbolic image of the induced mapping PF:P→ P, it is convenient to choose the covering C(P)={M(z)} of the projective bundle P compatible with the covering C(M) so that the projection of the cell on P is a cell on M: π (M(z))=m(j). In this case, the compatible coverings generate a natural mapping h from G(PF) onto G(f): h(z)=j As the inequality

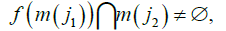
results in

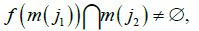
then the edge z₁→ z₂ on G(PF) is taken to the edge j₁→j₂ on G(f) by the mapping h Hence, the mapping h maps an riented graph G(PF) onto an oriented graph (f)

Consider the symbolic image G of the dual differential on the projective bundle 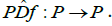Suppose that the spectrum of the dual differential does not contain zero. Then there exists d₀>0, such that for any covering C(P) of the projective bundle of the diameter d<d₀ (according to Theorem 9) the extended spectrum of the symbolic image does not contain zero. Each class of equivalent recurrent vertices H_k of the symbolic image ˆG receives an extended spectral interval

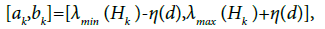
which is positive for a_k>0 or negative for b_k<0. Denote by H⁺ the union of classes with positive intervals H⁺={â�?�?H_k , b_k>0} and H⁺={â�?�?H_k, b_k<0}with negative intervals. It is natural to call the sets H⁺ and H^- as positive and negative classes of recurrent vertices. It is known that the set

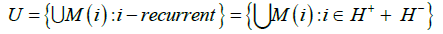
is a closed neighborhood of a chain-recurrent set. In particular, the set

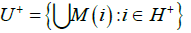
is a neighborhood of CR⁺ and the set

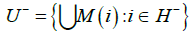
Is a neighborhood of CR^-.

We‘ll consider that on a symbolic image G there exists a connection H⁺→H^- if there exists a path from H⁺ to H^- on G.

Theorem 15

A diffeomorphism f is structurally stable if and only if there exists d₀>0 such that for any covering C(P) with diameter d<d₀ the extended spectrum of symbolic image G(PDˆ f ) of the complementary differential does not contain 0 and there is no connection H⁺→H^-.

Proof 1. Sufficiency. Let there exist d₀>0, such that for the covering C(P) of the projective bundle of the diameter d<d0, the extended spectrum of the symbolic image G(PDˆ f ) of the dual differential does not contain zero and there is no connection H⁺→H^-. Let us fix the described covering and construct a symbolic image. Then according to Theorem 9 the spectrum of the dual differential does not contain zero, and the dual differential is hyperbolic on the chain-recurrent set CR(f), and the set

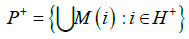
is a neighborhood of CR⁺ and the set

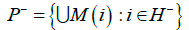
is a neighborhood of CR-. Since there is no connection H⁺→H^- on G, there is no connection CR⁺→CR^-. From Theorem 14 it follows that the diffeomorphism f is structurally stable.

2. Necessity. Let the diffeomorphism f be structurally stable. Then from Theorem 14 it follows that the spectrum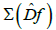 of the dual differential does not contain zero and there is no connection CR⁺→CR^-. From Theorem 9 it follows that there is d₁>0, that the extended spectrum of the symbolic image of the dual differential for the covering of the projective space C(P) with the maximum diameter d<d₁ does not contain zero. The classes of equivalent recurrent vertices are divided into positive and negative H⁺ and H^-, so that

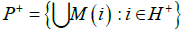
is a neighborhood of CR⁺ and the set

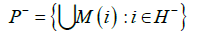
is a neighborhood of CR^-. It follows from Theorem 13 that the unstable manifold W^u(CR⁺) is an attractor on the projective bundle P, and the stable manifold W^s(CR^-) is its dual repeller. It follows from Theorem 12 that there exists d₂>0 such that each symbolic image of G corresponding to a covering with the maximum cell diameter d<d₂ has an attractor L⁺ and a dual repeller L^- such that

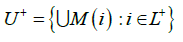
is a closed neighborhood of 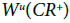and

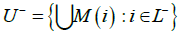
is a closed neighborhood of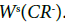

The set U⁺ is an absorbing neighborhood for the attractor W^u(CR⁺) and U^- is a repelling neighborhood for the dual repeller W^s(CR^-), the trajectories going from U^- to U⁺. If we choose d⁰=min(d₁,d₂), and d<d₀, then there exist an attractor L⁺ and a dual repeller L^- on the symbolic image described above. In this case, the matrix of permissible transitions is reduced by renumbering the vertices to the form

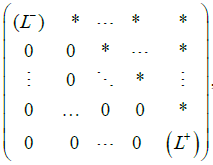
where there are zeros under the diagonal, zeros along the diagonal correspond to transient vertices, the diagonal blocks L^- and L⁺ correspond to the vertices L^- and L⁺, and there may be zeros or ones above the diagonal. With such a transition matrix, there is the only transition possible from L^- to L⁺. Since H⁺⊂ L⁺, H^-⊂ L- there is no path from H⁺ to H^- on the symbolic image.

The theorem is proved.

Thus, structural stability can be verified by the following method

1) Choose a covering C of the manifold M and construct a symbolic image G(f) of the mapping f;

2) Define the recurrent vertices on G(f) and localize the chainrecurrent set of the mapping f [27-29];

3) The dual differential Dˆ f is constructed: TM →TM;

4) The covering C(P) of the projective bundle P is chosen and construct a symbolic image G(PDˆ f ) of the mapping PDˆ f

5) Define the recurrent vertices on G(PDˆ f ) and localize the chain-recurrent set of the mapping PDˆ f [27-29];

6) A framed symbolic image G is constructed for the mapping P(Dˆ f ): P→ P ;

7) The extended spectrum of the symbolic image ˆG is determined [19];

8) If the extended spectrum does not contain zero, then the positive and negative sets of return vertices H⁺ and H^- are determined;

9) The connection H⁺→ H^- is verified.

If there�?�? is no such a connection, then the diffeomorphism f is structurally stable.

It follows from Theorem 15 that if we apply the method of sequential subdivision so that the maximum diameter d_k→ 0, then a finite number of subdivisions will satisfy the inequality d_k < d₀ and the described algorithm will verify the structural stability when it takes place.

Test to verify H⁺→ H_- connection

Let us assume that the spectrum of the dual differential does not contain zero and H⁺ (H^-) is the union of classes forming the positive (negative) part of the spectrum. Our goal is to check whether there is a path from H⁺ to H^-. Let �?�? be a set of vertices, and the vertex I outside �?�? is an entrance in �?�? if there exists an arc i i→j j, where the vertex j∈ �?�?. If there is no exit from the invariant set of vertices �?�? , then �?�? is an attractor on the symbolic image.

The algorithm to verify H⁺→ H^- connection.

1. Let us mark all the vertices of the set �?�? = H⁺

2. Check if there is an exit from �?�?. If there is no exit, then �?�? is an attractor and as H⁺⊂ �?�?, then there is no connection H⁺→ H^- , and the algorithm is complete.

3. If there is an exit i from �?�? then we can go along any path ω = {i,…} to the vertices of the sets �?�? and H^-.

4. As all recurrent vertices lie in �?�? and H^-, the path ω can end in �?�? and H^-, all the vertices of ω except the first and the last ones being non-recurrent.

5. If ω ends in H-, it determines the connection �?�? → H^-, and since H⁺⊂ �?�?, and there exists a path from H⁺ to any vertex �?�?, then there is a connection H⁺→ H^- , and the algorithm is complete.

6. If the path ω ends in �?�?, then we mark all the vertices of the path ω and include them in �?�?. Then we proceed to step 2.

After a finite number of steps, we either find the connection H⁺→ H^-, or we construct the attractor �?�? which includes H⁺ and excludes H^- , that guarantees that there is no connection H⁺→ H-. The number of steps of the algorithm is estimated by the number of non-recurrent vertices.

Acknowledgement

This work was financially supported in part by the Russian Foundation for Basic Research under grant 16-01-00452.

References

1. Palis JJ, Melo WD (2012) Geometric Theory of Dynamical Systems: An Introduction. Springer Science & Business Media, New York, USA.
2. Bronshtein IU (1984) Nonautonomous dynamical system. Shtinisa, Kishinev.
3. Pilyugin S Yu (1994) The Space of Dynamical Systems with the C0-Topology. Springer, New York, USA.
4. Sharkovsky AN (1977) Structure theory of differentiable dynamical systems and weak nonwandering points. Abt Math Naturwiss Techn 4: 193-200.
5. Shub M (1978) Stabilite globale de systems denamiques. Asterisque 56: 1-21.
6. Andronov AA, Pontryagin LS (1937) Rough Systems. Doklady Academy Nauk 14: 247-250.
7. Smale S (1970) The Ω stability theorem. Pure Math 14: 289-97.
8. Franke J and Selgrade J (1977) Hyperbolicity and chain recurrence. J Differential Equations 26: 27-36.
9. Lyapunov AM (1992) The general problem of the stability of motion. Int J Control 55:531-534.
10. Colonius F, Kliemann W (2012) The dynamics of control. Springer Science & Business Media, Boston, USA.
11. Osipenko G (2006) Dynamical systems, graphs, and algorithms. Springer, New York, USA.
12. Osipenko GS (2000) Spectrum of a dynamical system and applied symbolic dynamics. J Math Anal Appl 252: 587-616.
13. Osipenko GS, Romanovsky JV, Ampilova NB, Petrenko EI (2004) Computation of the Morse spectrum. J Math Sci 120: 1155-1166.
14. Lind D, Marcus B (1995) An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, UK.
15. Robinson C (1995) Dynamical Systems. Stability, Symbolic Dynamics and Chaos.CRC Press, Boca Raton, FL, USA.
16. Hsu CS (1987) Cell-to-Cell Mapping: A Method of Global Analysis for Nonlinear Systems. Springer, New York, USA.
17. Osipenko GS (1983) On a symbolic image of dynamical system. Boundary value problems, Interuniv. Collect sci Works, Perm, Russia.
18. Osipenko GS (1994) Localization of the chain recurrent set by symbolic dynamics methods. Proceedings of Dynamic Systems and Applications, Dynamic Publishers Inc, Atlanta, GA, USA.
19. Georgiadis L, Goldberg AV, Tarjan RE, Werneck RF (2009) An experimental study of minimum mean cycle algorithms. Proceedings of 6th International Workshop on Algorithm Engineering and Experiments, New Zealand.
20. Robbin JW (1971) A structural stability theorem. Ann Math 1: 447-493.
21. Robinson C (1976) Structural stability of C1-diffeomorphism. J Diff Equat 22: 28-73.
22. Mane R (1977) Characterizations of AS diffeomorphisms. Lect Notes Math 597: 389-394.
23. Mane R (1988) A proof of the C1-stability conjecture. Publ Math Inst Hautes Etud Sci 66: 161-210.
24. Sacker R, Sell G (1974) Existence of dichotomies and invariant splitting for linear differential systems I. J Diff Eq 15: 429-458.
25. Bhatia NP, Szego GP (1970) Stability theory of dynamical systems. Springer. New York, USA.
26. Salamon D, Zehnder E (1988) Flows on vector bundles and hyperbolic sets. Trans Amer Math Soc 306: 623-649.
27. Pissanetzky S (1984) Sparse Matrix Technology. Academic Press. New York, USA.
28. Tarjan R (1972) Depth-First Search and Linear Graph Algorithms. SIAM J Comput 1: 146-160.
29. Tarjan R (1983) Data structures and network algorithms. SIAM, Philadelphia, USA.