Review Article, J Nucl Ene Sci Power Generat Technol Vol: 11 Issue: 3
State of Charge Estimation by Using an Unscented Kalman Filter for Lead Acid Battery
Prasanna Mishra1*, N. Archana2
1Department of Automobile Engineering, PSG College of Technology, Coimbatore, Tamil Nadu, India
2Department of Electrical and Electronics Engineering, PSG College of Technology, Coimbatore, Tamil Nadu, India
*Corresponding Author: Prasanna Mishra, Department of Automobile Engineering, PSG College of Technology, Coimbatore, Tamil Nadu, India, Tel: 9490303888; E-mail: prasannamishra234@gmail.com
Received date: 25 February, 2022, Manuscript No. JNPGT-22-45684;
Editor assigned date: 01 March, 2022, PreQC No. JNPGT-22-45684(PQ);
Reviewed date: 14 March, 2022, QC No. JNPGT-22-45684;
Revised date: 21 March, 2022, Manuscript No. JNPGT-22-45684(R);
Published date: 24 March, 2022, DOI: 10.4172/2325-9809.1000261
Citation: Mishra P, Nivedetha B (2021) Enhancing Security in Wireless Sensor Networks. J Nucl Ene Sci Power Generat Technol 11:3
Abstract
Electric Vehicles have several potential advantages over traditional internal combustion engine vehicles. They promise zero emission and efficiency. State of charge of a battery is considered as one of the important parameters of lead acid battery. Study has been done and identified that temperature is a main factor that affects the state of charge of the battery and some measures are to be taken to improve its performance. Unscented kalman filter plays a vital role in estimating the real state of charge of a lead acid battery. Testing of lead acid battery has been done in real-time. Unscented kalman filter code is implemented in MATLAB environment and the state of charge has been estimated for the degrading battery.
Keywords: Lead acid battery; State of Charge (SOC); Unscented Kalman Filter (UKF)
Introduction
An absorbed Glass Mat (AGM) battery is a type of valve-regulated lead-acid (VRLA) battery, which is designed for low-maintenance rechargeable batteries. Absorbent glass mat batteries are same as that of lead-acid battery but the electrolyte is held in glass mat separators, as opposed to freely flooding the plates. This design brings significant advantages to AGM batteries such as purer lead, water conservation, fluid retention, high power density, lower internal resistance that allow the batteries being charged or discharged more quickly. As a result, the voltage performance of AGM during charging and discharging is slightly different from conventional lead-acid batteries. Factors like temperature, sulfation and ageing affects the battery life.The purpose of this work is to study the factors affecting the battery State of Charge (SOC) and find a solution to determine the accurate value of the state of charge of the lead acid battery for electric vehicle (two-wheeler) using unscented kalman filter.
Literature Survery
The lead storage battery is the most conventional and the most widely applied storage battery in the world today. Applications for these vary from small sealed batteries of a few Watt-hours capacity in consumer applications to large batteries of many megawatt-hours capacity in submarines, utilities, and other applications. The reaction products at the electrodes on charge and discharge of a lead-acid storage battery are given in the “double sulfate theory”. The enthalpy, Gibbs free energy and its temperature coefficients for this chemical reaction have been the subject of many discussions. Because the concentration of sulfuric acid is appreciably changed by the conversion, numerous investigations of its thermodynamics have been carried out. Since 1954 these studies have been extended by two important findings: The discovery of two forms of PbO2, α- PbO2, β- PbO2, in the active materials leads to alterations in the value of the thermodynamic quantities. The free energies of the two modifications of PbO2 differ slightly, whereas the entropies are quite different. The electrochemistry of the materials existing between defined phase limits (e.g., lead dioxide) can be explained [1]. The breadth of the phase influences the potential.
A lead acid battery uses a combination of lead plates or grids and an electrolyte consisting of a diluted sulfuric acid to convert electrical energy into potential chemical energy and back again. Each cell of a lead acid battery contains (in the charged state) electrodes of lead metal (Pb) and lead (IV) oxide (PbO2) in an electrolyte of about 37% w/w (5.99 Molar) sulfuric acid (strongSO4). In the discharged stateboth electrodes turn into lead (II) sulfate (PbSO4) and the electrolyte loses its dissolved sulfuric acid and becomes primarily water. Due to the freezing-point depression of water, as the battery discharges and the concentration of sulfuric acid decreases, the electrolyte is more likely to freeze. Because of the open cells with liquid electrolyte in most lead-acid batteries, overcharging with excessive charging voltages will generate oxygen and hydrogen gas by electrolysis of water, forming an explosive mix. This should be avoided. Caution must also be observed because of the extremely corrosive nature of sulfuric acid proposed by Wenxinpeng [2].
Lead acid batteries have lead plates for the two electrodes. Separators are used between the positive and negative plates of a lead acid battery to prevent short-circuit through physical contact, mostly through dendrites (treeing), but also through shedding of the active material. Separators obstruct the flow of ions between them and increase the internal resistance of the cell as proposed by Wenxinpeng [3]. The Extended Kalman Filter has been widely accepted as a standard tool in the machine learning community. In this paper we have presented an alternative to the EKF using the Unscented Filter (UKF).The UKF consistently achieves a better level ofaccuracy than the EKF at a comparable level of complexity. This has been demonstrated in a number of application domains, including state-estimation, dual estimation and parameter estimation [4].
In this paper, it is clearly explained how the unscented kalman filter providesbetter results than the Extended Kalman Filter (EKF) [4]. The electric lead-acid batteries are devices that provide the electric energy from chemical one. These are electrochemical generators. They store the energy that they restore according to the needs. They can be recharged when one reverses the chemical reaction; it is what differentiates them from the electric batteries [5]. In Thevenin battery model all the elements are assumed to be constant. Therefore this model is limited due to its dynamic accuracy as this model does not take account into the state of charge. This model can be used which do not consider the dynamic state of charge. Hence, it is not suitable for this project [6]. Voltage of lead-acid battery per cell produces 2 V. So battery 12 V consists of six cells, so that the next series. Voltage at the terminal will vary according to the conditions of work. And the concentration of the acid will be changed during the charge and discharge [7].
Battery performance and service life will be directly dependent on the quality and output characteristics of the charger selected. Currently, there are several battery charging control methods developed. Those methods are constant current with one-current rate and multiple decreasing current rate, constant voltage, two-step, three-step and pulse charging [8]. In the relationship between the discharge voltage and the SOC was determined for a wide range of discharge rates at different ambient temperatures for telecommunication backup power supply applications. However, since this relationship is not applicable to random discharge currents, this method has a large SOC error (up to 10%).
Methodology
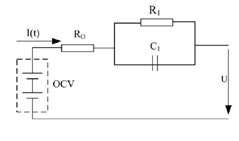
Figure 1: Proposed block diagram.
The block diagram proposed is shown in Figure 1.The proposed block diagram consists of lead acid battery in which the battery voltage, current are the input parameters given to the unscented kalman filter in addition with the process and measurement noise and then the battery state of chargeis estimated. This is then compared with the real SOC.
Battery equivalent circuit
The battery is considered as a source voltage that varies with their state of charge. This varies according to the current of the battery. If it is positive (battery discharge) then the state will decrease and discharge; if negative (battery charging) then the charge will increase [5].
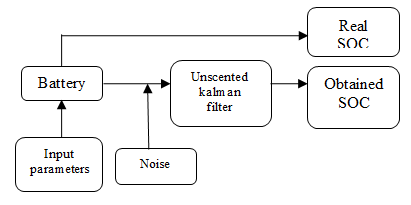
Figure 2: Equivalent circuit of a battery.
Battery equivalent circuit is studied at first order and second order model, as its model indicates that RC circuit may be connected in increasing orders. Increasing the order increases the complexity. The lead acid battery with single RC circuit indicates the first order model as shown in the Figure 2. The parameters are:
- Resistance R0 representing ohmic polarisation.
- Discharge over voltage resistance R1representing the charge transfer losses.
- Over voltage capacitance C1representing the double-layer effect dynamics.
- Open circuit electro-chemical potential OCV, representing the equilibrium emf of the battery under no load conditions.
State space equation of lead-acid battery
The lead acid battery first order RC input model as follows
= * + *i(K) (1)
And the RC output model can be expressed as
Y(K) = OCV *SOC (K) -U (K) –i(K)* R0 (2)
Unscented Kalman filter
The extended Kalman Filter (EKF) is the most widely applied state estimation algorithm for nonlinear systems. However, the EKF can be difficult to tune and often gives unreliable estimates if the system nonlinearities are severe. This is because the EKF relies on linearization to propagate the mean and covariance of the state.. The use of the UKF can provide significant improvement over the EKF.
The UKF addresses the approximation issues of the EKF. The state distribution is again represented by a Gaussian Random Variable (GRV) but is now specified using a minimal set of carefully chosen sample points. These sample points completely capture the true mean and covariance of the GRV. When a Gaussian is passed through a non-linear function, it does not remain a Gaussian anymore but we approximate the Gaussian from the resulting figure, so in UKF a process called unscented transform helps to perform this task. To summarize here are the steps the unscented transform performs:
- Compute set of sigma points
- Assign weights to each sigma point
- Transform the points through non-linear function
- Compute Gaussian from weighted and transformed points
- Compute mean and variance of the new Gaussian
Noise
Noise is said to be the disturbance that affects the performance of the lead acid battery. There are two types of noises namely process noise and measurement noise. Measurement noise is that sensor noise from sensors like voltage sensor, current sensor and temperature sensor. The methodology followed to estimate the SoC is shown in Figure 3.
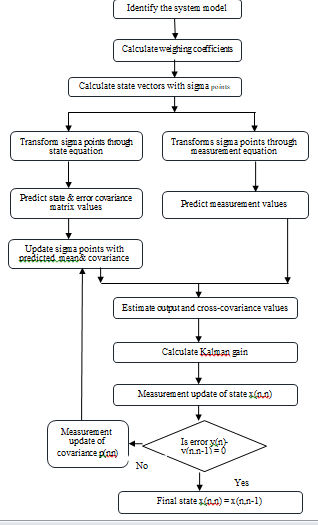
Figure 3: Flow chart of the proposed system.
Results and Disscussion
Unscented kalman filter code is implemented in MATLAB software for estimating the state of charge of lead acid battery [9]. Here the second order battery state space model has been taken. Graph has been plotted for the Battery state of charge (%) with respect to sampling time (in hours) with the constant current discharge of 8 Amps for 12 V battery as shown in the Figure 4. Similarly, Battery Output voltage is plotted with respect to sampling time for the degrading lead acid battery with the constant current discharge of 8 Amps for 12 V battery as shown in the Figure 5. Fully charged battery is taken and the value of SoC for fully charged battery is 100% and input voltage is 13.5 aretaken as an initial states and the UKF helps to estimate the future values of SoC for the respective output voltage at a constant current discharge of 8 amps as shown in the Figure 6. For best approximation, UKF has been chosen and the estimated output is almost same as that of real value and the % error between real value and estimated output is shown in the Figure 7.
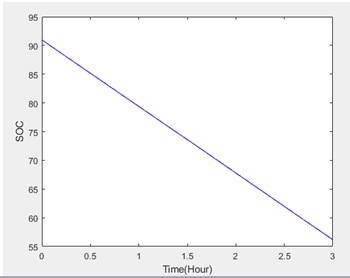
Figure 4: SoCvs time.
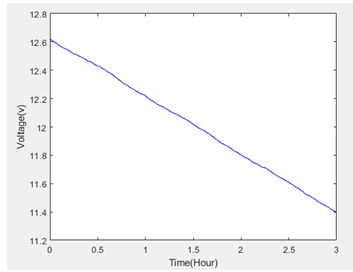
Figure 5: Output voltage vs time.
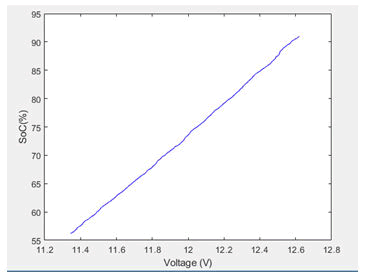
Figure 6: SoC(%) vs output voltage(v).
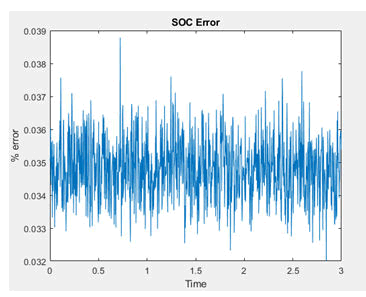
Figure 7: Error between estimated and real values.
Conclusion
The factors affecting the lead acid battery has been studied and the mathematical model of unscented kalman filter is studied. When compared to the extended kalmanfilter, the unscented kalman filter gives a better approximation because EKF may not give a better value for highly non-linear functions. Experimentallythe battery is tested with constant load and the state of charge is determined. Unscented kalman filter is implemented in matlab and the state of charge is estimated for a given degrading battery and compared with the real value. In future, UKF can be implemented using hardware unit.
References
- Xuyun F, Zechang S (2008) A battery model including hysteresis for state-of-charge estimation in Ni-MH battery. IEEE Vehicle Power Propul Confer.
- Singhal S, Wu L (1988) Training multilayer perceptrons with the extended Kalman algorithm. Adv Neural Informat Process Syst 1: 133-140.
- Sun F, Hu X, Zou Y, Li S (2011) Adaptive unscented Kalman filtering for state of charge estimation of a lithium-ion battery for electric vehicles. Energy 36: 3531-3540.
- He Z, Gao M, Wang C, Wang L, Liu Y (2013) Adaptive state of charge estimation for Li-ion batteries based on an unscented Kalman filter with an enhanced battery model. Energies 6: 4134-4151.
- Huang C, Wang Z, Zhao Z, Wang L, Lai CS, et al. (2018) Robustness evaluation of extended and unscented Kalman filter for battery state of charge estimation. IEEE Access 6: 27617-27628.
- Gholizade-Narm H, Charkhgard M (2013) Lithium-ion battery state of charge estimation based on square-root unscented Kalman filter. IET Power Electron 6: 1833-1841.
- Tian Y, Xia B, Sun W, Xu Z, Zheng W (2014) A modified model based state of charge estimation of power lithium-ion batteries using unscented Kalman filter. J Power Source 270: 619-626.
- Aung H, Low KS, Goh ST (2014) State-of-charge estimation of lithium-ion battery using square root spherical unscented Kalman filter (Sqrt-UKFST) in nanosatellite. IEEE Trans Power Electron 30: 4774-4783.
- Chen Z, Yang L, Zhao X, Wang Y, He Z (2019) Online state of charge estimation of Li-ion battery based on an improved unscented Kalman filter approach. Appl Mathemat Model 70: 532-544.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi