Research Article, Res Rep Math Vol: 2 Issue: 4

Sufficient condition of the Hopf bifurcation

Amine Bernoussi^*

Department of Mathematics, Faculty of Science, Ibn Tofail University, Kenitra, Morocco

*Corresponding Author : Amine Bernoussi
Department of Mathematics, Faculty of Science, Ibn Tofail University, BP 133, 14000, Kenitra, Morocco
E-mail: amine.bernoussi@yahoo.fr

Received: September 15, 2018 Accepted: December 04, 2018 Published: December 11, 2018

Citation: Bernoussi A (2018) Sufficient Condition of the Hopf Bifurcation. Res Rep Math 2:4

Abstract

Keywords: Hopf bifurcation; Local stability bifurcation the hopf; Differential equations

Introduction

In this paper, we propose the following sufficient condition for the local Hopf bifurcation for a differential equation system with delay the form:

The initial condition for the above system is

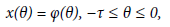
with φ=(φ₁, φ₂, φ₃) where φ_i∈C(i=1,2,3), such that φ_i(θ) ≥ 0(-τ≤θ≤ 0,i=1,2,3). Here C denotes the Banach space C([-τ,0]R) of continuous functions mapping the interval [-τ,0] into R, equipped with the supremum norm. The non-negative cone of C is defined as C+= C([-τ,0], R⁺), where R⁺={x∈ R|x ≥ 0}. We here assume that f: R³→ R is a locally Lipschitz continuous function on R³ Suppose that the equation (1) has a equilibrium point P*; and the characteristic equation of the equation (1) around the equilibrium point P* takes the general form:

With

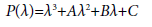
and

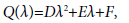
The main results are as follows

Theorem 1 (Amine Bernoussi) Assume that the equilibrium P* of system (1) is locally asymptotically stable for τ=0:

If 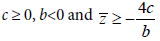Then there exists a positive τ₀ such that, when τ∈[0,τ₀) the steady state P* is locally asymptotically stable, and a Hopf bifurcation occurs as τ passes through τ₀; where τ₀ is given by

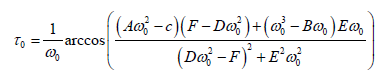
and ω₀ is the least simple positive root of equation (5), and c, b and ͞z are defined in lemma 2 and equation (5). further we have

The organization of this paper is as follows. In section 2, we offer basic results for the prove of theorem 1. In section 3, we establish the local asymptotic stability and the Hopf bifurcation of the equilibrium P* and prove theorem 1. Finally a discussion and conclusion is offered in section 4.

Basic Results

We offer some basic results for the prove of theorem 1. Now we return to the study of equation (2) with τ>0. Equation (2) has a purely imaginary root iω, with ω>0:

Δ(iω, τ)=0

if and only if

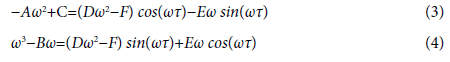
Squaring and adding the squares together, we obtain

with 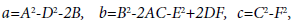where A, B, C, D, E and F are given by (2).

Letting z=ω², equation (5) becomes the following cubic equation

Lemma 2 [5] Define

(i) If c < 0, then equation (6) has at least one positive root.

(ii) If c ≥ 0 and Δ ≤ 0, then equation (6) has no positive roots.

(iii) If c ≥ 0 and Δ>0, then equation (6) has positive roots if and

only if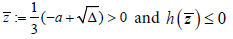

From lemma 2, we have the following lemma.

Lemma 3 Assume that the equilibrium P* of system (1) is locally asymptotically stable for τ=0

(i) If one of the following:

(N1) c ≥ 0, and Δ ≤ 0,

(N2) c ≥ 0, Δ>0, and ͞z ≤ 0,

(N3) c ≥ 0, Δ>0, and h( ͞z )>0,

is true, then all roots of equation (2) have negative real parts for all τ ≥ 0.

(ii) If c<0, or c ≥ 0, Δ>0, ͞z >0, and h( ͞z )≤ 0, then all roots of equation (2) have negative real parts when

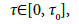
where Δ and ͞z >0 are defined in lemma 2

Sufficient Condition of the Hopf Bifurcation

In this section, we establish the condition sufisent of the Hopf bifurcation of the equilibrium P*.

Theorem 4 Assume that the equilibrium P* of system (1) is locally asymptotically stable for τ=0.

If 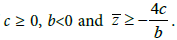Then there exists a positive τ₀ such that, when τ∈[0, τ₀) the steady state P* is locally asymptotically stable, and a Hopf bifurcation occurs as τ passes through τ₀, where τ₀ is given by

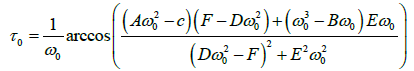
and ω₀ is the least simple positive root of equation (5), and c, b and z are defined in lemma 2 and equation (5). further we have

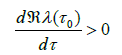
Proof. Consider the equation

the discriminant Δ1 of the equation (8) is given by

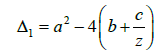
or by the hypothes c ≥ 0 and therefore equation (8) admits two solutions

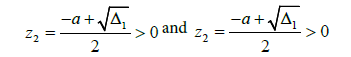
then we have

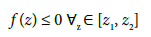
the hypotheses 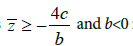implies that Therefore

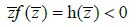
On the other since from the hypotheses b<0 then Δ>0 then the hypotheses (iii) of the Lemma 2 is satisfied. Hence the equation (6) has at least one positive solution, more Lemma 3 implies that all roots of equation (2) have negative real parts when τ [0, τ₀).

Now we will determine τ₀.

Without loss of generality, we assume that the equation (6) has three positive roots, denoted by z₁, z₂ and z₃, respectively.

Then equation (5) has three positive roots, say

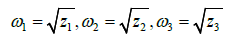
According to equations (3) and (4) we have

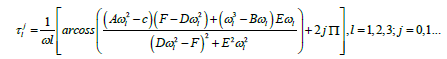
Then ±iωl is a pair of purely imaginary roots of equation (2) with 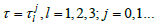clearly,

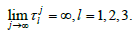
Thus, we can define

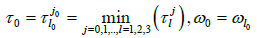
Next we need to guarantee the transversality condition of the Hopf bifurcation theorem [1-4].

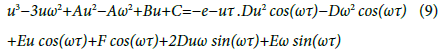
And

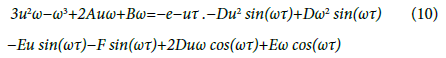
Let u(τ) and ω(τ) satisfying u(τ₀)=0, and ω(τ₀)=ω₀. By differentiating the equations (9) and (10) with respect to τ and then set τ=τ₀. Doing this, we get

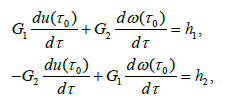
Where

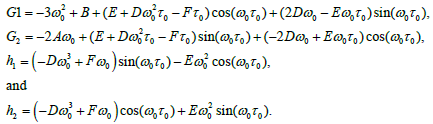
Solving for 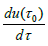we get

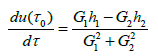
Therefore we have

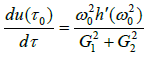
Note that if 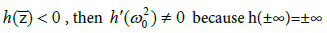h(0)=c≥0.

Thus if 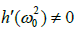we have the transversality condition:

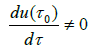
If 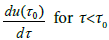and close to τ₀, then equation (2) has a root λ(τ) = u(τ)+iω(τ) satisfying u(τ)>0, which contradicts (ii) of Lemma 3. This completes the proof.

Remark 5 Our main result also valid for any differential equation of higher dimension three provided that the study of the characteristic equation of the equation reduces to study the equation (2) and more generally all the problems in Rⁿ has equation of the form [5-7]:

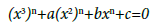
Conclusion

In this work, we presented a mathematical analysis for a nonlinear autonomous differential equation with delays in three dimensions. The originality of this work is to have a new sufficient condition for the Hopf bifurcation of equilibria. On the other hand, the main results can be generalized to differential equation of dimension greater than three (see Remark 5).

References

1. J.K. Hale and S.M. Verduyn Lunel, Introduction to Functional Differential Equations, Springer- Verlag, New York, 1993.
2. B. D. Hassard, N. D. Kazarinoff, and Y. H. Wan, Theory and Applications of Hopf Bifurcation. Cambridge: Cam- bridge University Press.
3. Y. Kuang; Delay Differentiel Equations With Applications in Population Dynamics, Aca-demic Press, INC., New York 1993.
4. Shigui Ruan, Junjie Wei, On the zeroes of transcendental functions with applications to the stability of delay differ- ential equations, Journal Dynamics of continuous, discrete and impulsive systems, SER. A: Mathematical Analysis. volume, 10. PP. 863–874. 2003.
5. S. Ruan, J. Wei, On the zeros of a third degree exponential polynomial with applications to a delayed model for the control of testosterone secretion. IMA J. Math. App. Med. Biol. 18, 41?52,2001.
6. R. Xu ; Global dynamic of a delayed epidemic model with latency and relapse, Nonlinear Analysis : Modelling and control, 2013 ,vol.18,No.2,250-263 436-444.
7. R. Xu ; Global dynamics of an SEIRI epidemiological model with time delay, Applied Math- ematics and Computa- tion Volume 232, 1 April 2014, Pages 436-444.