Research Article, J Fashion Technol Textile Eng Vol: 6 Issue: 1
Surface Characterization of Cashmere Fabrics Using Optical and Transient Thermal Properties
Narantogtokh Davaajav and Sachiko Sukigara*
Department of Advanced Fibro-Science, Kyoto Institute of Technology, Kyoto, 606-8585 Japan
*Corresponding Author : Sachiko Sukigara
Professor, Department of Advanced Fibro-Science, Kyoto Institute of Technology, Kyoto, 606-8585 Japan
Tel: +81-75-724-7365
Fax: +81-75-724-7365
E-mail: sukigara@kit.ac.jp
Received: December 12, 2017 Accepted: January 19, 2018 Published: January 26, 2018
Citation: Davaajav N, Sukigara S (2018) Surface Characterization of Cashmere Fabrics Using Optical and Transient Thermal Properties. J Fashion Technol Textile Eng 6:1. doi:10.4172/2329-9568.1000165
Abstract
Fine hairs on a cashmere fabric (i.e., its hairiness) generate its softness, warmth, and unique luster. To make cashmere more popular, we require value-adding elements and quality specification to develop new clothing products. In this study, a surface characterization method was examined to specify the effect of hairs on the softness, luster, and warmth of cashmere fabrics. The luster was measured using a goniospectrophotometer as the fabric was rotated. A high CIELAB L* was found for rotation angles θω around 90°, corresponding to an aligned fiber surface, but not for random fiber assemblies. The shape of the plot of L* versus θω was affected by the degree of hairiness and its direction. By measuring the surface roughness (SMD) with a surface tester, a difference in light reflection between the warp and weft directions of the fabric was observed according to the hairiness direction. Fabric surfaces with smaller values of SMD showed larger values of L*. These surface hairs and hairiness were also observed clearly as differences in the surface friction. For the transient heat flux (qmax) related to the warmth perception, hairier samples showed lower values than did less hairy samples.
Keywords: Cashmere fabrics; Luster; Warm touch; Goniospectrophotometric measurement
Introduction
Woven cashmere fabrics are well known as high-grade luxury fabrics because of their softness, light weight, warmth, and unique luster. Cashmere fibers are increasingly popular in the current textile market, being used for knitwear, coats, scarves, and gloves. Fine cashmere yarns are also used for worsted fabrics. Cashmere is also blended with wool, silk, and other natural fibers to create fabrics of differing quality and to control the price [1]. To increase the popularity of cashmere, value-adding elements and quality specification are required to develop new value-added clothing products.
The mechanical and tactile properties (known as the fabric hand) of cashmere have been reported at the levels of fiber [2], yarn [3], and fabric [4]. However, for cashmere coats, the fabric luster, which is related to the surface hairs is yet to be considered.
The luster of woven cashmere fabric is likely to become an important value-added component as far as consumers are concerned because how light is reflected from the fabric surface can influence its visual impression. Visual evaluation of the appearance of a fabric changes according to the light source, the direction from which the light strikes the fabric, and the angle at which the fabric is viewed [5–7]. We have developed a method whereby a goniospectrophotometer measures the overall specular and diffuse reflection of a rotating fabric [8,9]. This method proved capable of distinguishing between fuzzsurface and clear-finish wool fabrics. Herein, we applied the same method to differentiate between fine cashmere hairs on fabrics.
The surface of fine hairs might influence the warm/cool feeling as well as the light reflection of cashmere fabrics. Kawabata et al. [10] interpreted the warm/cool feeling when fabric touches skin as a peak value of the heat flux (qmax). Tu et al. [11] found that qmax was influenced by differences in surface roughness, surface fuzz, and moisture regain. Therefore, qmax could be used to characterize the cashmere hairs on a fabric.
An aim of the present study is to find the unique light reflection properties of cashmere coat fabrics related to surface hairiness. Also, the relationship among the lightness (L*) distribution, surface roughness, and qmax is investigated to apply fabric finishing aimed at value-added fabric design.
Experimental Details
Samples
We chose 10 black woven cashmere and wool fabrics used to make lightweight coats with which to investigate the effect of fine hairs on surface characterization. The sample specifications are given in Table 1, and surface photographs captured by a digital microscope (VHX-900; Keyence, Japan) are shown in Figure 1. Samples C1–C3 were woven with the same yarn count (16 × 1 tex) but were finished by three different companies. The weave structure of each cashmere sample was 3 × 1 twill. The same raw cashmere (fineness 15.77 μm, length 44.4 mm) was used for all cashmere samples except C4. The difference in surface hairiness was observed covering weave structure (Figure 1). Also shown in Figure 1 is the surface hairiness of the wool samples W1–W4; sample W4 had less hair on its surface, allowing the weave lines to be seen more clearly.
| Sample | Structure | Fiber | Yarn count (tex) | Weave density ( / cm) | Weight (g/m2) | Thickness (mm) | Dyeing | ||
|---|---|---|---|---|---|---|---|---|---|
| warp | weft | ends | picks | ||||||
| C1 | 3 × 1 twill | cashmere | 16.0 × 1 | 30 | 17 | 286 | 1.51 | ||
| C2 | cashmere | 16.0 × 1 | 25 | 16 | 282 | 1.48 | Top | ||
| C3 | cashmere | 16.0 × 1 | 30 | 20 | 348 | 1.53 | |||
| C4 | cashmere | 14.5 × 1 | 14 | 12 | 260 | 1.70 | Top | ||
| C5 | cashmere | 14.0 × 1 | 26 | 24 | 298 | 1.55 | Top | ||
| C6 | cashmere | 14.0 × 1 | 26 | 23 | 318 | 1.30 | |||
| W1 | Broken twill | wool | 100 | 14 | 14 | 408 | 2.06 | Piece | |
| W2 | 2 × 1 twill | wool | 12.5 × 2 | 38 | 30 | 252 | 1.30 | Piece | |
| W3 | 2 × 2 twill (double cloth) | wool56, paper40, cotton4 | 16.6 × 2 | 20 × 1 | 60 | 64 | 428 | 3.18 | Top |
| W4 | 4 × 1 satin | wool | 13.8 × 2 | 40 | 27 | 214 | 0.46 | Top | |
Table 1: Sample specifications.
Measurements
Light reflectance
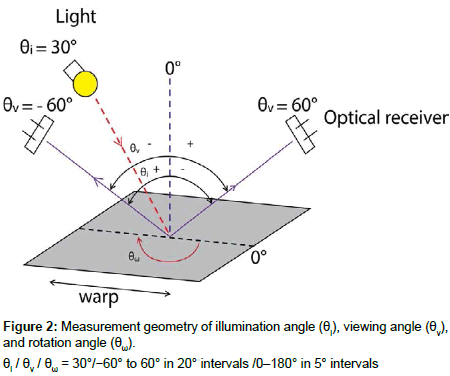
The light reflectance of each fabric sample was measured using a goniospectrophotometric color-measurement system (GCMC- 4; Murakami Color Research Laboratory Co., Ltd., Japan). The measurement geometry is shown in Figure 2. The effective lighting area was 4 × 2 cm to obtain the data. The measurements were carried out with different combinations of illumination angle θi, viewing angle θv, and rotation angle θω of the fabric. The rotation angle θω = 0 corresponds to the fabric warp direction. We investigated the following combinations of angles (denoted as (θi / θv / θω):
a) 30°/−60° to 60° in 20° intervals/0°, 45°, 90°;
b) 30°/−60°/0° to 180° in 5° intervals.
We determined the CIELAB L* values [12] by using a standard Illuminant D65 condition thereby obtaining spatial L* distributions from the reflectance data.
Surface friction and geometrical roughness
We measured the fabric surface friction using a surface tester (KES-SE-STP; Kato Tech. Co., Ltd., Japan). The contact sensor consisted of 10 parallel piano wires (each of 0.5 mm in diameter) to simulate human fingerprint. The sensor was placed on the surface of the fabric sample with an applied load of 0.49 N, and the sample stage was moved 5 cm at a speed of 1 mm/s. The mean coefficient of friction (MIU) and its deviation (MMD) were obtained [13].
We measured the surface geometrical roughness (SMD) [13] using a friction and roughness tester (KES-SE; Kato Tech. Co., Ltd., Japan). A U-shaped contactor consisting of a single piano wire (0.5 mm in diameter) was used over the fabric with a contact force of 0.1 N while the sample stage was moved 3 cm at 1 mm/s. We measured in three different locations both forward and backward in both the fabric warp and weft directions.
Peak value of heat flux (qmax)
The value of qmax is commonly used to predict the cool/warm feeling of a fabric. This value is influenced by the fabric surface. We measured the fabric qmax using a KES-F7 Thermolab II tester (Kato Tech. Co., Ltd., Japan) [10]. The heat stored in a copper plate (T-box, 3 × 3 cm, 9.79 g) was transferred to the fabric sample on a temperaturecontrolled stage at 20°C. The temperature difference between the specimen and the T-box was adjusted to be 10°C. The ambient conditions were a temperature of 20°C and a relative humidity of 60%.
Results and Discussion
Light reflection from fabric samples
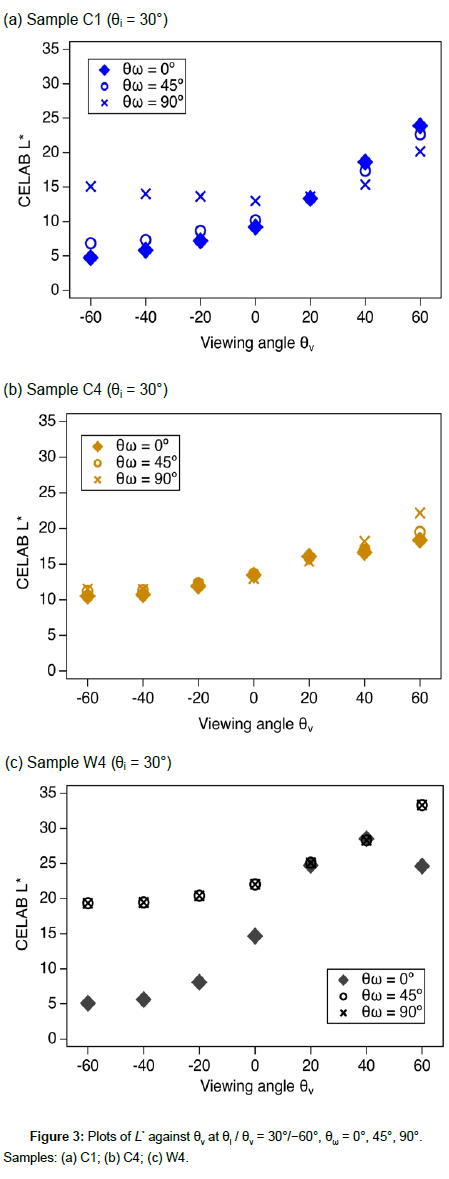
For a fabric, we consider that L* changing from light to dark or vice versa must be related to the nature of the surface hairs and the structure of the weave. In Figure 3, we plot L* against viewing angle (θv) at θi = 30° for θω = 0°, 45°, and 90°. Samples C1 and C4 were woven with a 3 × 1 twill weave using the same cashmere fibers, but the surface hairs on each fabric appeared differently, as shown in Figure 1. For all samples, the value of L* changed with θv.
The choice of θω affected L* in the range θv = −60° to 0° for samples C1 and W4. The difference in L* among the three values of θω was largest at θv = −60° for both samples (as seen in Figure 3a and 3c). The value of L* was independent of θω for sample C4. In our previous work, the weave structure was an important parameter determining how light reflected from worsted fabrics [8] and woven silk [9]. The difference between samples C1 and C4 is not due to their weave structure, so it must be due to their surface hairs. As shown in Figure 1, while the surface hairs of sample C1 are aligned well with the warp direction, those of sample C4 are tangled and disordered. This differing surface-hair morphology is reflected in the change of L* with θv. The rib weave of sample W4 is clearly observed in Figure 1, as is the fact that it is less hairy. For sample W4, changes in L* with θv could be indicative more of the weave structure than of the hairs.
For samples C1 and W4, the choice of θω (0°, 45°, or 90°) affected L* at viewing angles below 20°. Sample C1 with its hairy surface had higher L* values at θω = 90° than at θω = 45° or 0°. There was no difference in L* between θω = 0 and 45° for all viewing angles. In Figure 3, the effect of θω on L* becomes obvious at θv = −60°. Therefore, we used the distribution of L* to examine the effect of weave structure and surface hairs on the light reflection at θi / θv = 30°/−60°.
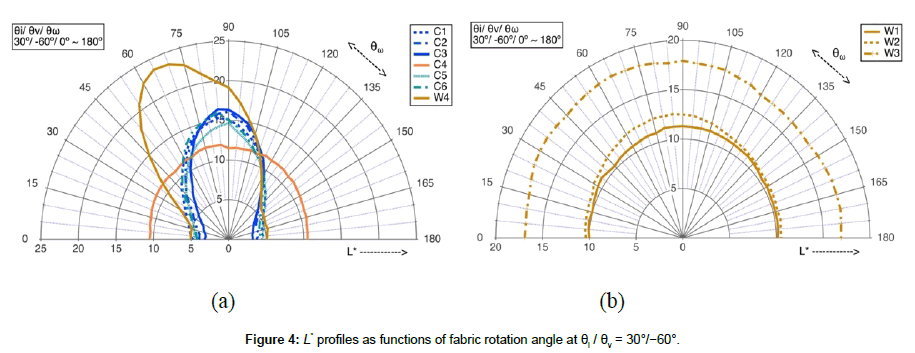
In Figure 4, the L* profiles for two groups of samples are shown as functions of the fabric rotation angle (θω) at θi / θv = 30°/−60°. The fabric is close to the warp direction at θω = 0° and the weft direction at θω = 90°. Changes in L* from light to dark or vice versa were clearly observed for these samples except for W4 in Figure 4a. In Table 2, the maximum and minimum L* values and corresponding θω values are listed for all samples. Samples C1–C3 showed maximum L* at θω = 90–95° and minimum L* at θω = 10°. The strongest contrast is seen for sample W4, with maximum L* = 23.61 and minimum L* = 5.02. This strong contrast observed for sample W4 results from a hairless satin weave structure.
| Sample | Maximum L* | θω maximum L* | Minimum L* | θω minimum L* |
|---|---|---|---|---|
| C1 | 15.4 | 90o | 4.47 | 10o |
| C2 | 16.11 | 95o | 3.75 | 10o |
| C3 | 16.48 | 90o | 3.08 | 10o |
| C4 | 11.97 | 80o | 10.45 | 10o |
| C5 | 14.65 | 95o | 4.37 | 0o |
| C6 | 16.06 | 90o | 4.05 | 0o |
| W1 | 11.3 | 90o | 9.97 | 5o |
| W2 | 12.58 | 90o | 10.37 | 5o |
| W3 | 18.08 | 60o | 16.44 | 155o |
| W4 | 23.61 | 60o | 5.02 | 5o |
Table 2: Maximum and minimum L* values and respective θω values
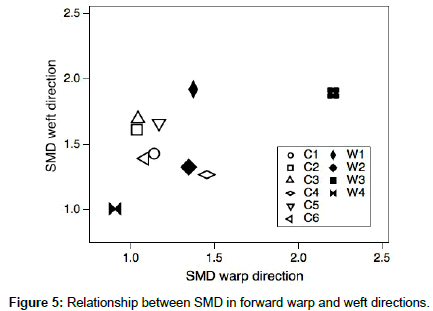
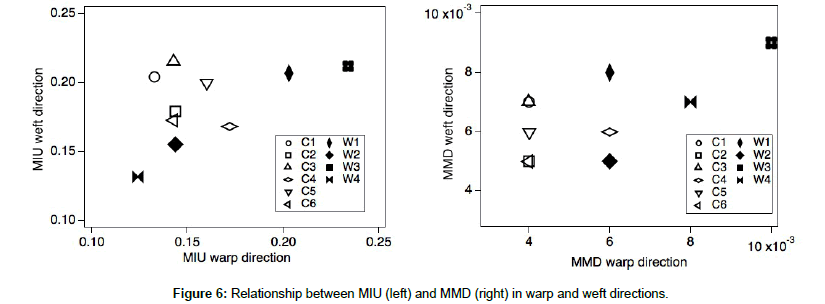
In Figure 5, the surface roughness (SMD) in the warp-forward direction is plotted against that of the weft-forward direction. The SMD values of the cashmere samples (C1–C3, C5, and C6) in the weft direction are larger than those in the warp direction. These cashmere samples had more fine fibers aligned with the warp direction (θi = 0), so this fine-haired surface structure gave a lower SMD value than that in the weft direction. However, sample C4 with the same 3 × 1 twill weave showed no difference in SMD values between the warp and weft directions. As shown in Figures 1 and 4, the surface hair morphology might have affected the SMD values too. Sample W4 had the lowest SMD values in both directions because of its clear weave structure with less hairiness compare to all the other samples. Therefore, the degree of surface hairiness or fuzz directly affected the SMD values.
The peak L* value and its profile were strongly influenced by fabric surface irregularity, which disperses light. The larger L* values of SMD are associated with smaller values of L*, so more light is dispersed from the surface.
In Figure 6, the mean coefficient of friction (MIU) and its mean deviation (MMD) in the warp direction are plotted against those in weft the direction. The MIU values of the cashmere samples (C1– C3, C5, and C6) in the weft direction were larger than those in the warp direction, especially for sample C3. Sample W4 with its clear weave structure on its surface showed the lowest MIU value of all the samples. With increasingly disordered surface hairiness, the MIU value increased for samples W2, C4, W1, and W3, respectively in ascending order.
The effect of fabric surface on the MMD values for samples C1– C3, C5, and C6 in the warp direction was lower than that in the weft direction and comparable with those of the other samples except W2. The aligned fine hairs on the fabric surface resulted in a smoother surface: for example, lower MMD values for samples C2 and C6 than for sample C4. The MMD values of the cashmere samples along the warp direction were smaller than those of wool samples W3 and W4.
Relationship between qmax and SMD
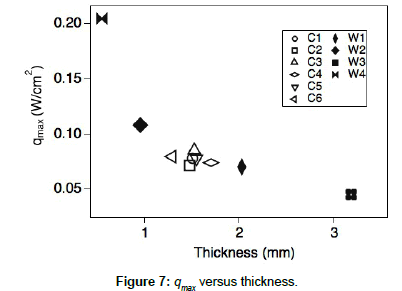
In Figure 7, the effect of heat flux (qmax) for all samples is plotted against fabric thickness. Sample W4 showed the highest qmax value because of its clear surface with fewer hairs. The qmax values of the cashmere samples range from 0.07 to 0.09 W/cm2, and the differences among the samples are very small.
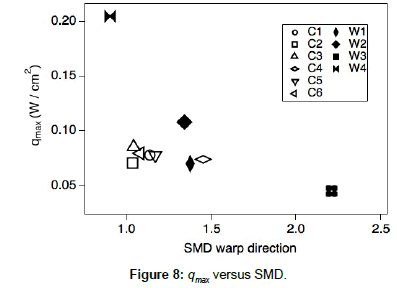
The values of qmax are plotted against the SMD values along the warp-forward direction in Figure 8. The SMD value of cashmere sample C4 was slightly larger than those of the other cashmere samples but was in the same range. Fine and soft cashmere hairs on the surface produced low values of qmax. Senoo et al. [14] measured qmax for 1.093 fabrics including those used for men’s winter suits and coats (fur). The average qmax for men’s winter suits was 0.167 ± 0.021 W/cm2, and that for coats was 0.147 ± 0.036 W/cm2. The qmax values for the cashmere samples used in this study were much smaller, so we expect a warmer feeling when they touch the skin.
The relationship between qmax and SMD obtained by the measurements for θi / θv = 30°/−60° at θω = 90–95° suggests that samples with fine hairs aligned on their surfaces show a peak in the L* distribution.
Conclusion
This study examined how surface hairs are related to light reflection from cashmere fabrics. When measurements were made for θi / θv / θω = 30°/−60°/90–95°, differing surface hair morphologies were found for cashmere fabrics. These differing surface hair morphologies were also confirmed by surface friction properties such as MIU, MMD, and geometrical roughness SMD.
The MIU values of cashmere fabrics with hairy surfaces in the weft direction were larger than those of samples that were less hairy in the warp direction. These differences between MIU, MMD, and SMD in the two directions agree with the difference in L* values between θω =90–95° and θω =10°. These surface properties and luster of cashmere caused by its hairiness can be altered by fabric finishing and could change the qmax value.
Acknowledgments
Davaajav Narantogtokh acknowledges the support of the Higher Engineering Education Development Scholar Program of the Mongolian Government (File No. M-JEED MON P-11). Special thanks are due to Gobi Co., Ltd. in Mongolia, who provided the cashmere fabric samples. This work was supported by JSPS KAKENHI Grant Number 15H01764.
References
- McGregor BA (2000) Recent advances in marketing and product development of Mohair and Cashmere.
- McGregor BA (2014) Variation in the softness and fiber curvature of cashmere, alpaca, mohair and other rare animal fibre. J Text I 105: 597-608.
- Wang X, Chang L, McGregor BA (2006) The hairiness of worsted wool and cashmere yarns and the inpact of fiber curvature. Text Res J 76: 281-287.
- Alimaa D, Matsuo T, Nakajima M (2000) Sensory measurements of the main mechanical parameters of knitted fabrics. Text Res J 70: 985–990.
- Lee W, Sato M (2001) Visual perception of texture of textiles. Color Res Appl 26: 469–477.
- Kanai H, Kimura H, Morishima M (2012) Microscopic photometry and its parameterization for objective evaluation of aesthetics of woven fabrics. Text Res J 82: 1982-1995.
- Hunter RS, Harold RW (1987) The measurement of appearance. (2nd edtn), John Wiley & Sons, Hoboken, New Jersey.
- Endo M, Kitaguchi S, Morita H, Sato T, Sukigara S (2013) Characterization of Fabrics using the Light Reflectance and the Surface Geometry Measurements, J Textile Engineering : 59: 75-81.
- Awazitani T, Sukigara S (2016) Charaterization of optical properties of traditional Japanese fabrics. Text Res J 86 : 13-23.
- Kawabata S (1984) Development of a Device for Measuring Heat Moisture Transfer Properties of Apparel Fabrics. J Text Mach Soc 37: T130-T141.
- Chendi Tu, Sachiko Sukigara (2017) Characterization of Wool Fabric Surface in terms of Transient Heat Transfer, J Fashion Technol Textile Eng: 5:3
- CIE Technical Committee (2004) CIE 015: Technical Report: Colorimetry, (3rd edtn), CIE Central Bureu, Vienna.
- Kawabata S (1980) The Standardization and analysis of hand evaluation. (2nd Edtn), Textile machinery society of Japan, Osaka, Japan.
- Senoo J, Yoneda M, Niwa M (1986) The Initial Maximum Value of Heat Flux (qmax) as an Objective Measure of Fabric Warm/Cool Feeling, J Home Econ 37: 1049-1061.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi