Research Article, J Neurosci Clin Res Vol: 3 Issue: 1

The Thermodynamic Analysis of Neural Computation

Deli E^1*, Peters JF² and Tozzi A³

¹Institute for Consciousness Research, Nyiregyhaza Benczur ter 9, Hungary

²Computational intelligence laboratory, university of Manitoba, Canada

³Center for nonlinear science, university of north Texas, 1155 union circle, 311427, Denton, TX 76203-5017, USA

*Corresponding Author : Eva Deli
Institute for Consciousness Research Nyiregyhaza Benczur ter 9, Hungary
Tel: 15073962613
E-mail: eva.kdeli@gmail.com

Received: January 25, 2018 Accepted: February 19, 2018 Published: February 27, 2018

Citation: Deli E, Peters JF, Tozzi A (2018) The Thermodynamic Analysis of Neural Computation. J Neurosci Clin Res 3:1.

Abstract

Keywords: Energy/information exchange; Information erasure; Entropy; Landauer’s principle; Carnot cycle; Deep learning

Introduction

The cortical brain is an evolutionary marvel which interacts with the outside world via self-regulation, based on its resting or ground state. The resting state, which is disturbed during stimulus and sensory processing, is recovered by automatic operations. In warm blooded animals, the brain’s energy need multiplies although, the human brain represents only 2% of the body weight it receives 15% of the cardiac output, 20% of totals body oxygen consumption, and 25% of total body glucose utilization. It is thought that baseline energy consumption has been almost exclusively dedicated to neuronal signaling [1]. This almost constant and huge energy use maintains the brain’s alertness, even during sleep by an active balance between inhibitory and excitatory neurons [2,3]. The slightest variation in excitation determines whether a spike is generated such a delicate balance of excitatory and inhibitory neurons turns the resting state into a highly energy requiring state [4-6]. Even in the absence of stimulus, the equal balance of excitatory and inhibitory neurons produces seemingly arbitrary bursts of resting state’s activation [7]. This active balance between contrasting influences ensures the brain’s ability for rapid, targeted response to environmental stimulus. For example, changes in inhibitory neurons increase frequencies and their energetic needs [4]. Via the sensory system, the brain partakes in the energy information exchange with the environment: the precarious energy balance turns interaction into a closed physical process: the thermodynamic entropy.

Entropy is a concept rooted in experience and experimental data different scientific fields (such as information theory or quantum mechanics) have their own, although related, definitions, with a significant amount of disagreement over diverse definitions of information and entropy [8,9]. To make just a few examples, it has been recently suggested that the negative work cost of erasure stands for negative entropy furthermore; entropy might drive order-increasing interactions, in closed systems and under special circumstances [10-12]. The brain’s resting state allows the considerations of stimulirelated energy changes, based on the laws of thermodynamics. Sensory activation is coupled to information increase via enhanced frequencies so that the brain’s energy/information cycle might form a closed thermodynamic system, similar to the Carnot cycle [13]. To gain better insight into the nature of entropy, here we investigate the role of stimulus during the entropic changes occurring during cognitive process. Landauer’s principle (i.e., the erasure of information produces a minimal quantity of heat, proportional to the thermal energy) shows that a certain amount of work is necessary to erase a bit of information, dissipated as heat to the environment [14]. The needed amount of work couples with the function of uncertainty about the system, because information about the system reduces the cost of erasure. Likewise, the information value of stimuli, which determines the extent of response, is highly subjective. For example, the correlation of neuronal activation with visual stimulus is dynamic and mediated by intracortical mechanisms [15]. Furthermore, the oscillation dynamics of local neurons reflect the anatomical/functional occurrence of intra-cortical feedback, thalamocortical network, global signal propagation, synaptic clustering, network states and other residual activities well beyond the sensory value of inputs [16]. Thus, the connection between information and ’work’ is the function of environmental entropy. Thus, applying Landauer’s principle to the brain’s cognitive process might uncover the thermodynamic nature of the energy information exchange during the sensory process.

One of the biggest puzzles in neuroscience is how comprehension and meaning emerge from the complex patterns of neural activity. Hemodynamic, metabolic parameters, membrane potential, electric spikes, neurotransmitter release have been studied [17-19]. EEG, lesion studies diffuse tensor imaging, MEG and fMRI analysis demonstrate that consciousness results from coherent, globally coordinated electric activities [20-25]. Since electric activities in the brain are correlated with conscious actions, the mind forms a unified experience by connecting sensory perception with mental states based on event related potentials [26,27]. An ensemble of cortical and subcortical regions, including the rostral anterior cingulate, precuneus, posterior cingulate cortex, posterior parietal cortex, dorsal prefrontal cortex, along with the caudate head, anterior claustrum and posterior thalamus, supports the occurrence and convergence of multiple resting state networks [28]. Resting state network convergence might facilitate global communication and underpinning systems level integration in the human brain [29]. Local electromagnetic potential differences in the complex neural landscape vary according to the principle of least action, forming metastable changes of spatiotemporal patterns that are isomorphic with cognitive and phenomenal occurrences [30]. Via recurring, highly reproducible harmonic functions the brain’s resting state has been shown to form the functional curvature of a four dimensional torus, which manifests itself as repetitive patterns of mental trajectories [31-35]. Even in the absence of synaptic anatomical connectivity, the resting state displays great autonomy and complexity, indicating its essential role as the ground state of the brain [36].

Biological organisms live with a temporal expiration date, determined by the access to air, water, food, mating, which modulates behavior between urgency and relaxation. The inner clock of activity is not connected to any local system, but results from a global temporal rhythm, which originates in midbrain dopamine neurons [37]. For example, sleep compresses the daytime firings of neurons in time. In fact, time turns into a relative experience, because intentional binding formulates the perception of time and gives rise to agency [38]. The importance of temporal considerations is further illustrated by the connection between deviations in time perceptions and diseases [39]. Major depression seems to slow time perception, whereas time passes at a jerky in schizophrenia [40]. Parkinson’s disease is characterized by impairment in time control, as well as time delay. Therefore, time perception an elementary part of the formation of conscious experience, might be regulated by the energy/information cycle of the brain. Understanding the brain’s energy/information exchange is critical, because disturbances in this cycle can cause health problems and disease without any obvious pathologic change in morphology.

The brain’s gradually improving responses to stimuli have molded organization into a coherent, structural, organizational mirror of physical systems [41]. However, biological survival needs, such as water, food, reproduction, etc. are being dictated by relativity in time, formed by an oscillating motivation between urgency and relaxation. Mental operations, which form an increasingly improving mirror of the social environment, constantly respond to the environment and modify it, forming their common evolution. This way, environmental abstraction becomes integral part of a wholesome mental world, engendering an interconnected system which determines and governs thoughts, intentions and behavior according to the laws of physics.

Discussion Theoretical Foundations

Stimuli provide information input that leads to a thermodynamic relationship with the environment, in the form of the electric activities of the neuronal network. Because all evoked oscillations are greater than electric activities of the resting state and accompanied by entropic and dimensionality changes, the brain’s information/ energy cycle between stimulus and recovery of the resting state can be analyzed based on thermodynamics. Stimulus generates heat that can be assessed in terms of enhanced frequencies, synaptic modification. That way, the brain’s responses to stimulus in the present state shapes its ability for future interactions. The energy devoted to neuronal connections satisfies Landauer’s principle, which reflects sensory interaction based on energy/information exchange. Evoked states are information saturated, thus produce high entropy and involve high frequencies; these high frequencies are unstable and, due to their huge energy requirement, become energetically untenable over time.

Because the sensory system transforms spatial information into the temporal language of the oscillations, the brain is organized along temporal coordinates [42]. Here we analyze the brain’s global energy/ information cycle in terms of entropic and topological considerations, in view of the correlation between physiology and electric activities. We achieve generalizations that allow the assessment of the relationship of the brain’s electric activities independent of their scale, magnitude, specific features and local boundaries-and cognitive experiences. We show that interconnected synaptic networks form a closed system, which leads to self-regulation based on energy/ information transformations satisfying the Landauer’s principle. Information accumulation corresponds to an increase in temperature indicated by enhanced frequencies, so that erasing information frees energy, which increases order through the energy accumulated in cortical synaptic connections. Therefore, self-regulation of activities is based on low entropy.

Brain activities do not exist in isolation; rather form a selfregulating, interconnected and coherent energy system. Moreover, brain models suggest that constantly changing nervous activities take place on different kinds of curvatures of the phase space [43]. Thus, activity can be assessed based on topological relationships. Topology suggests structures such as a toroidal view of activities and the projection of percepts to higher dimensional spaces as well as mappings of antipodal points on opposite perceived im- ages into hyperbolic manifolds [32]. Because disturbances in this self- regulating physical network might play a role in various pathologic conditions, we will take into account the relationship between temporal dimensionality and entropy, and the brain’s evoked energy/information exchange (interaction). Energy availability limits information processing in the brain.

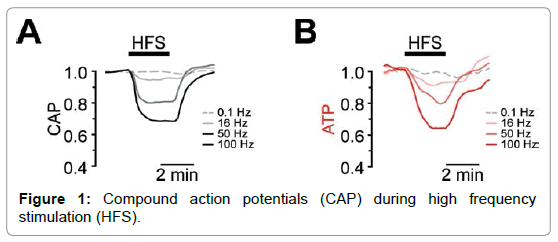
The consideration of living organisms as open systems has a long tradition in the literature. ATP is used as the main energy source for metabolic functions and thus it supplies the energy need of neural spiking activities. Around 45% of the brain’s baseline energy use in vivo is consumed on non-signaling processes [44,45]. In neurons, ATP consumption and ATP generation forms equilibrium between metabolic support and spiking activities. In an active brain, axonal ATP consumption is proportional to electric spiking activity. However, the expectation that the ATP production can satisfy liberally the energy need of signaling has been overturned. The surprising correlation between ATP levels and the generation of action potentials means that the increasing frequency of action potentials quickly deplete axonal energy levels [46]. This finding explains the existence of a complex energy supply network in neural tissue, in which multiple cell types and metabolic energy sources work in unison to maintain the ATP levels in axons. Nevertheless, nerve cells are unable to generate enough energy on their own to sustain their electrical activity. Axons depend on mitochondrial function to provide the necessary ATP levels. Both compound action potentials and axonal ATP content decrease in a stimulation frequency-dependent manner and ATP homeostasis actively relies on the presence of lactate. ATP decreases preceded or coincided with compound action potential decay confirm that energy depletion causes axonal failure. ATP supply in the white matter is limited and quickly depleted during cases of high frequency stimulation, such as, information processing in the brain (Figure 1). Because neurons cannot replenish their energy reserves fast enough during ATP depletion, e.g., such as in the case of high frequency activation, the brain’s information processing forms a closed system. Because high frequencies can only use the available (and highly limited) ATP supply, the path length of electric activity is proportional to the subjective information content of the stimulus and the ATP use is proportional to the path length. The limited axonal ATP supplies do not contribute to the processing of the stimulus any more than the ice melting to the sliding of the hockey puck. The low frequency response also has negligible energy use. Further- more, because sensory activation forms a closed loop around the resting state, the response must be complementary with the original stimulus in terms of entropy as well as temperature. For example, the temperature increase during stimulus must be complemented with a cooling down during sensory response. Therefore, path length represents the situation dependent energy need of information processing. The energy need of the maintenance of the readiness of the neural system is extremely high, because the noiseless spiking neural network can represent its input signals most accurately when excitatory and inhibitory currents are as strong and as tightly balanced as possible [47]. However, information transfer slides over the excitatory - inhibitory network with moderate energy input. Therefore the brain’s tightly regulated energy/information exchange with the environment forms a closed system.

(A) The CAP area decreases over time during high-frequency stimulation (HFS). The decay amplitude deviates from the absence of HFS, indicated by the dashed line (0.1 Hz, used for normalization to 1.0), and increase progressively with the increase in stimulation frequency (16 Hz, 50 Hz, 100 Hz). (B) Axonal ATP levels also decrease with increasing stimulation frequency, reaching a new steady state level which depends on the stimulation frequency [46].

Relationship to the carnot cycle

The Carnot cycle offers an upper limit on the efficiency that any classical thermodynamic engine can achieve during the conversion of heat into work. No engine operating between two heat reservoirs can be more efficient than the corresponding Carnot engine.

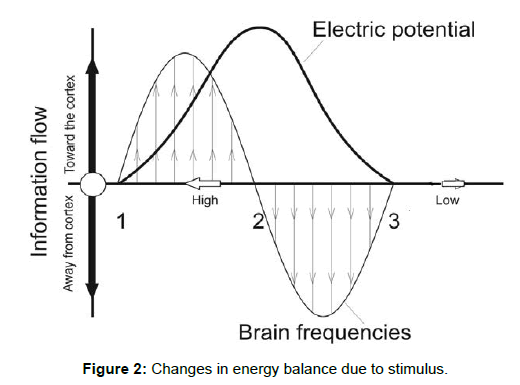
The Carnot cycle is an idealization, since no classical engine is reversible and physical processes involve some increase in entropy. Surprisingly, the Carnot bound can be surpassed in microscopic systems, because thermal fluctuations induce transient decreases of entropy, allowing for possible violations of the Carnot limit. Such a miniaturized Carnot engine was realized using a single Brownian particle [47,48]. The Carnot cycle represents execution of work in a heat bath. The process consists of two isothermal processes, where the working substance is respectively in contact with thermal baths at different temperatures Th and Tc, connected by two adiabatic processes, where the substance is isolated and heat is neither delivered, nor absorbed. In the brain, neural activation is forwarded via synaptic connections, allowing the analysis of energy/ information exchange based on the principle of least action. We suggest that the nervous entropic changes in information and resting state display a thermodynamic relationship with the Carnot cycle. The cortical insulation of the limbic system, which lies on the top of the resting state, correlates with the occurrence of evoked potential. In turn, the evoked potential triggers electric activities that restore the resting state (Figure 2). This recurrent energy /information exchange forms a closed system and allows the examination of brain activity based on thermodynamic considerations. Landauer’s principle shows how heat production is tied to information/energy transformations. The frequencies of the brain’s evoked cycle reflect both its computational limit and the added heat of stimulus, which also determines the energy usage via synaptic changes.

The brain frequencies change from high, on the left (1), to low, toward the right (3), determining the direction of information flow in the brain (shown by thin line). The resting state of the brain is energy neutral before stimulus (1) and after a response (3). Evoked potential are illustrated by 2. The high energy need of enhanced brain frequencies induces an urgency (indicated by 1), whereas the high amplitude of the lowest frequencies permits an overarching, global connective and mental vision, indicated by 3.

The brain’s energy/information cycle

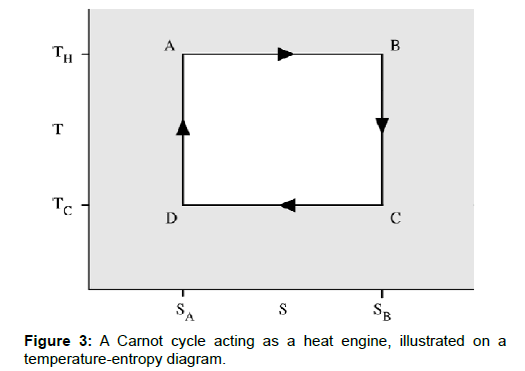
In the brain, stimuli increase frequencies, which correlate with heat absorbed by the system, giving rise to an increase in temperature (Figure 3). This phase, marked DA in the picture, correspond to the Carnot cycle’s adiabatic compression phase. In a classical gas, heat production is function of particles collisions, which is dependent on the temperature and the number of particles (volume of the gas). In neural networks as well as in deep learning systems, network connections correlate with collisions. Therefore, the number of dimensions corresponds to the volume of the gas, whereas the depth of the network might represent the temperature of the system. The second phase, marked by AB, in which the frequencies spread throughout the whole cortex, stands for the isothermal expansion (the signal expands, exerting work). The third, relaxation phase, marked by BC, stands in the brain for evoked potentials reversing the direction of the electric flow on lower frequencies; the reduction of temperature exerts work, by accumulating energy in the complexity of synaptic connections. In this phase, meanings and concepts emerge, based on the subjective information value of the stimulus. The fourth phase, marked by CD, correlates with the contraction phase of the cycle: the brain’s electric activities contract and recover the resting state.

The amount of thermal energy transferred in the process is the following:

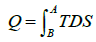
The area inside the cycle will then be the amount of work done by the system over the cycle.

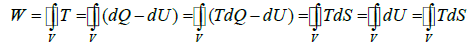
Since dU is an exact differential, its integral over any closed loop is zero: it follows that the area inside the loop on a T-S diagram is equal to the total work performed the amount of energy transferred as work is

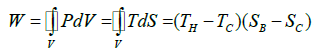The total amount of thermal energy transferred from the hot reservoir to the system will be

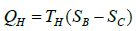
The efficiency η is defined to be:

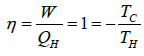
Where

1. W is the work done by the system (energy exiting the system as work)

2. QC is the heat taken from the system (heat energy leaving the system)

3. QH is the heat put into the system (heat energy entering the system) TC is the absolute temperature of the cold reservoir

4. TH is the absolute temperature of the hot reservoir

5. SB is the maximum system entropy

6. SA is the minimum system entropy

The heat absorbed by the system toward order increasing transformation: Therefore, the amount of released heat corresponds to the entropy decrease (in- creasing synaptic complexity) of the system. The cycle takes place between a hot reservoir at temperature TH and a cold reservoir at temperature TC. The vertical axis displays the temperature, whereas the horizontal axis the entropy. In the brain, during the (DA) compression phase, the stimulus increases the frequencies, due to heat absorbed by the system. In neural networks as well as in deep learning systems the depth and number of connections of the network is related to the system’s ability to produce work or to learning (AB): the frequencies spread throughout the whole cortex: the signal expands, exerting work. (BC): evoked potentials reverse the direction of the electric flow on lower frequencies (the temperature decreases, the energy leaves the system). CD: the electric activities contract and return to the resting state.

The brain’s energy/information cycle

Determines the temporal dimensionality of electric activities in understanding, comprehension and learning Landauer’s principle, originally developed for computation, was proven in increasingly sophisticated experiments and consequently, applicable for the tightly regulated environment of the brain [49-51]. According to the principle, information accumulation by electric activities of the brain during evoked states corresponds to enhanced temperature. Landauer’s principle also shows that the recovery of the resting state frees energy for work, due to information/energy transformation. This process correlates with lower temperature. Decreasing frequencies form a sink of low information content and increasing degrees of freedom [52]. Thus, evoked activities modify the temporal field curvature and dimensionality via bifurcations in the brain’s electric activities, whereas the resting, equilibrium state formulate Euclidean torus [32]. In contrast, decreasing frequencies increase the oscillations amplitude, thus activating greater brain regions, or modules [53]. Simultaneous activation of wider regions of the brain might engender mental coherence, ideas and learning. The potential assessment of neuronal activations and global cognitive processes in terms of brain energy cycle has immense potential in understanding various neural conditions, such as depression, PTSD and other neural disease.

Relationship between the resting state and learning

Sensory interaction increases between information content and entropy, but the living brain incessantly recovers its resting, low entropy state. Maintaining and restoring the resting state seems to be an inherent and essential part of healthy brain operation. Spontaneous brain activity, accounts for up to 70% of the great energy need of the brain [54]. Information input enhances frequencies and compresses time (by forming positive temporal curvature), which increases entropy, similar to a Brownian motion. In accordance with Landauer’s principle, heat must be released when the resting state is restored [55]. Surprisingly, deep learning can also be divided into phases that constitute similar entropic effects and energetic transformations, consisting of compression of information and relaxation, which culminates in representation of information [56,57]. This entropy conservation in closed systems is expressed by the low entropy principle [58].

Entropic considerations of the brain’s topology and activities: a mathematical treatment

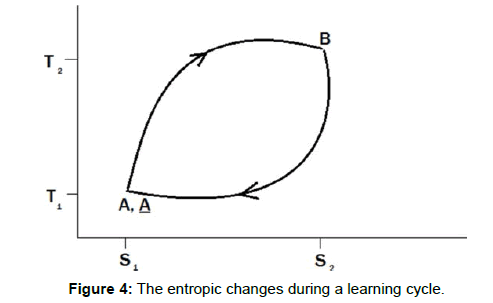
Brain activities might follow particle paths traversing surfaces of geometric spaces formed by temporal rhythms of electric activities [52]. Thus, electric activities might manifest as dimensional structures, that change from n- dimensional (e.g., a two-dimensional disk) to n+1 -dimensional structure (e.g., negative curvature surface, which correspond to temporal expansion) and n-1 dimensional surface (positive temporal curvature surface, which correspond to temporal compression). Since the energy cost of sensory processing is proportional to frequencies, sensory information is translated into an energy signal in the brain. The sensory transmission toward the sensory cortex via fast oscillations, and response via slow oscillations, form the polarity effects of the brain’s electromagnetic flows. Nevertheless, the strength and extent of synaptic connections (i.e. increasing synaptic complexity) differ before and after stimulus (Figure 4). The enhanced neural organization must be proportional with the release of thermal energy and consequent reduction of entropy. Therefore, stimulus, which increases temperature, might supply the energy to modulate synaptic strength or form new connections in the brain. The organizational constancy and charge neutrality of the resting state guarantees that the energy difference due to the released heat (as in a heat engine) leads to a higher order of the synaptic organization. Therefore, the brain is an active part of the environmental energy cycle.

A topological view of this synergy between the brain and the environmental energy cycles exhibits strong proximity both spatially and descriptively. The spatial strong proximity of the brain and environment is in the form of temporally overlapping cerebral energy and environmental energy readings (e.g., the occurrence energy highs and lows of the one set of readings overlaps with the occurrence similar readings of highs and lows in the other during the same timeframe) [59]. For example, let A and B represent nonempty sets of recordings of brain and environ- mental energy recordings that are temporally concomitant in situ. The spatial form of strong proximity is denoted by δ from the strong proximity axiom we have

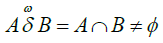
i.e., the two sets of energy readings overlap [60]. There is also a descriptively strong proximity between the two sets of energy readings. The descriptive form of strong proximity is denoted by 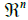. The subscript 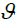refers to a mapping 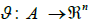on the set of readings A into an n-dimensional feature space 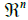, defined by 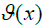(a feature vector in 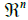) that is a feature value of a reading x ∈ A. Similarly, there is a mapping 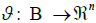on the readings in B into the feature space 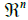. The two sets of energy readings with common descriptions give rise to a descriptive intersection (denoted by 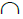) of the two sets:

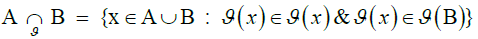
i.e., there is at least one cortical energy reading (e.g. cortical energy amplitude) in A that has the same description as an environmental energy reading (e.g. environmental energy amplitude) in B. From these structures, we can elicit a strong descriptive proximity between A and B in terms of

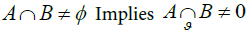
i.e., overlapping energy readings implies an overlap between the descriptions of the two sets of readings. This observation leads to the following descriptive proximity property:

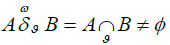
The importance of this pair of proximities lies in the fact it is then possible to derive Leader uniform topologies on pairs of sets of energy readings. This is done in the following manner. Start with a collection of sets of cerebral energy readings 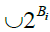and a collection of environmental energy readings 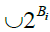gathered during within the same timeframe. For each given subset A 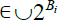, find all B .

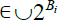Such that A 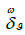B. Doing this for each given set of cerebral energy readings, leads to a collection of clusters of strongly near sets of readings. In effect, we have topologized the collections of energy readings by introducing a Leader uniform topology on the space of energy readings [61,62]. An important outcome of topologized energy readings is the introduction of a search space in which clusters of readings exhibit spatial and descriptive proximities. Moreover, our approach shows the role of observer in information processing: the history and current state of the brain is just as important in determining the degree of neuronal activation as the stimulus itself. Thus, the state of the observer i.e. the brain, determines the information value of the stimulus. This way, information processing in the brain is holographic. Thus, the degree of comprehension or understanding (manifested as increasing synaptic complexity) has a large subjective quality, the observer effect.

Conclusions

Physical principles often find application in other, seemingly unrelated fields, proving that the physical laws underline all of nature. The brain’s immense energy use engenders a readiness on which interaction with the environment is possible. Recent data of compound action potentials during high frequency stimulation have shown that strong electrical activity reduces the ATP content of the axon. This way, the brain’s electric activities depend on the temporary supply of energy sources, and thus the brain forms a closed system with respect to information processing. Here, in our investigation of brain processes, we analyzed the resting state in light of two important physical principles, the Carnot cycle and Landauer’s principle. We traced back the brain electromagnetic activities onto these principles based on the principle of least action.

(A) Sensory information activates the neural system by enhancing the frequency of oscillations, which corresponds to changes in temperature. The increase in frequencies leads to positive temporal curvature, which compresses time perception. The entropy also increases between S1 to S2 (B) the second part of the cycle recovers the low entropy state and the Euclidean geometry. The slowing frequencies correspond to negative temporal curvature and to increases in time perception, which slows down the system. (A) The entropy decrease leads to order, manifested as synaptic complexity, underpinning concepts and meaning. Therefore, the energy increase between A and A, is supplied by sensory stimulus. Or in other words, perception of stimulus modifies mental organization.

The brain’s fundamental regulation is founded on field effects of the resting state; in its constant interaction with the environment, the mind constantly changes and adapts. However, the maintenance of the resting state against the constant barrage of sensory activation by the environment contributes to the brain’s immense energy consumption. Sensory activation corresponds to information/entropy increase and the reduction of temporal dimensionality [32]. Landauer’s principle in the brain means that evoked activities correspond to enhanced ’temperature,’ whereas recovery of the resting state correlates with cooling down and the initial and final conditions differ in neural organization [55]. The incurred thermal energy might enhance neural organization, which engenders meaning, mental coherence and correlates with low entropy. Therefore, stimulus, which generates activation, might supply the energy to modulate synaptic strength or form new connections in the brain. Thus, Landauer’s principle might explain the relationship between the electric activities of the brain and the physiological states of the mind. Two sides of the brain energy/information cycle are bound by the organizational constancy and charge neutrality of the resting state. The brain, as well as deep learning systems maintains a permanent readiness state, on which energy/information cycle with the environment can take shape. Therefore, both in the brain and in deep learning systems, Maxwell’s demon can reverse the second law of thermodynamics. The existence of the stable resting state turns the brain into a globally static system. In this way, the brain’s self-regulation utilizes the information input delivered by the environment, leading to an increase of its neural organization (mental capacity, corresponding to greater synaptic complexity). In a highly interconnected relationship, the brain is part of the thermodynamic cycle of the environment it modifies its environment, but it is evolved and changed by interaction. A connection between life processes and the entropic changes of the environment was suggested by Schrodinger 1945 and was further developed by Déli [58]. We have shown that the constant barrage of information by the environment induces a thermodynamic cycle in the brain, similar to the Carnot cycle, which increases synaptic organization and complexity, i.e. order. The ability to transform information into energy seems to be the most essential quality of the brain. However, the brain is compelled by comprehension and interpretation of visual, auditory, tactile experience or taste by the stimulus. The brain neither engages nor controls the environment. Instead, the environment highjacks the brain to gather and process incoming information [41,58]. Furthermore, the environment extracts energy from the brain for sensory information: the environment provokes and extorts the brain’s energy consumption needs. Feeding on complex organic compounds reduces the environment’s entropy. Thus, evolution of life is part the environment’s entropy management. The brain’s immense energy use during its resting state ensures that very tiny changes in potential can trigger considerable activation and order increasing transformations. Thereby, thinking, memory and other conscious processes require minute computational costs. This permits us to uncover how energy/information transformations in the brain satisfy physical principles.

References

1. Shulman RG, Rothman DL, Hyder F (2009) Baseline brain energy supports the state of consciousness. Proc. Natl. Acad. Sci. USA 106: 11096-11101.
2. Dehghani N, Peyrache A, Telenczuk B, Le Van Quyen M, Halgren E (2016) Dynamic Balance of Excitation and Inhibition in Human and Monkey Neocortex Sci Rep 6: 23176.
3. Okun M, Lampl I (2009) Balance of excitation and inhibition.Scholarpedia 4:7467.
4. Gerd G, Dittrich P, Klaus-Peter Z (2011) Artificial wet neuronal networks from compartmentalised excitable chemical media. ERCIM NEWS 85: 30-32.
5. Kim JK, Fiorillo CD (2017) Theory of optimal balance predicts and explains the amplitude and decay time of synaptic inhibition Nature Communications 8: 14566.
6. Vladimir VK, Epstein IR (2011) Excitatory and inhibitory coupling in a one- dimensional array of Belousov-Zhabotinsky micro-oscillators: Theory. Physical Review E 84: 066209.
7. Luczak A, McNaughton BL, Harris KD (2015) Packet-based communication in the cortex. Nat. Rev. Neurosci 16: 745-755.
8. Duncan TL, Semura JS (2004) The Deep Physics Behind the Second Law: Infor- mation and Energy As Independent Forms of Bookkeeping. Entropy 6: 21-29.
9. Martin JS, Smith NA, Francis CD (2013) Removing the entropy from the definition of en- tropy: clarifying the relationship between evolution, entropy, and the second law of thermody- namic.cs. Evol. Educ. Outreach 6: 30.
10. Del Rio L, Berg EAJ, Renner R, Dahlsten O, Vedral V (2011) The thermodynamic meaning of negative entropy. Nature 474: 61-63
11. Haji-Akbari A, Engel M, Keys AS, Zheng X, Rolfe G, et al. (2009) Disordered, quasicrystalline and crystalline phases of densely packed tetrahedra Nature 462: 773-777.
12. Haji-Akbari, A, M Engel, SC Glotzer (2011) Phase Diagram of Hard Tetrahedra Journal of Chemical Physics 135: 194-101.
13. Yamada Y, Kawabe T (2011) Emotion colors time perception unconsciously. Con- sciousness and Cognition. Elsevier Inc 20: 1-7.
14. Landauer R (1961) Irreversibility and heat generation in the computing process. IBM J Res Dev 5: 183-191.
15. Doiron B, Litwin-Kumar A, Rosenbaum R, Ocker GK, Josi AK (2016) The mechanics of state-dependent neural correlations. Nat. Neurosci 19: 383-393.
16. Wright NC, Hoseini MS, Wessel R (2016) Adaptation modulates correlated subthreshold re- sponse variability in visual cortex. J. Neurophysiol 118: 1257-1269.
17. Gazzaniga MS (2009) The Cognitive Neurosciences. (4th edtn). MIT Press. Cambridge, Massachusetts, United States.
18. Kavalali ET, Chung C, Khvotchev M, Leitzet J, Nosyreva E, et al. (2011) Spontaneous neurotransmission: an inde- pendent pathway for neuronal signaling? Physiology (Bethesda) 40: 45-53.
19. Donnell OC, Van Rossum MC (2014) Systematic analysis of the contributions of stochastic voltage gated channels to neuronal noise. Front. Comput. Neurosci 8: 105.
20. Jensen O, Gips B, Bergmann TO, Bonnefond M (2014) Temporal coding organized by cou- pled alpha and gamma oscillations prioritize visual processing. Trends Neuroscipii 37: 357-369.
21. Friston K (2010) The free-energy principle: a unified brain theory? Nat Rev Neurosci 11: 127-138.
22. Sporns O (2013) Network attributes for segregation and integration in the human brain. CurrOpinNeurobiol 23: 162-171.
23. Tozzi A (2015) Information Processing in the CNS: A Supramolecular Chemistry? Cognitive Neurodynamics 9: 463-477.
24. Koch C, Massimini M, Boly M, Tononi G (2016) Neural correlates of consciousness: progress and problems. Nat Rev Neurosci. Apr 9: 307-21.
25. Touboul J (2012) Mean-field equations for stochastic firing-rate neural fields with de- lays: Derivation and noise-induced transitions. Physica D: Nonlinear Phenomena 241: 1223-1244.
26. Guterstam A, Abdulkarim Z, Ehrsson HH (2015) Illusory ownership of an invisible body reduces autonomic and subjective social anxiety responses. Scientific Reports 5: 9831
27. Mancini F, Longo MR, Kammers MPM, Haggard P (2011) Visual distortion of body size modulates pain perception. Psychological Science APS 22: 325-330.
28. Bell PT1, Shine JM (2015) Estimating Large-Scale Network Convergence in the Human Functional Connectome. Brain Connect 5: 565-74.
29. Northoff G, Qin P, Nakao T (2010) Rest-stimulus interaction in the brain: a review. Trends Neurosci 33: 277-284.
30. Fingelkurts AA, Fingelkurts AA, Neves CFH (2009) Phenomenological architecture of a mind and operational architectonics of the brain: the unified metastable continuum. New Math Nat Comput 5: 221-244.
31. Atasoy S, Pearson J, Donnelly I (2016) Human brain networks function in connectome-specific harmonic waves. Nat. Commun: 7.
32. Tozzi A, Peters JF (2016a) Towards a Fourth Spatial Dimension of Brain Activity. Cognitive Neurodynamics 10: 189-199.
33. Tozzi A, Peters JF (2016b) A Topological Approach Unveils System Invariances and Broken Symmetries in the Brain. Journal of Neuroscience Research 94: 351-65.
34. Tozzi A (2016) Borsuk-Ulam Theorem Extended to Hyperbolic Spaces. In: Computational Proximity. Excursions in the Topology of Digital Images169-171.
35. Robinson PA, Zhao X, Aquino KM, Griffiths JD, Sarkar S et al. (2016) Eigenmodes of brain activity: Neural field theory predictions and comparison with experiment. Neuroimage 142: 79-98.
36. Teki S (2016) A Citation-Based Analysis and Review of Significant Papers on Timing and Time Perception. Frontiers in Neuroscience 10: 330.
37. Soares S, Atallah BV, Paton JJ (2016) Midbrain dopamine neurons control judgment of time. Science 354: 1273-1277.
38. Jo HG, Wittmann M, Hinterberger T, Schmidt S (2014) The readiness potential reflects intentional binding. Front. Hum. Neurosci 8: 421.
39. Kranick SM, Hallett M (2013) Neurology of volition. Exp. Brain Res 229: 313-327.
40. Stanghellini G, Ballerini M, Presenza S, Mancini M, Northoff G, et al. (2016) Abnormal Time Experiences in Major Depression: An Empirical Qualitative Study. Psychopathology 50: 125-140.
41. Déli E (2015) The Science of Consciousness. Self-published.
42. Fingelkurts AA, Fingelkurts AA (2014) Present moment, past, and future: mental kaleido- scope. Front. Psychol 5: 395.
43. Sengupta B, Tozzi A, Coray GK, Douglas PK, Friston KJ (2016) Towards a Neuronal Gauge Theory. PLOS Biology 14: e1002400.
44. Collell G, Fauquet J (2015) Brain activity and cognition: a connection from thermodynamics and information theory. Frontiers in Psychology 6: 818.
45. Engl E Attwell D (2015) Non-signalling energy use in the brain. J Physiol 593: 3417-3429.
46. Trevisiol (2017) eLife 2017. 6: e24241.
47. Koren V, Denave S (2017) Computational Account of Spontaneous Activity as a Signature of Predictive Coding. PLoS Computational Biology 13: e1005355.
48. Martinez IA, Roldan E, Dinis L, Petrov D, Parrondo JMR, et al. (2016) Brownian Carnot engine 12: 67–70.
49. Bérut A (2012) Experimental verification of Landauerâs principle linking information and thermodynamics. Nature (London) 483: 187-190.
50. Jeongmin H, Brian L, Scott D, Jeffrey B (2016) Experimental test of Landauer’s principle in single-bit operations on nanomagnetic memory bits. Science Advances 2: e1501492.
51. Landauer R (1961) Irreversibility and heat generation in the computing process. IBM J Res Dev 5: 183 - 191.
52. Tozzi A, Peters JF (2017) Critique of pure free energy principle. Physics of Life Reviews.
53. Silva E, Crager K, Puce A (2016) On dissociating the neural time course of the processing of positive emotions. Neuropsychologia 83: 123-137.
54. Tomasi D, Wang GJ, Volkow ND (2013) Energetic cost of brain functional connectivity. PNAS 110: 13642-13647.
55. Pop-Jordanova N, Pop-Jordanov J (2005) Spectrum-weighted EEG frequency ("brain-rate") as a quantitative indicator of mental arousal. Prilozi 26: 35-42.
56. Shwartz-Ziv R, Tishby N (2017) Opening the black box of deep neural networks via information.
57. Gao X, Duan LM (2017) Efficient representation of quantum many-body states with deep neural networks. Nat Commun 8: 662.
58. Déli E (2017) Evaluation of Machâs Principle in a Universe with four spatial dimensions.
59. Peters JF (2016) Computational Proximity. Excursions in the Topology of Digital Images. Edited by Intelligent Systems Reference Library, Springer-Verlag, Berlin.
60. Peters JF (2016) Proximal physical geometry. Advances in Mathematics: Scientific Journal 5: 241-268.
61. Leader S (1959) On completion of proximity spaces by local clusters, Fundamenta Mathematicae 48: 201-216.
62. Peters JF (2015) Proximal Voronoi regions, convex polygons, Leader uniform topology, Advances in Mathematics 4: 1-5.