Research Article, Geoinfor Geostat An Overview Vol: 6 Issue: 1

Applicability of Geostatistical Method to Ground Investigation for Embankments of Narrow Detached Houses

Shinya Inazumi^1*, Ken-Ichi Shishido² and Kohei Urakami³

¹Department of Civil Engineering, Shibaura Institute of Technology, Toyosu Koto, Tokyo, Japan

²Tomec Corporation, Shibadaimon, Minato, Tokyo, Japan

³Department of Social Informatics, Kyoto University, Gokasho, Uji, Kyoto,Japan

*Corresponding Author : Shinya Inazumi
Associate Professor, Department of Civil Engineering, Shibaura Institute of Technology, Toyosu Koto, Tokyo, Japan
Tel: +81358598360
E-mail: inazumi@shibaura-it.ac.jp

Received: October 27, 2017 Accepted: February 13, 2018 Published: February 21, 2018

Citation: Inazumi S, Shishido K, Urakami K (2018) Applicability of Geostatistical Method to Ground Investigation for Embankments of Narrow Detached Houses. Geoinfor Geostat: An Overview 6:1. doi: 10.4172/2327-4581.1000174

Abstract

Keywords: Detached houses ground; Geostatistics; Ground characteristic; Ground investigation; Improved Swedish weight sounding test; Kriging method

Introduction

Ground subsidence and liquefaction have often been observed on detached house grounds. For example, during the great East Japan earthquake on March 11, 2011, large-scale ground liquefaction was observed widely in Urayasu City, Chiba Prefecture, Japan. These phenomena involved the permanent ground displacement on a large scale, damaging public infrastructures extensively. However, appropriate investigation methods and countermeasures are still under development and have not been established yet, partly because the suitable study areas are very confined [1].

In addition, in-situ subsurface investigations of the subsoil properties are performed only at the limited points due to temporal, economic, and physical constraints. Not limited to detached-house grounds, this is also the case with relatively large-scale constructions such as tunnels [2]. Therefore, with respect to unknown points or areas, it is common to predict the ground characteristics, including its physical properties, using some method based on a finite number of subsurface measurements. Nevertheless, accurate estimates of the grounds characteristics at specific areas and points are necessary for the establishment of a subsurface investigation and liquefaction countermeasures system [3].

In the ground survey, it is thought that it is essential to obtain a lot of investigation results in a limited place in order to detail the inside of the ground. Therefore, it is necessary to establish a testing machine capable of measuring results at finer intervals. Moreover, in the interpolation of the conventional ground survey results, a method of linearly interpolating between the drilled stationary points is main stream, and it is common that the information in the ground is roughly grasped. Therefore, even in interpolation of ground survey results, development and establishment of methods for predicting unknown points or unknown regions in the ground with high precision based on the ground survey results are considered to be indispensable tasks. It is best to establish measures to deal with ground problems after making the ground more detailed.

In this study, we conduct a detailed ground survey for the ground using an improved Swedish weight sounding test (Nippon screw weight system; hereinafter referred to as NSWS test (machine)) on a soft ground in a certain detached house embankment ground. Then, using the measured converted N value data as an example, using the Geostatistical method which was originally not used in the narrow detached house ground, the converted N value is not known unknown in the ground prediction of planar spatial distribution of points / unknown regions is carried out. The Geostatistical method is a method of giving a mathematically optimal weight by setting a predicted value at an unknown point in a space as a weighted average of known values. Although this method was used for estimating the strength of homogeneous ground, there are few cases used in heterogeneous and narrow ground like detached house embankment ground. Therefore, there is still unknown part in heterogeneous ground for the Geostatistical method. In this study, we will verify the effectiveness of the new ground survey tester and develop it as a new application case study of the Geostatistical method by applying the Geostatistical method to the heterogeneous ground.

Current State of Subsurface Investigations and Prediction of Cross-Sectional Distributions

Current state of subsurface investigations

Multiple methods exist for subsurface investigation. However, two of these are most commonly used: the standard penetration test (hereinafter, referred to as the SPT test) and the Swedish sounding test (hereinafter, referred to as SWS test). The SPT test is a test for determining ground hardness, tightness, and the geological structure; it is conducted during sampling, by penetrating the SPT sampler dynamically [4]. The SPT test is frequently performed during construction of lifelines such as roads, dams, and large-scale buildings. On the other hand, in the SWS test, the lot equipped with a screw point, whose edge is drill-shaped, is loaded with weight and penetrates the ground; we measure the rotation frequency required to penetrate up to 0.25 m of ground depth [4]. Based on the required weight load and the rotational frequency, we calculate the converted N-value. When detached houses are built, the SWS test is used to investigate the targeted ground. Both tests allow N-values and converted N-values to be measured (calculated) only in relatively wide intervals. For example, the SPT test measures N-values every 0.3 m, and the SWS test measures converted N-values at 0.25 m depth intervals. In other words, although it is possible to measure the ground physical property (the N-value distribution) using either method, with a certain level of accuracy, it is impossible to measure changes in the detailed N-value distribution in the ground. Moreover, the SWS test used for detachedhouse grounds is considered completed, when the examiner judges that drilling has reached the rigid layer [4]. Consequently, even if the rigid layer is only comprised of pebbles, the test may be finished. For these reasons, it is impossible to measure the detailed N-values and the converted N-values at present. Furthermore, due to temporal, economic, and physical reasons, in-situ soil investigation cannot be performed in finite locations. Therefore, it is difficult to grasp the physical property value of all the target ground only by the ground survey and it is a situation where the ground cannot be investigated in detail.

Current state of predictions of cross-sectional distribution

It is difficult to understand the physical properties of all the objects’ ground areas only by subsurface investigation. Therefore, in most cases, the properties are predicted empirically, based on a finite number of measured values. In other words, experts evaluate the results of investigation, and the so-called “drawing” is carried out, or the values are predicted by applying to each sample the weight in inverse proportion to the distance or the square distance as the weighted average [5]. However, in the former case, the expert opinion affects the estimation, and it takes a huge amount of time. In the latter, certain problems remain, including ambiguity in the mathematical justification for each weighting. In these methods, as the reliability of the assessments cannot be quantified, the entire ground area cannot be understood. Thus, it is thought that it will be easier to grasp the detailed information in the ground by using a method that is relatively time-consuming and accurate.

Prediction of Cross-Sectional Distribution for Ground Characteristics by Geostatistics

Geostatistics is a discipline with a relatively short history. In the early 1960s, for the first time, Georges Matheron, a mathematician at Mines Paris Tech, defined “Geostatistics” as the prediction method of cross-sectional distribution and presented its concept. In this study, based on converted N-values obtained through the NSWS test, we predict the cross-sectional distribution using the Kriging Geostatistical method [6].

Overview of the kriging method

The Kriging method is the most fundamental technique in Geostatistics, commonly used in meteorology and forestry, which was proposed by D.G. Krige, an engineer in South Africa [6]. This method is also used in agriculture, climatology, fisheries sciences, and other fields. In civil engineering, this method is used in hydraulic engineering and geotechnical engineering [7]. The Kriging method allows the cross-sectional fluctuating distribution of a physical property to be predicted objectively [8]. There are several established variations of this method, such as the ordinary Kriging method, the simple Kriging method, and the indicator Kriging method [9].

In this study, we use the ordinary Kriging method, which includes weighting limitations, and allows for the relative representation of a space-random field.

Ordinary Kriging method

When the investigated physical property assumes different values based on the probability distribution, it is considered a random variable [10]. If the expected value is constant throughout the target area, and the covariance depends only on the distance between the data and is irrelevant of the data location, stationary is achieved [11]. Geostatistics is based on the assumption that these random variables exhibit stationary [12]. The method of calculating the weighted average of variables under the stationary conditions is the ordinary Kriging method.

The estimated value 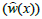at a certain point (x) is given generally as the weighted average of the measured values (w(x )(i 1, 2,...,n)) at n points (x_i) around (x), from Eq. 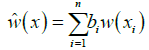(1).

(1)

When the difference between the estimated value from Eq. (1) and the true value 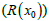is the estimated error (R(x₀)) and the expected value is obtained from Eq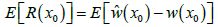. (2)

(2)

Where, if the abovementioned stationarity is assumed for a stochastic process (w), the expected value of the estimated error (R(x₀)) becomes zerp, and the impartiality term of the estimated value shown in Eq. (3) is derived.

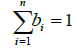(3)

Also, when the minimum value is calculated from the estimated error distribution shown in Eq. (4), using the Lagrange multipliers method, Eq. (5) can be obtained.

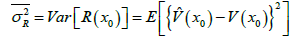(4)

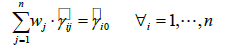(5)

where 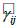is called the “variogram” and is the value that reflects the cross-sectional distribution of a physical property (Eq. (6)), which depends on the covariance function 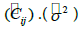is the dispersion of the stochastic process (V).

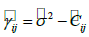(6)

In addition, the dispersion of (V) in the estimated error of Eq. (6) is converted to Eq. 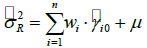(7).

(7)

If Eqs. (3) and (5) are solved together, the weighting (w_i) and the Lagrange undetermined multiplier (μ)are obtained, and, by substituting them into Eqs. (1) and (7), the estimated value 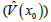and the dispersion of (V) in the estimated error 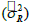at the random location (x0) can be obtained.

Semi-variogram

The cross-sectional distribution of physical properties can be expressed using several methods, such as the covariance function, the correlation function, and the variogram. Here, we use the semivariogram, a type of variogram that has the advantage of easy function modeling, even if the distribution of the physical property is infinitely large [2].

The semi-variogram is represented as half the mean square of the difference in the physical property value between two locations, as shown in Eq. 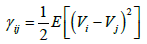(8).

(8)

where V_i and V_j refer to the physical property located at points i and j, respectively. In addition, the used semi-variogram is a discrete function; it is impossible to measure a theoretical semi-variogram (γ_ij) that is a continuous function, from the obtained data. Thus, as shown in Eq. (9), the semi-variogram is obtained by discretizing the data in couples of any distance. This is referred to as the experimental variogram (γ * (h)).

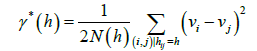(9)

Where v_i and v_j are the values for distances h_ij and N (h) In addition, when the experimental variogram for any distance (h) is obtained, the allowable distance ±Δh is provided, and γ * (h) is calculated from the average value of the discrete values within the range.

In order to obtain this semi-variogram using the Kriging method, it is necessary to approximate the discretized data based on a functional model [13]. In this study, a Gaussian type semi-variogram is used, which is simple and strict when the ground is modeled as a random field, particularly in the three dimensions [14]. The Gaussian type semi-variogram is shown in Eq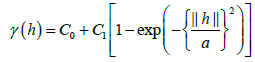. (10)

(10)

where a is called the “range,” and its value indicates that the distance between the data cannot be correlated, if a exceeds this range. C₀ is called the “nugget”, and it reflects the data uncertainty, including the measurement error; if this value is too large, the prediction accuracy decreases considerably. (C₀ + C₁) is called the “sill”, the convergence value at which the semi-variogram becomes constant, when the distance between data exceeds it. The range, the nugget, and the sill are obtained from the results of Eq. (9), using the least-square method [15].

Searching over an ellipsoidal region

In predicting the cross-sectional distribution, only the data included in searching over an ellipsoidal region is used. Searching over an ellipsoidal region refers to a spheroid with a certain diameter, which is determined from the range obtained from semi-variogram [13]. In this study, the depth data for two points is frequently treated. If the Kriging method does not make a prediction considering the data configuration, the accuracy may be poor [16]. Therefore, in this study, we search over an ellipsoidal region considering the range and data configuration, to perform the prediction of the cross-sectional distribution.

Overview of the NSWS test

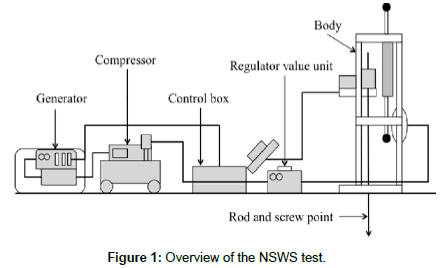
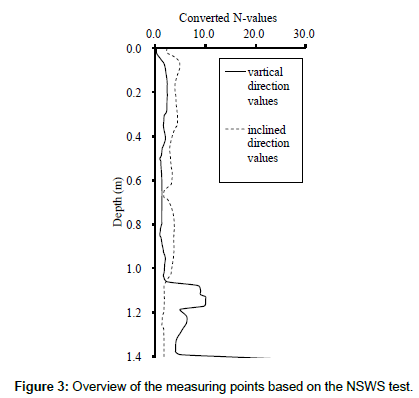
The NSWS test is a reformed version of the conventional SWS test, in which the ground soundness is evaluated from the weight of the penetration rod and the rotation [1]. Figure 1 shows an overview of the NSWS test. The “inclination direction measurement” is one of the features of the NSWS test. Inclination direction measurement refers to measuring ground characteristics including physical properties by penetrating the rod diagonally into the ground in Figure 2. Figure 3 shows an example of the converted N value in the vertical direction and the converted N value in the inclination direction actually measured by the NSWS test.

Site Summary of In-situ ground investigation by the NSWS test

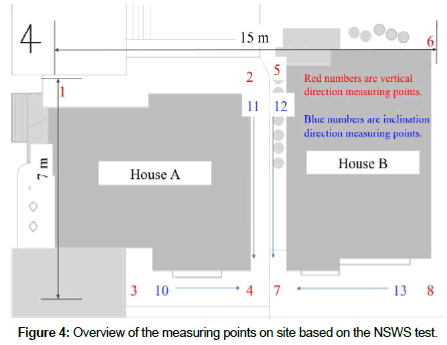
The study site is a bank of detached houses constructed in Nishinomiya City, Hyogo Prefecture. The site is a stepwise residential land in the slope with two lines of general two-story detached houses. In part of the premises, ground subsidence was generated, partially deforming the buildings and the surrounding concrete walls. The measuring points are the vertical measuring points on the north side of the premises (1, 2, 5, and 6), and the vertical measuring points on the south side of the premises (retaining wall side) (3, 4, 7, and 8), as shown in Figure 4. Moreover, inclination direction measurement was carried out at points 10, 11, 12, and 13.

Plan and Results for Prediction of Cross-Sectional Distribution by Geostatistical Methods

The ground characteristics from the predicted cross-sectional distribution in this study are converted N-values obtained from the NSWS test. Using these converted N-values as a case study, we examine the applicability of the Kriging interpolation method to detached-house grounds. In the NSWS test, the converted N-value is measured at 0.01 m depth intervals. Thus, based on the converted N-values obtained by the NSWS test, the Kriging method is applied to predict the cross-sectional distribution in the depth direction using the converted N-values. In order to obtain highly accurate predictions, it is necessary to acquire measurements at regular depth intervals. In addition, for comparison, we predict the cross-sectional distribution from 0.25 m measurements using the SWS test, in the same manner.

Prediction of cross-sectional distribution for the cross section between measuring points 1 and 5

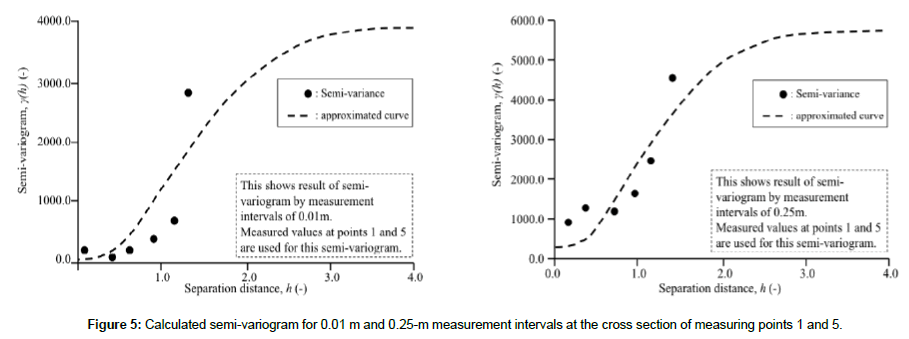
When the Kriging method is used, modeling is performed by approximating the semi-variogram. Semi-variogram at 0.01 m measurement interval and semi-variogram at 0.25 m measurement interval are shown. The results of each semi-variogram are shown in Figure 5. The figure on the left is a semi-variogram at the 0.01m measurement interval, the figure on the right is the semi-variogram at the measurement interval of 0.25 m. respectively. In semi-variogram at 0.01 m measurement interval, C₀ =1.0, C₀+C₁=3112.0, and a=3.06. In semi-variogram at 0.25 m measurement interval, C₀=320.0, C₀+C₁=5750, and a=2.62. In general, the prediction accuracy increases when C₀ decreases, whereas correlation is improved for larger values of a. Comparing both results, it appears that C₀ is smaller, a is larger, and the measurement accuracy is higher for the 0.01 m interval measurements than for the 0.25 m interval measurements, and the converted N-value is correlated better.

Both results differ significantly, regarding the number of measured values to be considered. The number of raw measured values is the same; however, when the number of measured values extracted from the raw data is different, this difference falls within the prediction accuracy boundaries. Thus, accuracy improves when the number of measured values is large, allowing for the prediction of the crosssectional distribution. Therefore, the cross-sectional distribution should be predicted taking into account as many measured values for the vertical direction as possible. Therefore, it is necessary to predict the spatial distribution after measuring a lot of data in the vertical direction as much as possible for spatial distribution prediction in order to make the inside of the ground more detailed.

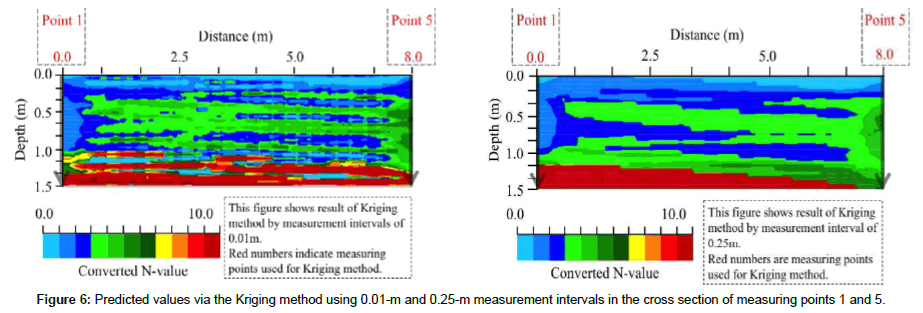
The predicted values by the Kriging method for the measurement intervals of 0.01 m and 0.25 m are shown in Figure 6, respectively. The figure on the left is the result of kriging at 0.01 m measurement interval, the figure on the right is the result of kriging at 0.25 m measurement interval. In both cases, the soft ground, where the converted N-values are below 5, from the surface layer down to almost 1.0 m depth, is frequently predicted. The converted N-values are predicted accurately (Figure 6). In addition, we do not observe any significant difference between the results shown in these two figures. Therefore, prediction of the cross-sectional distribution for 0.25 m measurement intervals is considered accurate. This is attributed largely to the difference in the nature of the semi-variogram, as well as to the number of measured values used. Based on the discussion presented in the previous section, it is thought that, due to the nature of the semi-variogram, the accuracy of the predicted cross-sectional distribution using 0.01 m measurement interval values is higher than that using 0.25 m measurement interval values.

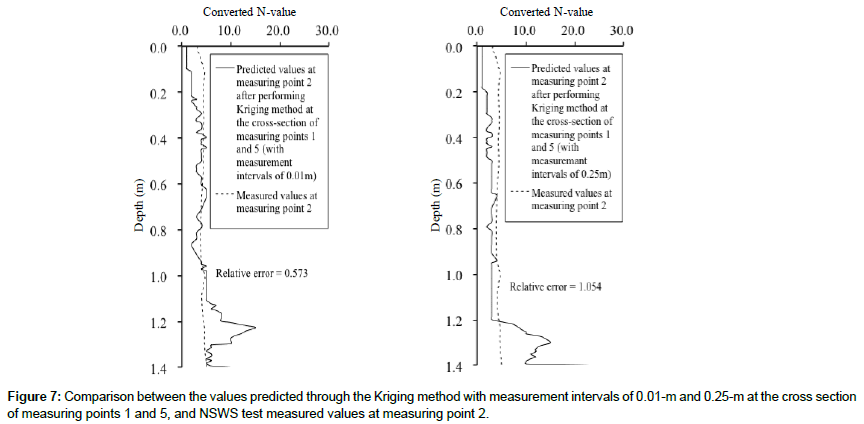
Measuring point 2 is located 7 m away from measuring point 1, almost along the line connecting measuring points 1 and 5 (Figure 4). Therefore, it is considered that the converted N-value in the vertical direction of measuring point 2 can be compared with the predicted values of the cross-sectional distribution for the cross section between measuring points 1 and 5. Based on the predicted values of the crosssectional distribution using 0.01 m and 0.25 m measurement interval values at measuring points 1 and 5, we compare these predicted values (converted N-values predicted with the Kriging method) with the measured values (converted N-values obtained through the NSWS test) in the vertical direction at measuring point 2 (Figure 7). The figure on the left compares the predicted value with the measured value at the 0.01 m measurement interval, and the figure on the right compares the predicted value and measured value at the 0.25 m measurement interval. From these figures, predicted values close to the measured values are obtained at less than 1.2 m depth in both cases. However, the predicted values are different from the measured values (converted N-values obtained by the NSWS test) at depths greater than 1.2 m in both Figure 7. For a quantitative evaluation, the relative errors between the predicted values and the measured values are approximated. The relative error is 0.523 for measurement intervals of 0.01 m, and 1.054 for measurement intervals of 0.25 m. From this, the error is smaller when the Kriging method is applied with measurement intervals of 0.01 m, and it is possible to make higher accuracy predictions, when C₀ in the semi-variogram is smaller. Therefore, it is considered preferable to take into account the number of the measured values, when predicting the cross-sectional distribution of the ground characteristics.

Comparison of the prediction methods

The distribution of ground characteristics has been predicted by the “drawing method,” which is a conventional method, using N-values and converted N-values obtained through the SPT test and the SWS test.

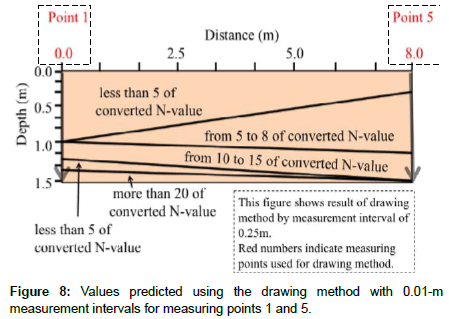
Based on the measured values obtained with the NSWS test at measuring points 1 and 5, the prediction of the cross-sectional distribution with the Kriging method (Figure 6) and the drawing method (Figure 8) are compared. The surface portion is considered the soft layer with a converted N-value of 5 or less (Figures 6 and 8). The difference is that, at the points around measuring point 5, the ground with a converted N-value of 5 or more is abundantly predicted from the place with relatively shallow depth in Figure 8, compared with Figure 6. Large converted N-values are not predicted until the depth increases (Figure 6). From this, it is clear that interpolation differs significantly between the Kriging method and the drawing method.

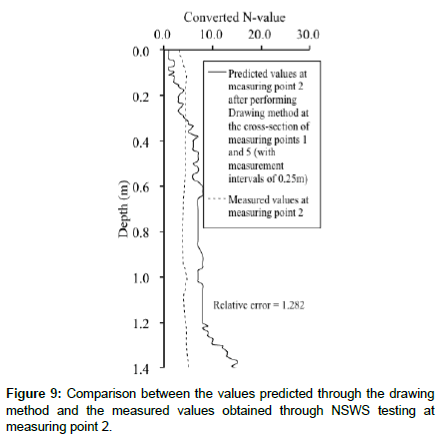
The values predicted using the drawing method is also compared with the measured values. Figure 9 shows the measured values (converted N-values obtained with the NSWS test) and the predicted values (converted N-values predicted with the drawing method). The results start to differ significantly around the depth of 1.3 m (Figure 9). Therefore, it is difficult to predict the cross-sectional distribution with relatively high accuracy using the drawing method. In addition, the relative error in the separation level between the measured values and the predicted values is 1.282. Comparing this with the cross-sectional distribution predicted with the Kriging method with measurement intervals of 0.01 m and 0.25 m, the largest relative error occurs using the drawing method. Consequently, in both cases, the cross-sectional distribution can be predicted with higher accuracy through the Kriging method than with the drawing method.

Predictions of cross-sectional distribution for different cross-sections of the measuring points

Measuring points 1, 2, 5, and 6 are located almost on a straight line (Figure 4). In the previous section, prediction of cross-sectional distribution was made only at measuring points 1 and 5, and the obtained values (converted N-values obtained through the NSWS test) were compared to the predicted values at measuring point 2. In this section, the cross-sectional distribution is predicted at measuring points 1, 5, and 6, and the converted N-values at measuring point 2 are predicted and compared with the measured values. Thus, we determine the difference between the predicted values and the measured values at measuring point 6, and the difference in the estimation accuracy when the predicted values increase in the horizontal direction.

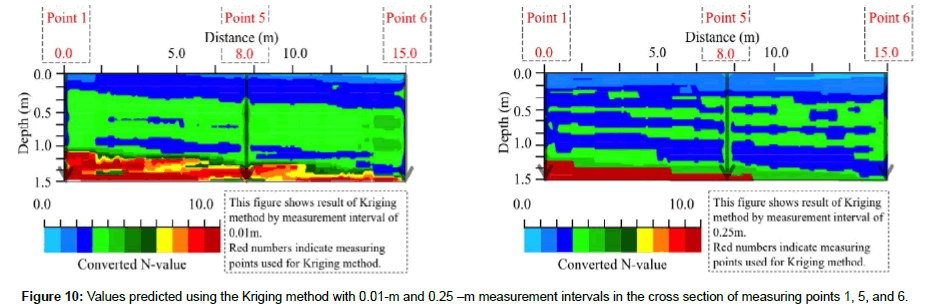
Figure 10 shows the predicted values based on the Kriging method at the cross section of measuring points 1, 5, and 6. The figure on the left is the result of kriging at 0.01 m measurement interval, the figure on the right is the result of kriging at 0.25 m measurement interval. In Figure 10, the characteristics of the soft ground are predicted along the vertical direction (depth) by adding the corresponding measured values at measuring point 6. Thus, the predicted values of the cross-sectional distribution are changed by taking into account the measured values at different measuring points.

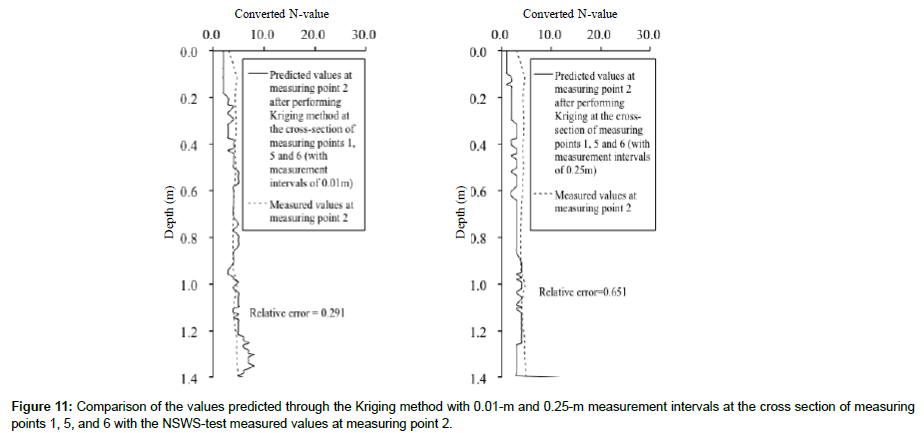
Figure 11 shows the comparison between the measured and the predicted values at measuring point 2. The figure on the left compares the predicted value with the measured value at the 0.01 m measurement interval, and the figure on the right compares the predicted value and measured value at the 0.25 m measurement interval. When the measurement interval of 0.01 m is applied, the two values differ below 1.5 m depth (Figure 11). However, when the measurement interval of 0.25 m is used, a large separation occurs around the depth of 1.4 m. Comparing the respective predicted cross-sectional distributions (Figures 6 and 10), large converted N-values do not appear in depth due to the addition of measuring point 6. Moreover, comparing Figures 7 and 11, the values around 1.4 m depth are similarly separated by the addition of measuring point 6, even though the overall accuracy is higher. In addition, the relative errors in both cases are small, 1.0 or less. Comparing this with the results at measuring point’s 1 and 5 (Figure 6), both relative errors are smaller. Therefore, the predicted converted N-values in the vertical direction at measuring point 2 become more accurate by taking into account the measured values at measuring point 6, and it is thought that the predicted values around measuring point 2 are affected by the measured values at measuring point 6. Moreover, by increasing the number of data to be considered, prediction accuracy is increased, and it is clear that the prediction accuracy of the Kriging method increases by increasing the number of measurement points in the horizontal direction and measuring a lot of data. Therefore, it is necessary to measure as much data as possible in the vertical and horizontal direction.

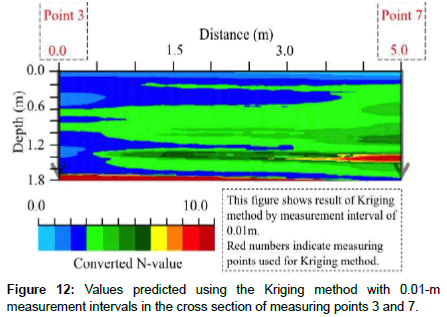
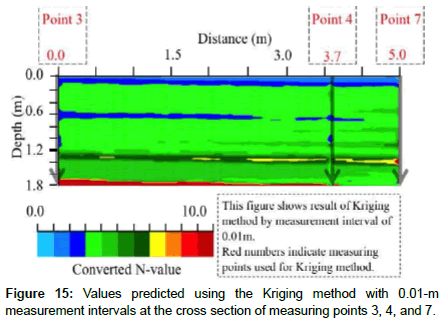
Measuring points 3, 4, and 7 are located almost on a straight line (Figure 4). Thus, the cross-sectional distribution is predicted on the cross section of measuring points 3 and 7 to check the difference between the measured values and those predicted values at measuring point 4. The results using the Kriging method at the same cross section are shown in Figure 12. The ground is soft down to the relatively deep part (Figure 12). Moreover, a ground layer with high converted N-values is predicted around the depth of 1.8 m. This is attributed to the converted N-values of the debris close to measuring point 3.

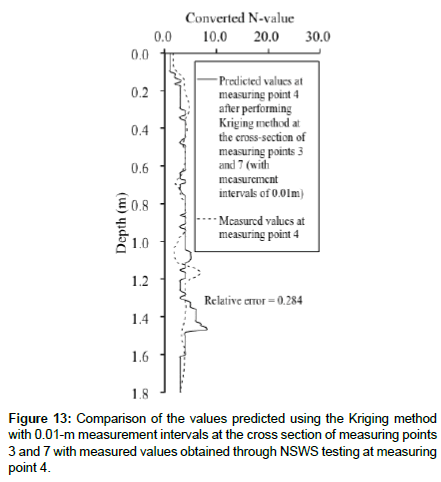
Figure 13 shows the comparison of the measured values and those predicted. The separation from the measured values is smaller down to the depth (Figure 13). In addition, the overall relative error is calculated, which turned out to be 0.284. Thus, the value of the relative error is 1.0 or less, close to 0, showing that the error is relatively small. Therefore, the Kriging method is considered applicable for predicting the cross-sectional distribution of ground characteristics including physical properties at narrow detached house embankment grounds.

Predictions of cross-sectional distribution considering measured values in the inclination direction

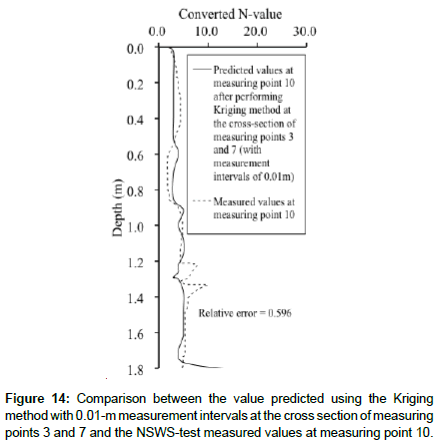
The converted N-values may also be measured in the inclination direction through NSWS testing. Based on this, by comparing the measured values with predicted values in the inclination direction, it is possible to check whether the Kriging method can predict the crosssectional distribution successfully. Figure 14 shows the measured converted N-values from the NSWS test at measuring point 10 in the inclination direction toward measuring points 3 and 4. Therefore, since the predicted values (converted N-values predicted with the Kriging method) at measuring point 10 are determined by predicting the cross-sectional distribution from the values at measuring points 3 and 7 (Figure 12), it is possible to compare the measured values with the predicted values.

Figure 14 shows the comparison of the measured values and those predicted at measuring point 10 based on Figure 12. The separation from the measured values is small down to about 1.7 m depth (Figure 14). However, the separation from the measured values is larger beyond the depth of about 1.8 m. This is because the place brought to close at the measuring point 3 has an influence. The overall relative error is 0.596, less than 1.0, and thus relatively small. Therefore, the Kriging method can be used to predict the cross-sectional distribution successfully.

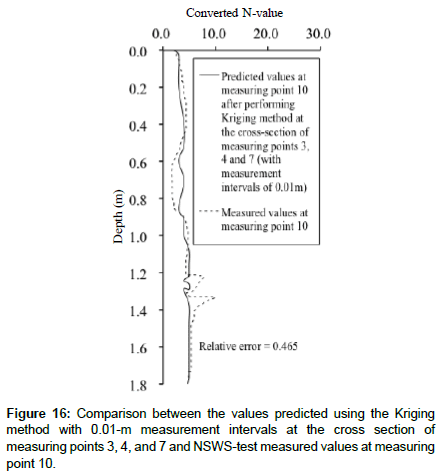
In order to predict the converted N-values in the inclination direction, the cross-sectional distribution is predicted based on the measured values only at measuring points 3 and 7 (Figure 12). Here, we investigate the effect of interpolation on the predicted values, by adding the converted N-values measured in the inclination direction at measuring point 4.

Figure 15 presents the predicted cross-sectional distribution based on the measured values at measuring points 3, 4, and 7, which is used to predict the converted N-values in the inclination direction. Compared with the predicted cross-sectional distribution using the measured values at measuring points 3 and 7 (Figure 12), we confirm that the size of the weak surface layer changes. However, the other distributions are not significantly changed, and weak layers appear across the deeper ground layers. Figure 16 shows the comparison of the measured values (converted N-values obtained with the NSWS test) with the predicted values (converted N-values predicted with the Kriging method) at measuring point 10 based on Figure 15. The difference is small down to about 1.7 m in depth (Figure 16). However, it increases below 1.8 m, probably due to the presence of debris near measuring point 3. In addition, the overall relative error is 0.465, i.e., less than 1.0, which is considered small. Therefore, it is considered that the kriging method is effective also when predicting the property value in the inclination direction.

In all the above results, the cross-sectional distribution is predicted based on the converted N-values only in the vertical direction. Therefore, next, we examine the differences in the predicted crosssectional distribution based on the measured values in the inclination direction.

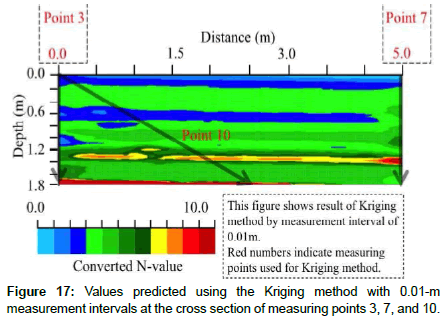
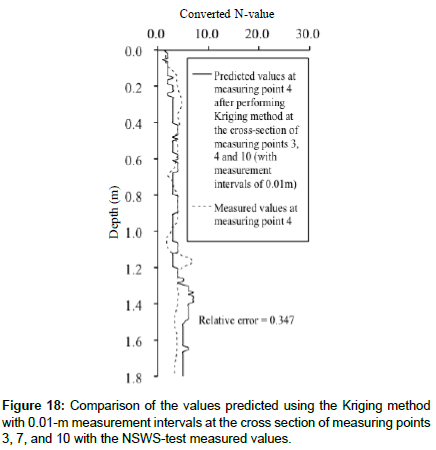
The measuring point 10 shows the converted N-values measured in the inclination direction toward the measuring points 3 and 4. Thus, we examine the interpolation effect on the predicted crosssectional distribution at measuring point 3, 7, and 10. Figure 17 shows the predicted cross-sectional distribution at measuring points 3, 7, and 10. Comparing Figures 12 and 17 the predicted values around 1.5 m depth near measuring point 7 are only slightly different. Moreover, the values at measuring point 4 are also predicted from this cross section, and they are compared here with the measured values.

Figure 18 shows the comparison between the measured values (converted N-values obtained with the NSWS test) and the predicted values (converted N-values predicted with the Kriging method) at measuring point 4 based on Figure 4. The difference from the measured values is small at all depths (Figure 18). In addition, the overall relative error is 0.347, i.e., less than 1.0, which is considered small. However, compared with the results of Figure 13, the predicted values using the measured values at only measuring points 3 and 7 are lower, although the difference is very small. Consequently, the measured values in the inclination direction may be ignored when predicting the cross-sectional distribution. Therefore, we consider that the measured values in the inclination direction should only be used as ancillary results.

Effectiveness of New Ground Survey Tester and New Application Example of Kriging Method

In this research, spatial distribution prediction by the Kriging method was performed using both the survey results at 0.01 m intervals at which the data measurement interval can be measured with NSWS and the survey results at 0.25 m intervals that can be measured with SWS. From the results, it was confirmed that the error in the survey results at intervals of 0.01 m, which is the measurement interval of NSWS, is smaller in any case in comparison between the measured value and the predicted value. Comparing the results of both spatial distribution predictions, it was confirmed that the 0.01 m interval, which is the measurement interval of NSWS, can interpolate the distribution of ground physical property values in detail. From these results, it is thought that by precisely measuring ground physical property values, we can predict the interior of the ground in detail and at the same time with high precision. Therefore, the effectiveness of NSWS which is a new ground survey tester is considered to be very high.

Next, in various cases, the Kriging method was carried out to summarize the state of the distribution of the ground physical property values and the relative error with the actual measurement value, and at the same time, it compared with the prediction result of the spatial distribution by the conventional wire drawing. From these results, it was confirmed that the Kriging method can predict the ground physical property value with high accuracy even in heterogeneous ground. In addition, it can be confirmed that the Kriging method predicts the physical property value in detail also in the state of distribution, and from this it is considered that information in the ground can be grasped in detail, not in a rough but detailed manner, by using the Kriging method. From this, it is considered that the Kriging method can be applied sufficiently in heterogeneous ground. Inhomogeneous ground will have larger variability in comparison with homogeneous ground. Therefore, it is considered that using the Kriging method is more suitable for predicting the ground physical property value of heterogeneous ground because it can predict fine physical values.

In the Great East Japan Earthquake, large-scale ground problems occurred (for example, liquefaction) in detached house embankment ground. One of the reasons for this was considered to be due to the fact that the state of the ground just under the house was only grasped roughly and detailed information was not known. In order to solve such problems from now on, it is essential to grasp the state of the ground in more detail, and to solve the ground problems beforehand on that basis, as mentioned in the first chapter.

The NSWS used in this study can be thought from the result of this research that it is a testing machine that is necessary to solve the ground problem because it can measure the ground physical property value finely. Moreover, it is considered that the application in heterogeneous ground by the Kriging method is sufficiently applicable from the result of this research. Therefore, in order to solve the ground problems in the future, it is essential to establish so that both the testing machine used this time and the Kriging method will be applied to the heterogeneous ground. And it is thought that we can solve and elucidate the ground problem by widely notifying even in the homogeneous ground.

Conclusion

In this study, spatial distribution prediction is performed using Geostatistical method based on data of ground physical property values measured using soft and thin, heterogeneous embankment ground (detached house ground) using NSWS test (machine) prediction of surface strength of target ground was carried out. Based on the results of surface strength prediction, we investigated the effectiveness of a new survey tester and applied case analysis of the Kriging method in heterogeneous ground. As these results, the following conclusion was obtained.

(1) In this study, Kriging method was carried out for both the 0.01 m interval which is the measurable interval of the ground physical property value of NSWS and the 0.25 m interval which is the measurable interval of the ground physical property value of SWS. As a result, it was confirmed that the error interval from the surveyable interval of NSWS, 0.01 m interval is smaller than the measured value as a result of spatial distribution prediction, and the distribution of the ground physical property value can be grasped in detail. Therefore, NSWS is considered to be a very effective testing machine in order to grasp the state of the ground well.

(2) Kriging is performed in various cases on a heterogeneous ground. As a result, it was confirmed that the error from the measured value was small in any case. Therefore, it is considered that Kriging method can be sufficiently applied even in heterogeneous ground.

(3) From the results of spatial distribution prediction based on the difference in the number of measurement points, it can be confirmed that the deviation from the measured value decreases as the number of measurement points increases in the horizontal direction in the survey. From this, it is considered that as the number of data in the horizontal direction increases, the prediction accuracy increases, so it is necessary to measure as much data as possible in the horizontal direction. Therefore, NSWS is considered to be highly effective because it can measure ground physical property values in the horizontal direction.

In this study, the ground characteristics, including the physical properties of the target ground, are revealed through cross-sectional interpolation. At the same time, the applicability of the Kriging method to narrow grounds such as detached-house grounds is investigated by comparing the predicted with the measured values. In the future, the target ground is going to be evaluated from the viewpoint of risk engineering, discussing the difference with the measured values.

References

1. Nishimura G, Inazumi S, Okita K (2016) The investigation and reinforcement for residential grounds located on inclined bedrocks. Journal of the Society of Materials Science 65: 74-79.
2. Yoshida M, Miyajima M and Kitaura M (1999) Estimation of spatial liquefaction potential and its application to evaluation of liquefied ground flow at plane ground. Journal of the Japan Society of Civil Engineers 49: 155-166.
3. Noguchi T, Tanaka M, Watanabe Y, Sakagami S, Sadamura T (2011) Verification of 3-D visualization of ground at Tokyo International Airport. Japanese Geotechnical Journal 6: 69-79.
4. Fujii M, Satoru K, Futaki M, Tamura M, Ijuin H et al. (1996) Relation between NSW of Swedish weight sounding and N-value of standard penetration test. AIJ Journal of Technology and Design 3: 64-68.
5. Ohnishi Y, Tanaka M, Ohsawa H (1992) Basic study on estimation of physical parameters in heterogeneous ground. Doboku Gakkai Ronbunshu. 457: 51-58.
6. Georges M (1963) Principles of geostatistics. Economic Geology 58: 1246-1266.
7. Matsui K, Maeda Y, Isii K, Suzuki M (1991) Probabilistic estimation of spatially distributed N-values and its application to pile design. Doboku Gakkai Ronbunshu 436: 57-64.
8. Koike K, Liu C, Tamura A (2005) Application of spatio-temporal geostatistics to detection of secular changes of environments in a closed sea. Geoinformatics 16: 3-15.
9. Miyaya Y, Kogure K, Honjo Y (1997) Estimation of spatial variation of soil profiles in a submarine clayey deposit. Japan Society of Civil Engineers 13: 441-446.
10. Kobayashi A, Hinata H, Fujii K (1998) Back Analaysis of Hydraulic Conductivity Distribution with Geostatistical Simulation Results as Prior Information. Journal of applied mechanics 1: 129-136
11. Syoji T, Koike K (2007) Kriging-estimation of spatial data taking account of error. Journal of the Geothermal Research Society of Japan 29: 183-194.
12. Cao R, Zee MY, Gomez E (2014) Geostatistical applications in petroleum reservoir modelling. Journal of the Southern African Institute of Mining and Metallurgy 114: 625-631.
13. Stein ML. Interpolation of spatial data: some theory for kriging. Springer Science & Business Media; 2012 Dec 6.
14. Honjo Y, Otake Y, Kato H (2012) A simplified scheme to evaluate spatial variability and statistical estimation error of local average of geotechnical parameters in reliability analysis. Journal of Japan Society of Civil Engineers 68: 41-55
15. Journel AG, Huijbregts CJ (1978) Mining Geostatistics, Blackburn Press, New Jersey, USA.
16. Araki SS, Ueda T, Yamamoto S, Tohno S (2011) A study of the prediction method of the spatial distribution of ozone by Kriging in Otsu city and its surrounding area. Journal of Japan Society for Atmospheric Environment 46: 241-250.