Research Article, Res Rep Math Vol: 2 Issue: 1
Extending the Applicability of an Ulm-Newton-like Method under Generalized Conditions in Banach Space
Ioannis K. Argyros1* and Santhosh George2
Department of Forestry and Biodiversity, Tripura University, Suryamaninagar, Agartala, India
*Corresponding Author : Ioannis K. Argyros Department of Mathematical Sciences, Cameron University, Lawton, OK 73505, USA, E-mail: iargyros@cameron.edu
Received: November 02, 2017 Accepted: January 15, 2018 Published: February 10, 2018
Citation: Argyros IK, George S (2018) Extending the Applicability of an Ulm-Newton-like Method under Generalized Conditions in Banach Space. Res Rep Math 2:1
Abstract
The aim of this paper is to extend the applicability of an Ulm-Newtonlike method for approximating a solution of a nonlinear equation in a Ba-nach space setting. The su cient local convergence conditions are weaker than in earlier works leading to a larger radius of convergence and more precise error estimates on the distances involved. Numerical examples are also provided in this study. AMS Subject Classi cation: 65H10, 65G99, 65J15,49M15.
Keywords: Ulm’s method; Banach space; local / semi-local conver-gence
Introduction
In this study we are concerned with the problem of approximating a locally unique solution x of equation
F (x) = 0; (1.1)
where, F is a Frechet{di erentiable operator de ned on a convex subset of a Banach space B1 with values in a Banach space B2.
A large number of problems in applied mathematics and also in engineering are solved by nding the solutions of certain equations. For example, dynamic systems are mathematically modeled by di erence or di erential equations, and their solutions usually represent the states of the systems. For the sake of sim-plicity, assume that a time{invariant system is driven by the equation x = R(x), for some suitable operator R, where x is the state. Then the equilibrium states are determined by solving equation (1.1). Similar equations are used in the case of discrete systems. The unknowns of engineering equations can be func-tions (di erence, di erential, and integral equations), vectors (systems of linear or nonlinear algebraic equations), or real or complex numbers (single algebraic equations with single unknowns). Except in special cases, the most commonly used solution methods are iterative{when starting from one or several initial approximations a sequence is constructed that converges to a solution of the equation. Iteration methods are also applied for solving optimization problems. In such cases, the iteration sequences converge to an optimal solution of the problem at hand. Since all of these methods have the same recursive structure, they can be introduced and discussed in a general framework [1-12].
Moser [13] proposed the following Ulm’s-like method for generating a sequence fxng approximating x :
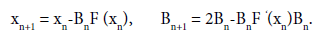
Method (1.2) is useful when the derivative F 0(xn) is not continuously invertible (as in the case of small divisors [1-8,10,11,13-15]). Moser studied the semi-localpconvergence of method (1.2) and showed that the order of convergence is 1 + 2 if F 0(x?) 2 L(B2; B1p). However, the order of convergence is faster than the Secant method (i.e. 2). The quadratic convergence can be obtained if one uses Ulm’s method [14,15]
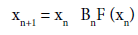
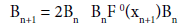
The semi-local convergence of method (1.3) has also been studied in [1-9]. As far as we know the local convergence analysis of methods (1.2) and (1.3) has not been given. In the present paper, we study the local convergence of the Ulm’s-like method de ned for each n = 0; ; 2; 3; : : : by
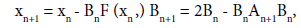
where An is an approximation of F’(xn). Notice that method (1.4) is inverse free, the computation of F0(xn) is not required and the method produces suc-cessive approximations {Bn} ≈ F’(x*)-1
In Section 2, we present the local convergence analysis of the method (1.4) and in Section 3, we present the numerical examples.
Local convergence analysis
The local convergence analysis of the method (1.4) is given in this section. Denote by U (v, ζ) the open and closed balls in B1, respectively, with center v ∈ B1 and of radius ζ>0.
Let w0 : [0,+ ∞] → [0,+ ∞] and w : [0,+ ∞] →[0,+ ∞] be continuous and nondecreasing functions satisfying w0 (0)= w(0)=0.
Let also q ∈ [0,1] be a parameter. Define functions Õ and ψ on the interval [0,+ ∞] by
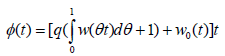
and
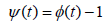
We have that ψ (0) = −1 and for sufficiently large 0 0 t ≥ t,ψ (t ) > 0 . By the intermediate value theorem equation ψ (t) = 0 has solutions in the interval (0, t0). Denote by the smallest such solution. Then, for each t ∈[0,ρ ]we have
0 ≤ψ (t) < 1. (2.1)
We need to show an auxiliary perturbation result for method (1.4).
LEMMA 2.1 Let 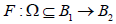 be a continuously Frechet-differentiable operator. Suppose that there exist
be a continuously Frechet-differentiable operator. Suppose that there exist 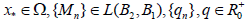 , continuous and nondecreasing functions
, continuous and nondecreasing functions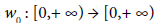 and
and 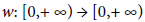 such that for each x∈Ω,n = 0,1,2,.. and θ ∈[0,1]
such that for each x∈Ω,n = 0,1,2,.. and θ ∈[0,1]
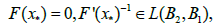
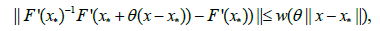
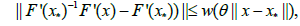
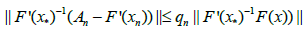 that for each
that for each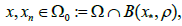
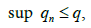
where 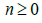
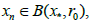
and 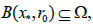
where 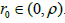
Then, the following items hold
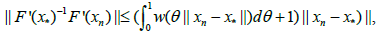
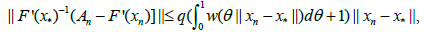
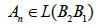
And
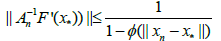
Proof we shall first show estimate (2.11) holds. Using (2.1), we have the identity
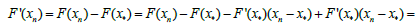
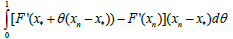 (2.14)
(2.14)
Then, by (2.4) and (2.14) we have that
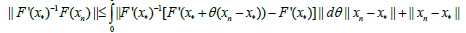
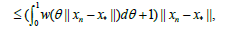
which shows (2.10). Moreover, by (2.5), (2.6) and (2.10) we obtain that
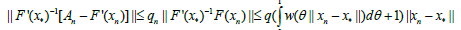
which shows the estimate (2.11). Furthermore, using (2.3), (2.4), (2.10), (2.11) and the definition of r0 we get that
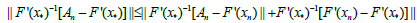 (2.15)
(2.15)
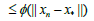
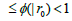
It follows from (2.15) and the Banach lemma on invertible operators [1,4,6,11] that (2.12) and (2.13) hold.
REMARK 2.2 In earlier studies the Lipschitz condition [1-15]
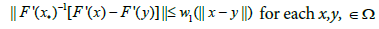 (2.16)
(2.16)
is used which is stronger than our conditions (2.3) and (2.4). Notice also that since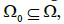
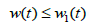 (2.17)
(2.17)
and
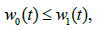 (2.18)
(2.18)
where functions w1 is as function w but defined on Ω instead of Ω0.The ratio 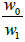 can be arbitrarily large [1,4,6]. Moreover, if (2.16) is used instead of (2.3) and (2.4) in the proof of Lemma 2.1, then the conclusions hold provided that r0 is replaced by r1 which is the smallest positive solution of equation
can be arbitrarily large [1,4,6]. Moreover, if (2.16) is used instead of (2.3) and (2.4) in the proof of Lemma 2.1, then the conclusions hold provided that r0 is replaced by r1 which is the smallest positive solution of equation
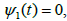 (2.19)
(2.19)
where 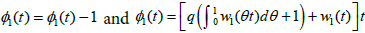 it follows from (2.10), (2.17), (2.18), (2.19) that
it follows from (2.10), (2.17), (2.18), (2.19) that
Furthermore, strict inequality holds in (2.20), if (2.17) or (2.18) hold as strict
Inequalities. Finally, estimates (2.11) and (2.12) are tighter than the corresponding ones (using (2.16)) given by
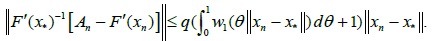
Let λ be a parameter satisfying be a continuous and no decreasing function.
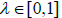
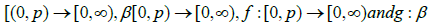
Moreover, define functions
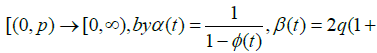
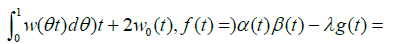
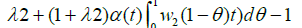
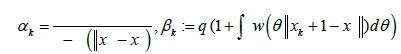
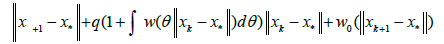
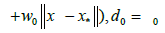
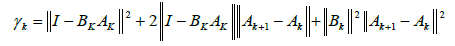
Parameters 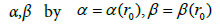 and quadratic equatio
and quadratic equatio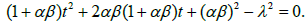 Then, we have
Then, we have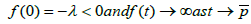
Denote byρ0 the smallest solution of equation f(t)=0 in (0,p) tthen, we have
that for each 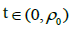
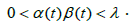
In view of the above inequality the preceding quadratic equation has a unique positive solution denoted by ρ+ and a negative solution. Define parameter γ by
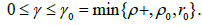
Then, we have that
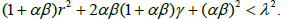
Notice that we also have that 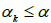 and
and 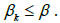
Next, we present the local convergence of method (1.4).
THEOREM 2.3 Under the hypotheses of Lemma 2.1 and with r0 given in (2.9) for λ ∈[0,1) further suppose there exists function 2 0 w :[0,r )→[0,+∞) continuous and no decreasing such that for each 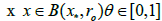 and
and
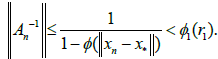
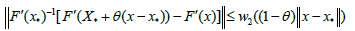 for each
for each 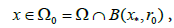
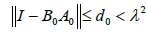 and
and
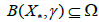
where γ is given in (2.22). Then, sequence  generated by the method (1.4) for
generated by the method (1.4) for 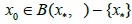 is well defined , remains in * B(x ,γ ) and converges to x*
is well defined , remains in * B(x ,γ ) and converges to x*
Proof. We have by hypothesis (2.25) that 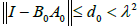 so
so
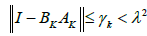
is true for k = 0: Suppose that (2.27) is true for all integers smaller or equal to k: Using Lemma 2.1, we have the estimate
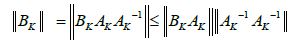
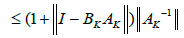
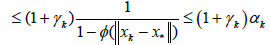
In view of method (1.4) for n = k; we can write in turn that
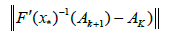
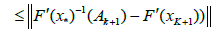
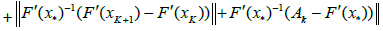
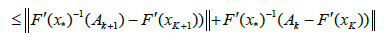
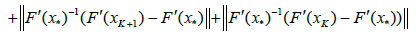
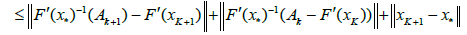
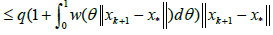
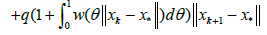
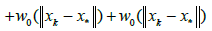
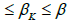
By the definition of method (1.4), we have the estimate
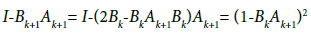
Then, by (2.32), (2.29) for n = k; we get in turn that
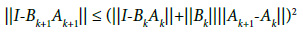
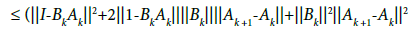
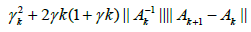
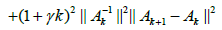
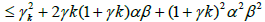

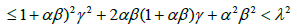
which shows (2.27) for n = k +1: Then, using the induction hypotheses, (2.24), and the definition of γ
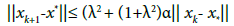
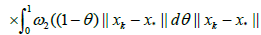
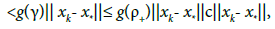
where c = g[0,1], so 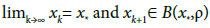
REMARK 2.4 (a) As noted in Remark 2.2 conditions (2.4) and (2.5) can be replaced by (2.24).
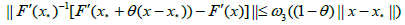 (2.36)
(2.36)
for each x∈Ω and θ ∈[0,1], where function ω3is as ω1:
We have that ω1 (t)≤ ω3 (t). Then, in view of Remark 2.2 and (2.24) the radii of convergence as well as the error bounds are improved under the new approach, since old approaches use only (2.36) with the exception of our approach in [2,5].
The results obtained here can be used for operators F satisfying autonomous differential equations [1,4,6,11] of the form
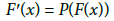
Where 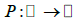 is a continuous operator. Then, since F′(x*)= P(F(x*))= P(0), we can apply the results without actually knowing x* For example, let F(x) =ex-1. Then, we can choose P(x) = x + 1
is a continuous operator. Then, since F′(x*)= P(F(x*))= P(0), we can apply the results without actually knowing x* For example, let F(x) =ex-1. Then, we can choose P(x) = x + 1
(c) The local results obtained here can be used for projection methods such as the Arnoldi’s method, the generalized minimum residual method (GM-RES), the generalized conjugate method (GCR) for combined Newton/finite projection methods and in connection to the mesh independence principle can be used to develop the cheapest and most efficient mesh refinement strategies [1,4,6].
(d) Let L0, L, L1, L2, L3 be positive constants. Researchers, choose ω0(t)= L0t, ω(t)= Lt, ω1(t)= L1t, ω2(t)= L2t, and ω3(t)= L3t, Moreover, if we choose Ω0=Ω and L=L1 then, our results reduce to the ones given by where the second order of convergence was shown with the Lipschitz conditions given in non-affine invariant form. In Example 3.1, we shall show that the radii are extended and the upper bounds on ||xn- x*|| are tighter if we use ω0, ω, ω2 instead of using ω0 and ω we used in [5] or only ω3 as used in [2,7-15].
Numerical examples
Example 3.1 let 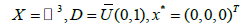 Define function F on D for ω=(x,y,z)T by
Define function F on D for ω=(x,y,z)T by
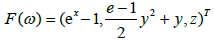
Then, the Frechet-derivative is defined by
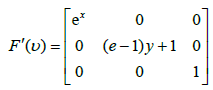
Notice that using the Lipschitz conditions, we get 
 and
and 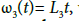 where
where 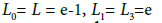 and
and 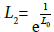 Moreover, choose
Moreover, choose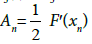 to obtain
to obtain 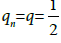
The parameters are 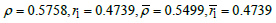
where the bar answers corresponding to the case when only ω3 is used in the derivation of the radii.
Example 3.2 Let
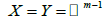 for natural integer
for natural integer
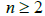 X and Y are equipped with the max-norm
X and Y are equipped with the max-norm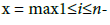
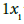 The corresponding matrix norm is
The corresponding matrix norm is
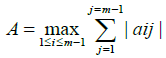
For 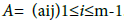 On the interval [0; 1], we consider the following two point boundary value problem
On the interval [0; 1], we consider the following two point boundary value problem
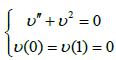 (3.1)
(3.1)
[6,8,9,11]. To discretize the above equation, we divide the interval [0; 1] into m equal parts with length of each part: h=1/m and coordinate of each point: xi=I h with i=0,1,2,…,m. A second-order finite difference discretization of equation (3.1) results in the following set of nonlinear equations
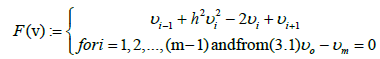 (3.2)
(3.2)
Where 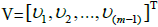 For the above system-of-nonlinearequations, we provide the Frechet derivative
For the above system-of-nonlinearequations, we provide the Frechet derivative
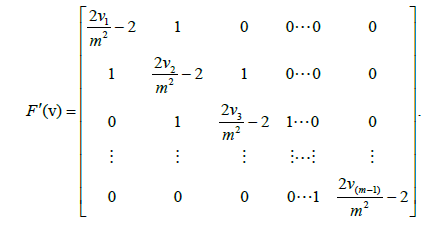
We see that for
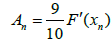
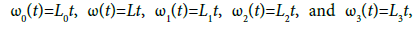 where
where 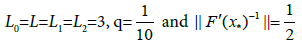 The parameters are
The parameters are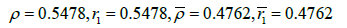
where the bar answers corresponding to the case when only ω3 is used in the derivation of the radii.
References
- Argyros IK (2007) Computational Theory of Iterative methods. Elsevier Publ. Comp. New York.
- Argyros IK (2009) On Ulm's method for Frechet differentiable operators.J Appl Math Computing 31: 97 - 111.
- Argyros IK (2009) On Ulm's method using divided differences of order one. Numer. Algorithms 52: 295-230.
- Argyros IK, Hilout S (2014) Computational Methods in Nonlinear Analysis - Efficient Algorithms, Fixed Point Theory and Applications, World Scientific.
- Argyros IK (2014) On an Ulm's -like method under weak convergence conditions in Banach space. Advances in Nonlinear Variational Inequalities 2: 1-12.
- Argyros IK, Magrenan AA (2017) Iterative methods and their dynamics with applications, CRC Press, New York.
- Burmeister W (1972) Inversionsfreie Verfahren zur L•osung nichtlinearer Opera-torgleichungen, ZAMM 52: 101-110.
- Ezquerro JA, Hernandez MA (2008) The Ulm method under mild differentiability conditions, Numer. Math. 109: 193-207.
- Gutierrez JM, Hernandez MA, Romero N (2008) A note on a modi cation of Moser's method, Journal of Complexity, 24: 185-197
- Hald OH (1975) On a Newton-Moser-type method, Numer. Math. 23: 411-426.
- Kantorovich LV, Akilov GP (1982) Functional Analysis, Pergamon Press, Ox-ford Publications, Oxford.
- Moret I (1987) On a general iterative scheme for Newton-type methods, Numer Funct Anal Optim 9: 1115-1137.
- Moser J (1973) Stable and random motions in dynamical systems with special emphasis on celestial mechanics. Herman Weil lectures, Annals of Mathe-matics Studies, Princeton University Press, Princeton, NJ.
- Ulm S, Das Majorantenprinzip und die Sehnenmethode (Russ.), Izv Akad Nauk Est SSR 13: 217-227.
- S. Ulm (1967) Uber Iterationsverfahren mit suksessiver Approximation des in-versen Operators (Russ.), Izv Akad Nauk Est SSR 16: 403-411.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi 