Research Article, Geoinfor Geostat An Overview Vol: 6 Issue: 1
Filtration of Components of Sieroszowice Mine Copper Ore Deposit Variogram Models by Means of Estimation Ordinary Kriging Technique
Barbara Namysłowska-Wilczyńska*
Wroclaw University of Science and Technology, Wrocław, Poland
*Corresponding Author : Barbara Namysłowska-Wilczyńska
Professor, Wroclaw University of Science and Technology, Wrocław, Poland
Tel: +48600035216
E-mail: Barbara.Namyslowska-Wilczynska@pwr.edu.pl
Received: December 12, 2017 Accepted: January 05, 2018 Published: January 12, 2018
Citation: Namysłowska-Wilczyńska B (2018) Filtration of Components of Sieroszowice Mine Copper Ore Deposit Variogram Models by Means of Estimation Ordinary Kriging Technique. Geoinfor Geostat: An Overview 6:1. doi: 10.4172/2327-4581.1000175
Abstract
This paper presents the results of investigations into the spatial variation of the basic geological parameters of strategic mineral resources, i.e. the copper ore deposits in the Foresudetic Monocline in the Lubin-Sieroszowice area (SW part of Poland).
The studies were based on data obtained by sampling the deposit with groove samples distributed mostly uniformly (at a spacing of 15÷20 m) over the area of Sieroszowice mine post-mining block S-1. The studies concerned the Cu grade in and the thickness of the (recoverable) deposit concentrated in Weissliegend sandstones, Zechstein copper-bearing shales, calcareous-dolomitic formations and moreover the accumulation (quantity) of the deposit.
An evaluation of the basic statistics, an analysis of the distribution histograms and an examination of the correlation r between the values of the deposit parameters are presented against the geological structure of the copper ore deposit in block S-1. Isotropic and relative semivariograms of the deposit parameters were calculated. The shapes of the isotropic semivariograms were approximated using composite theoretical (geostatistical) models consisting of a cubic model and a spherical model, combined with the nugget effect.
Estimated averages Z* and estimation standard deviation σk for the investigated deposit parameters in the centres of the elementary grid blocks were estimated taking into account the determined parameter values of the theoretical isotropic semivariogram models.
An attempt was undertaken to successively filter off the individual components, making up the composite semivariogram models of the copper ore deposit parameters, using the ordinary (block) kriging technique. Nugget effect C0 and the cubic model, the spherical model and the sum of the cubic model and the spherical model were filtered off.
As a result of the estimations a very detailed picture of the variation in the values of the basic deposit parameters within block S-1 was obtained, which was then presented on various raster maps of the surface distributions of averages Z* (together with the corresponding values of estimation standard deviation σk). The maps show the mineralization of the deposit rocks with copper compounds, broken down into the particular components corresponding to the adopted models and to nugget effect C0.
Thanks to the filtering the mutual shares of the different model components in overall variation C of the considered parameters were identified and the scale and extent of both short- and longterm variation were assessed.
Zones of elevated or reduced copper concentrations and subareas varying in the width of the mineralized lithological profile of the deposit series, i.e. in the thickness of the mineralized deposit rocks, and also of various accumulations (quantity) were identified within block S-1.
Keywords: Spatial variation; Variogram; Kriging; Mineral ores; Copper grade
Introduction
Geostatistics is the primary solution when it comes to modeling spatial data in an accurate and intelligent way, guaranteeing precision and reliability in results [1-4]. Geostatistical methods have been applied, among others, in geology of mineral deposits, applied geology, environmental geology, mining geology, mining, hydrogeology, environmental studies, soils sciences, geodesy, geography, agriculture, geochemistry, epidemiology, oceanography, meteorology, forestry, enzymology, power engineering (energetics) and other scientific disciplines and sectors of national economy [2-20].
Geostatistical techniques are the most efficient and powerful tools to characterize, estimate and manage mineral resource, optimize mineral resource management, estimate mineral resources in a robust way, classify your mineral resources, characterize resource uncertainties, optimize drill hole spacing, and validate model and achieve reconciliation [21-25]. Geostatistics offers a wide range of methodologies adapted to all commodities and styles of deposits. Geostatistical studies guarantee the quality of your evaluations at different stages of the development of the realized projects, i.e. from exploration to development, production and even for site remediation.
Many of the author’s previous scientific papers devoted to the modelling of the spatial variation in the Foresudetic Monocline copper ore deposit parameters and the estimation of their values, analysed the variation in Cu content and thickness of the (recoverable) deposit series within the post-mining blocks in the productive mines in the Lubin-Sieroszowice area, applying with geostatistical methods [9-12,26,27].
The values of semivariogram function γ(h), presented as both isotropic semivariograms and empirical directional semivariograms of the deposit parameters, showed that nugget effect C0 was a significant component (generally present) in the overall variation (expressed by total sill variance C) of the two deposit parameters [9,10]. The presence of the nugget effect C0 indicates sharp fluctuations (larger or smaller in scale) in the values of the deposit parameters. The percentage of the C0 effect, representing the random component in overall variation C, varied widely depending on the location of the analysed mining block in the Lubin-Sieroszowice area, which was due to the predominant type of lithological profile of the deposit series. But, nugget effect C0 of less or greater share, was always found to be present.
After the empirical semivariograms had been approximated with the theoretical models, then raster maps of the spatial distributions of the estimated averages Z* of the deposit parameters, showing their resultant (overall) variation within the surface boundaries of the postmining blocks, were calculated and plotted. However, so far it was not possible to plot the spatial distributions of averages Z*, separately for the individual components of the theoretical models and nugget effect C0 (the random component). As a result, the effect of the components on the total variation C of the deposit parameters, described by the theoretical models fitted to the semivariograms, so far wasn’t determined.
Hence the author came up with the idea of filtering the variation in the copper ore deposit parameters, successively removing the different components of the adopted theoretical models of the semivariograms [17-19].
It can be assumed that, if the fitted model of the semivariogram of a regionalized variable, i.e. a considered geological parameter of the deposit, consists of several basic nested structures, then the investigated regionalized phenomenon (the mineralization of the deposit series rocks with copper compounds) can be considered as a combination of several components co-occurring over different distances. Instead of evaluating the whole analysed regionalized phenomenon, the particular components of the adopted theoretical semivariogram model are filtered off. They can be filtered off (removed) by applying ordinary kriging or simple kriging [25,28,29].
One can consider the shorter range of influence (a), i.e. the component corresponding to a high frequency (small-scale variation) or the longer range of influence (a) of the semivariogram (large-scale variation) or the two ranges “a” simultaneously.
The author’s earlier experience in this regard was connected with filtering the components of complex theoretical semivariogram models of loads in the 220 and 400 kV power networks covering the area of Poland, carried out using the ordinary kriging technique [11].
This paper presents the results of spatial analyses showing in detail the structure of the variation in recoverable copper ore deposit copper content, thickness and accumulation (quantity) for post-mining block S-1 of the Sieroszowice mine in the Foresudetic Monocline in the Lubin-Sieroszowice area (SW part of Poland), carried out using the (isotropic, relative) variogram function and the ordinary kriging [17-19].
The stratified copper ore deposit occurs at the Rotliegend/ Zechstein borderline, copper sulphide mineralization comprises Weissliegend sandstones and Zechstein copper-bearing shales and dolomite rocks [8,26]. The deposit has a bed-like form, extends NWSE and is inclined at an angle of 3-5° towards NE.
Research Methods Used
Basic assumptions of geostatistics can be found in a such positions as Armstrong M et al. [1], Isaaks EH et al. [5], Matheron G et al.[3], Mucha J et al. [7,8], Namysłowska-Wilczyńska B et al. [9,10], Wackernagel H et al. [4].
The isotropic semivariogram function, the relative semivariogram function, the ordinary kriging estimator and the filtering of theoretical semivariogram model components, by means of ordinary (block) kriging were used to carry out the spatial analyses [17-19].
Semivariogram function
The empirical semivariogram, showing the correlation between variables arranged (ordered) on a (2D) surface, is expressed by the relation:
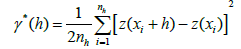 (1)
(1)
where:
γ*(h) - The semivariogram function value,
z(xi + h), z(xi) - Values in points xi and xi+h, separated by distance h,
nh - The number of pairs of values (xi, xi+h) in points separated by distance h, used to calculate semivariogram function γ*(h).
Relative semivariogram function
The relative semivariogram function is expressed as follows:
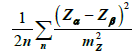 (2)
(2)
The general relative semivariogram is a measure normalized by the square of the sum of the mean values of the considered parameters, used for each semivariogram lag distance:
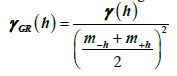 (3)
(3)
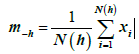 -the mean for the initial values of variable(4)
-the mean for the initial values of variable(4)
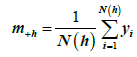 -the mean for the initial values of variable(5)
-the mean for the initial values of variable(5)
m*2– the square of the mean, m.
The general relative semivariogram is scaled by the f(m*) function of the global mean value or a local mean value estimate:
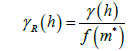 (6)
(6)
This kind of semivariogram is sometimes employed to eliminate the proportionality effect. Mostly the scaling function, i.e. the square of the mean (m), is used.
Ordinary kriging estimator
Kriging is an exact BLUE interpolator, i.e. a technique of estimating the weighted moving average for the estimation of parameter averages Z*, yielding the best unbiased linear estimates of point values or block averages Z* of the analysed regional variables at minimum estimation variance σk2 [1,3-5,7-10].
It is a mean value allocation technique used for the purposes of “local estimation” in which only the data located close to the estimation area are used in estimating. The values of the geostatistical empirical semivariogram model are calculated for the analysed area being the subject of estimation. Most often the following kriging estimators are used:
- ordinary kriging (when the arithmetic mean is unknown),
- simple kriging (when the arithmetic mean is known – has been estimated for the whole investigated sampling population or is obtained as a result of local estimations).
In ordinary kriging a constraint is imposed on weights, i.e. the sum should amount to 1. The value of an investigated parameter in location x0 is estimated using ordinary point kriging on the basis of n surrounding sampling points xα , linearly dependent on weights w:
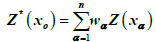 (7)
(7)
Whereas in simple kriging, arithmetic mean m is known has been calculated on the basis of the value of the regionalized variable.
Let us consider regionalized variable Y(x) with a mean of 0. The basic regionalized variable is obtained as Z(x) = Y(x) + m, as a result of adding constant component (term) m.
Estimator Y(x) is expressed as:
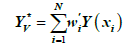 (8)
(8)
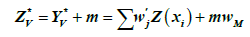 (9)
(9)
Filtering of Theoretical Variogram Model Components
The analysed regionalized variable Z can be considered as a linear combination of two variables: Y1 and Y2, called scale (range) components, and the mean:
Z = m + Y1 + Y2 (10)
Y1– the component is described by variogram γ1,
Y2– the component is described by variogram γ2.
If the two variables are independent, one can easily find that the variogram of variable Z is expressed by:
γ =γ1 +γ2 (11)
Instead of estimating the variogram of variable Z one can be interested in estimating one of the two components: γ1 or γ2. The estimate of one of the (scale) components is expressed as:
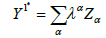 (12)
(12)
One should find out if the mean is a known quantity or not. If the mean is known, one should check whether the estimator unbiasedness condition is satisfied automatically, without imposing additional constraints on the kriging weights. If the mean is constant, but unknown, the unbiasedness condition leads to the equation:
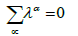 (13)
(13)
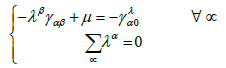 (14)
(14)
The estimation of the other scale (range) component Y2* is effected by simply replacing γ1 with γ2 in the right side of the system of kriging equations and leaving the left side of the system of equations unchanged.
One can also want to filter off this scale component. This is usually the case when measurements are made and noise (a random component) is found to occur.
It is assumed that the random component (noise) is independent of the variable and is described by its own scale component. When the noise effect (the random component) is removed, the kriging technique is used to estimate the variable component.
Since the system of kriging equations is linear, one can easily check that:
Z* = m* + Y1* + Y2* (15)
The presented filtering technique is not limited to two components per regionalized variable or to a single regionalized component. In the case of a larger number of variables, the components can be filtered using the co-kriging technique.
Range of Spatial Analyses
Spatial analyses of the variation in copper mineralization were carried out in the following stages1 [29]:
- calculation of the isotropic and relative semivariograms of the two deposit parameters: copper content [%], deposit thickness [m] and deposit accumulation (quantity q) [%mt/m2];
- approximation of the isotropic variograms of the deposit parameters, by means of composite theoretical models consisting of the cubic model, the spherical model and the nugget effect C0;
- estimation of the averages Z* and estimation standard deviation σk of the deposit parameters in the centres of the blocks of the elementary grid covering block S-1 of the Sieroszowice mine, using ordinary kriging;
- successive filtering off of the particular components of the composite theoretical models of the deposit parameter semivariograms, i.e. the random component (the nugget effect C0), the cubic model and the spherical model, and then the sum of the component models, and the estimation of averages Z* for the particular components, using ordinary kriging.
Statistical Analysis of Variation in Deposit Parameters Against Deposit Series Lithology in Block S-1
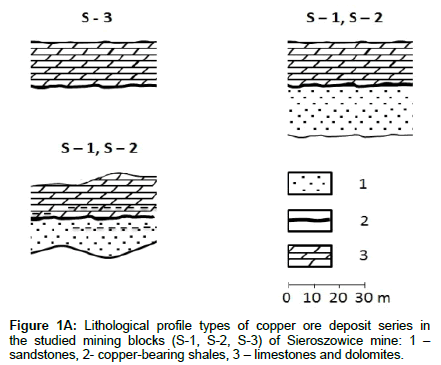
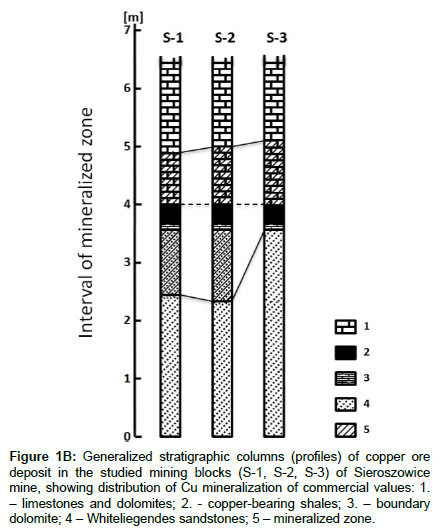
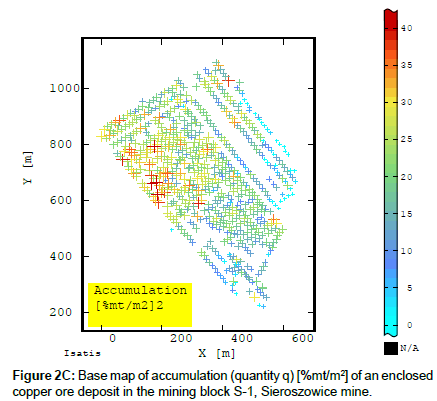
Post-mining block S-1, selected from three mining blocks (S-1, S-2, S-3) located in the Sieroszowice mine Namysłowska-Wilczyńska B et al. [9,10] in the Lubin-Sieroszowice area, was the object of the spatial analyses. The analyses were based on data obtained by sampling the deposit with groove samples mostly distributed uniformly (at a spacing of 15÷20 m), over the area of Sieroszowice mine block S-1, concerning the copper content in, the thickness of the (recoverable) deposit concentrated in Weissliegend sandstones, Zechstein copperbearing shales and calcareous-dolomitic formations, at a recoverability criterion of 0.7% Cu, and the deposit accumulation (Figures 1A-1B; Figures 2A - 2C). The recoverable deposit is represented here by the lithological series: sandstone ore, copper-bearing shales (incl. boundary dolomite) and carbonate ore.
Figure 1B: Generalized stratigraphic columns (profiles) of copper ore deposit in the studied mining blocks (S-1, S-2, S-3) of Sieroszowice mine, showing distribution of Cu mineralization of commercial values: 1. – limestones and dolomites; 2. - copper-bearing shales; 3. – boundary dolomite; 4 – Whiteliegendes sandstones; 5 – mineralized zone.
dolomite; 4 – Whiteliegendes sandstones; 5 – mineralized zone.
The deposit’s metallic mineralization is characterized by varied composition and diversity of forms. The major copper minerals are: chalcocite (Cu2S), bornite (Cu5FeS4), chalcopyrite (CuFeS2) and covellite (CuS). The minor copper minerals are: tetrahedrite (Cu12Sb4S13), tennantite (Cu12As4S13), cuprite (Cu20), enargite (Cu3AsS4) and stromeyrite (AgCuS). Also Pb and Zn minerals (PbS, ZnS) and silver (Ag) occur.
The mineralization within the studied block S-1 is characterized by non-uniform spatial distribution. There are subareas where the thickness of sandstone ore is greater than that of carbonate ore. Sometimes mineralization in dolomites appears as far as at 1.20 m, from the contact of these rocks with the top of copper-bearing shales. In some places sandstone rocks and carbonate (calcareous-dolomitic) rocks are mineralized in an almost equal interval. Also profiles with a very small deposit thickness, in which mineralization spread in the top layers of Weissliegend sandstones, copper-bearing shales and the bottom layers of Zechstein dolomites, were found.
The sandstone ore is in the form of light-grey Weissliegend sandstones with a carbonate-argillaceous, argillaceous and sometimes anhydrite-gypsum binder. The copper-bearing shales are represented by boundary dolomite, black shales, occurring in the bottom part of the shale series, and dolomitic shales (exhibiting partibility) in the roof part. The carbonate ore is made up of various (argillaceous, striated and calcareous) dolomites. The argillaceous dolomite thickness ranges from 0.1 m to 0.5 m. The striated dolomite constitutes a layer of greatly varying thickness (0.5 ÷ 2.0 m), with diminishing horizontal stratification. Fissures, open or filled with anhydrite or gypsum, occur within the calcareous dolomite.
Evaluation of Basic Statistics
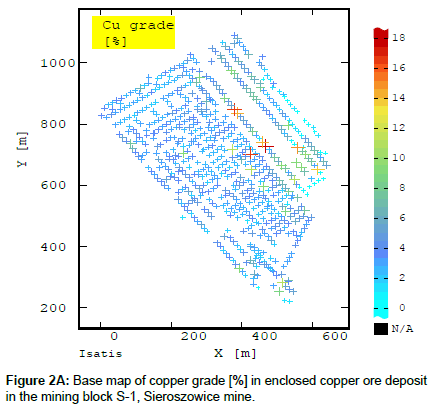
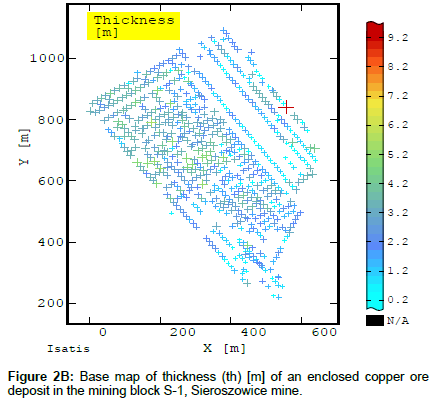
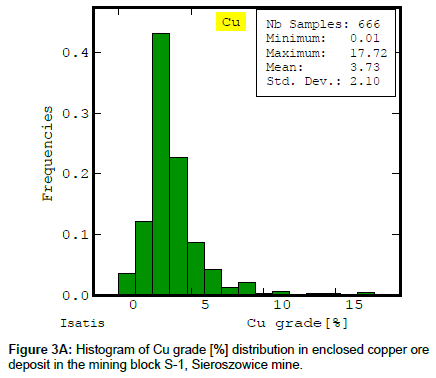
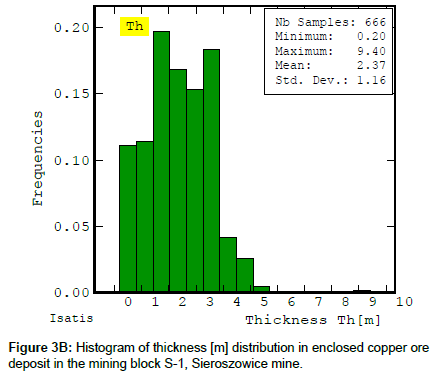
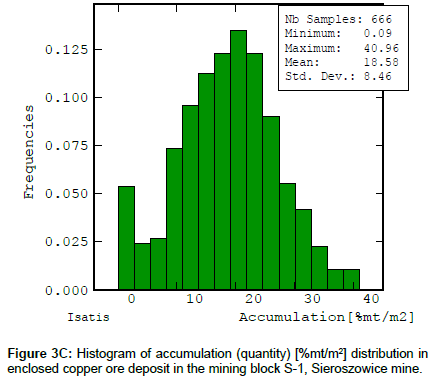
The basic statistics of the recoverable copper ore deposit parameters for block S-1 were estimated using a very large data sample size, amounting to n=666 (Figures 2A-2C and Table 1).
| Type of the ore | Thickness [m] | Cu grade [%] |
|---|---|---|
| Carbonate rocks | 2 | 2 |
| Copper-bearing shales | 0.2 ÷ 0.5 | 12 |
| Sandstone rocks | 3 | 2 |
| Whole deposit series | 2.37 | 3.73 |
Table 1: Mineralization spread in the top layers of Weissliegend sandstones, copper-bearing shales and the bottom layers of Zechstein dolomites.
The results of the principal statistical parameters indicate a great variation in copper content in the whole (recoverable) deposit series and a large variation, comparable with two other parameters, i.e. thickness and deposit accumulation (quantity) (Table 2).
| Deposit Parameter | Size n | Minimal value Xmin | Maximal value Xmax | Mean value | Standard deviation S | Variation coefficient V [%] |
|---|---|---|---|---|---|---|
| Copper grade Cu[%] | 666 | 0.01 | 17.72 | 3.73 | 2.1 | 56 |
| Thickness Th[m] | 666 | 0.2 | 9.4 | 2.37 | 1.16 | 49 |
| Accumulation(quantity) [% mt/m2] | 666 | 0.09 | 40.96 | 18.58 | 8.46 | 46 |
Table 2: A comparison of basic statistics of ledge parameters values for enclosed copper ore deposit in block S-1 of Sieroszowice mine.
The copper content ranged widely from 0.01% Cu (min. value) to 17.72% Cu (max. value) (Table 2). Also the high value of standard deviation S and the higher value of this parameter’s variation coefficient V are noticeable.
The statistical range of deposit thickness is also considerable (0.20÷9.40 m), but not as wide as in the case of Cu content (Table 2). The variation coefficients (V) indicate that values of the two deposit parameters vary greatly, with Cu content varying more (Table 2).
The variation coefficient (V) of accumulation (quantity q) is comparable to statistics (V) of thickness (Table 1).
The confidence intervals for the studied deposit parameters, assuming level of significance α = 0.05, have been presented below:
A confidence interval for unknown mean m
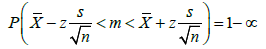
where:
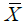 - Arithmetical mean,
- Arithmetical mean,
S - Standard deviation,
n- Size of statistical sample,
m - Uknown true (average) value of deposit parameter,
z - Confidence coefficient determined from tables of normal distribution for the assumed level of significance α (P = 0.95 %).
A confidence interval for unknown mean m of Cu grade [%]
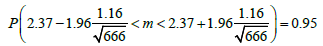
P(3.73 - 0.16< m < 3.73+ 0.16) = 95%
P(3.57 < m < 3.89) = 95%
A confidence interval for unknown mean m of thickness [m]
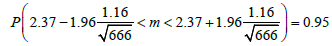
P(2.37 - 0.09< m < 2.37+ 0.09) = 95%
P(2.28 < m < 2.46) = 95%
A confidence interval for unknown mean m of accumulation (quantity q) [%mt/m2]
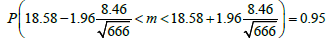
P(18.58 – 0.6424 < m < 18.58 + 0.6424) = 95%
P(17.9376 < m < 19.2224) = 95%
Distribution histograms
The Cu content distribution histogram is unimodal and peaked, with tendency showing evident positive skewness, which manifests itself in the presence of secondary classes with an elevated concentration of Cu compounds, but the percentage share of the classes is small (Figure 3A). This shape of the histogram is corroborated by the relatively high value of skewness coefficient g1, indicating a strong asymmetry and the high value of kurtosis coefficient g2.
The deposit thickness distribution histogram is bimodal (Figure 3B). The value of coefficient g1 is very low (quasi-symmetry) while the low kurtosis coefficient g2 indicates a rather flat character of the histogram and a concentration of classes, i.e. the occurrence of bimodal classes with an almost equal share. The accumulation distribution histogram is also bimodal, with the prevailing one modal class, showing very small values of the negative skewness g1, and the kurtosis g2 (Figure 3C)
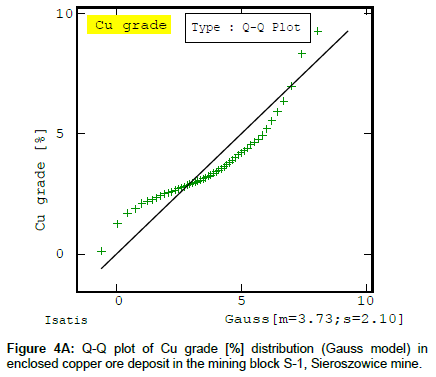
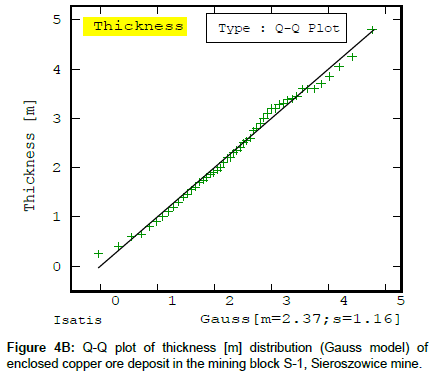
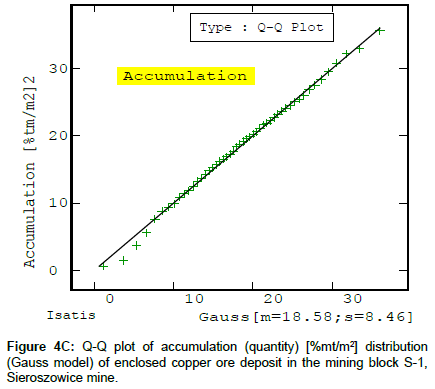
It appears from the Q-Q diagrams of the deposit parameters (Figures 4a-4c) that their values fit the theoretical distribution to a different degree: the Cu content diagram fits the Gaussian distribution less exactly (Figure 4a) while the deposit thickness diagram’s fit (Figure 4B) and the deposit accumulation diagram’s (Figure 4C) are almost perfect, as indicated by the positive skewness coefficients g1 of the deposit parameters.
Investigation of correlation between deposit parameters
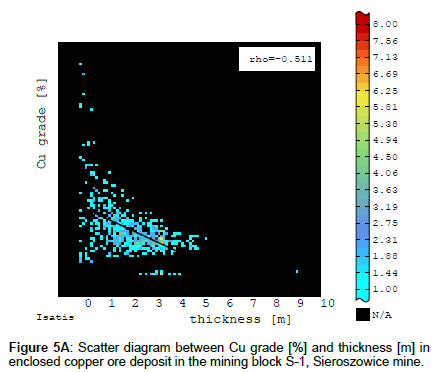
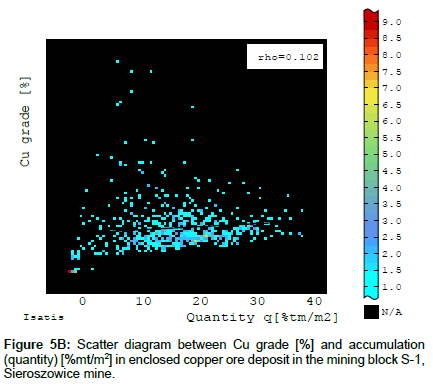
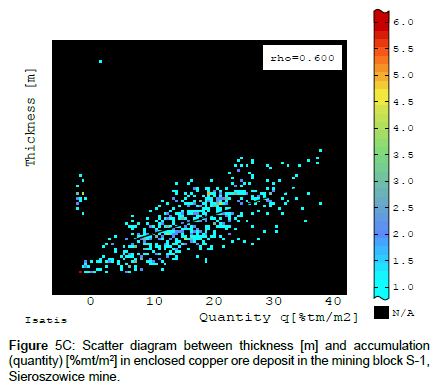
A search for a correlation between the deposit parameters, i.e. the Cu content in the recoverable deposit and the thickness of this deposit, shows that there is a negative correlation, (characterized by correlation coefficient r ~ - 0.511), within block S-1 (Figure 5A), observed in some areas of Lubin-Sieroszowice region, described in different works on variability of the copper deposit in the Foresudetic Monocline, among others [6,9,10,26]. Subareas of small deposit thickness, associated with the occurrence of only copper-bearing shales or shales and including roof sandstone layers or bottom carbonate rock layers, correspond to the subareas of intensive copper mineralization (high Cu content) within block S-1 and vice versa. Subareas of big deposit thickness corresponds mineralization, occurring in sandstones or carbonates and also in both kinds of rocks. There is a positive correlation between the deposit thickness and its accumulation (quantity), characterized by correlation coefficient r ~ 0.60 (Figure 5B and 5C).
Modelling of Semivariograms
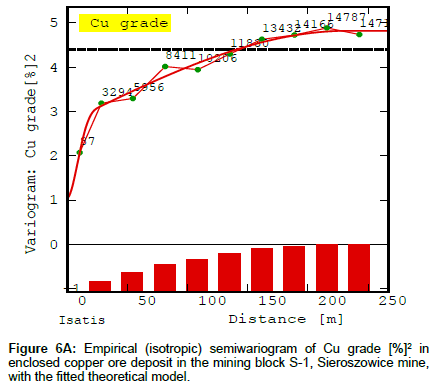
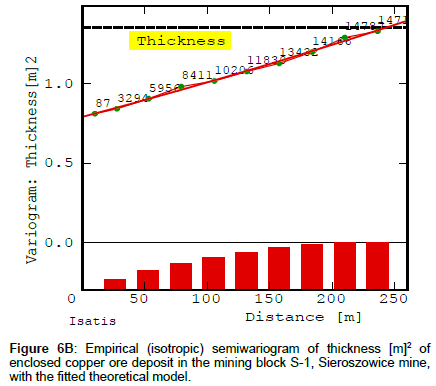
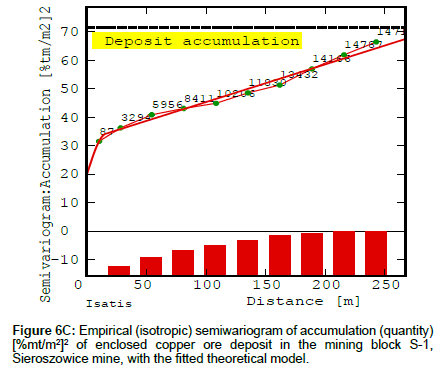
The determined semivariograms of the analyzed deposit parameters reflect the varied character of the variation in Cu content and deposit thickness along the analysed distance of 250 m. The tendency towards non-random variation in semivariogram function γ(h) is visible for both parameters, but in the case of Cu content it is steep throughout the diagram, sharper at its beginning (Figure 6A). In the case of the deposit thickness semivariogram and accumulation semivariogram, there is a very strong variation trend expressed- the value of function γ(h) steadily increases (Figures 6B and 6C).
Figures 6A-6C show empirical isotropic semivariograms modelled using composite theoretical models consisting of the nugget effect, the cubic model and the spherical model. The parameters of the models are presented in Table 3. One can notice that the semivariograms show the nested character of the variation in the deposit parameters. Changes occur over a very short distance, as described by the spherical model, over a shorter distance (Cu content, accumulation) and over a very long distance (deposit thickness), as described by the cubic model. The nugget effect (C0) of Cu content and accumulation was more clearly evident in the total variation (C) than the nugget effect of deposit thickness, which was slightly smaller (Figures 6A-6C).
| Deposit parameter | Nugget effect C0 | Partial sill variance C’ | Total sill variance C | Range of influence a [m] | Basic model structures |
|---|---|---|---|---|---|
| Copper grade [%]2 | 1.0433 | 1.7054 2.0725 | 4.8212 | 233.1896 29.3838 | nugget efect cubic spherical |
| Thickness [m]2 | 0.7901 | 387.1062 18. 1127 | 405.2189 | 53953.60 13531.60 | nugget efect cubic spherical |
| Accumulation [%*m*2.45t/m2]2 | 19.8570 | 5.0424 7.2248 32.1350 | 64.2591 | 16.20 15.20 243.00 | nugget effect spherical spherical linear |
Table 3: A comparison of geostatistical models of isotropic semivariograms of ledge parameters for copper ore deposit in block S-1 of Sieroszowice mine.
Quantities of components: of random variation component (UR) and non-random component (UN-R) in the total observed variability of three studied deposit parameters, were determined for the distance h1 between the observations [7].
It turns out that the random component (UR) has similar limits, namely from 23.69 ÷ 27.74% for two parameters - Cu grade and accumulation (quantity q) for S-1 block of Sieroszowice mine. The highest value of the UR component is achieved in the case of the deposit thickness, i.e. 58.52%.
Non-random component (UN-R) values are contained from 41.4815 % (thickness) to 76.3098 % (Cu grade, accumulation).
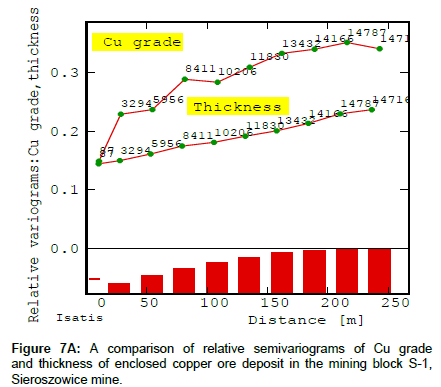
The relative semivariograms of the two parameters (Cu grade, thickness), presented together in Figure 7A, show very well the above tendencies in the variation of the analysed parameters. These are sharp marked changes in increasing values of the relative semivariogram function γ(h) of Cu grade and much gentler changes in gradually increasing values of deposit thickness semivariogram function γ(h).
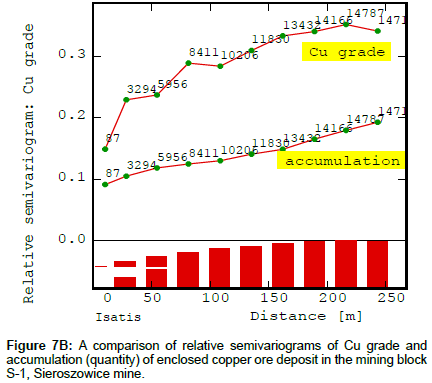
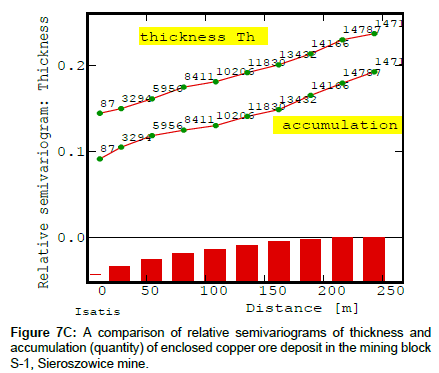
The course of relative semivariograms, respectively Cu grade and accumulation (Figure 7B) and thickness and accumulation (Figure 7C) were also compared. Relative semivariograms of these parameters are clearly different. In the case of the Cu grade, the values of γ(h) function strongly increase with the distance, while, with respect to accumulation, they are significantly less pronounced, increasing only more clearly, at the end of the course (Figure 7B). Meanwhile, the relative semivariograms of thickness and accumulation are parallel to each other, indicating the almost identical nature of the changes (Figure 7C).
Results of Estimation
In this stage of the studies the analysed block S-1 was covered by the spatial elementary grid. The following elementary grid dimensions were assumed: the number of grid nodes-67 along the X-axis and 47 along the Y-axis; the total number of nodes-N = 67 × 47 = 3149 and the grid’s mesh dimension were amounted to-0.5 × 1 = 200 m2.
The basic geostatistical parameters, i.e. the estimated averages Z* and estimation standard deviation σk of the deposit parameters, were estimated in the nodes of the grid. The estimation covered 3149 grid nodes and 2430 were actually estimated. The results of the global estimation of the deposit parameters and the results of the filtering of the components of the theoretical semivariogram models are grid data obtained for the nodes (centres) of the adopted elementary grid. Because of the ordinary kriging technique used, these are smoothed values.
The results of the global estimation of the copper ore deposit parameters are presented in Tables 4,5 and the results of the filtering semivariogram model components are shown in Tables 5,6.
| Deposit parameter | Number of grid nodes N | Minimal value Xmin | Maximal value Xmax | Mean value | Standard deviation | Variation coefficient V [%] |
|---|---|---|---|---|---|---|
| Estimated averages Z* [%] | 2430 666* |
0.49 0.01* |
11.95 17.72* |
3.63 3.73* |
1.22 2.10* |
34 56* |
| St. deviation of estimation σk [%] | 2430 | 0.56 | 2.05 | 1.18 | 0.36 | 30 |
Table 4: Global statistics of estimated values Z* of Cu grade [%] in enclosed copper ore deposit in block S-1 of Sieroszowice mine*
| Deposit parameter | Number of grid nodes N | Minimal value Xmin | Maximal value Xmax | Mean value | Standard deviation | Variation coefficient V [%] |
|---|---|---|---|---|---|---|
| Estimated averages Z* [m] | 2430 666 |
0.67 0.20 |
3.89 9.40 |
2.24 2.37 |
0.70 1.16 |
31 49 |
| St. deviation of estimation σk [m] | 2430 | 0.23 | 0.76 | 0.36 | 0.14 | 38 |
Table 5: A comparison of basic statistics of estimated values of thickness [m] of copper ore deposit in block S-1 of Sieroszowice mine**.
| Deposit parameter | Number of grid nodes N | Minimal value Xmin | Maximal value Xmax | Mean value  |
Standard deviation S | Variation coefficient V [%] |
|---|---|---|---|---|---|---|
| Estimated averages Z* [%*m*2.45t/m2] | 2430 | 0.40 | 32.56 | 17.10 | 6.68 | 39 |
| St. deviation of estimation σk [%*m*2.45t/m2] | 2430 | 2.02 | 6.07 | 3.28 | 0.96 | 29 |
Table 6: A comparison of basic statistics of estimated values of accumulation (quantity) [%*m*2.45t/m2] of copper ore deposit in block S-1 of Sieroszowice mine**
The values of the variation coefficients V of estimated averages Z* for the two parameters are in comparable ranges, with Cu grade showing greater variation, and with the accumulation indicating greatest variability (Tables 4-6). The values of the variation coefficient V of standard deviation σk are in a similar range, with coefficient V being slightly higher for the deposit thickness parameter.
Results of estimating deposit parameters with composite theoretical models of semivariograms taken into account
The results of estimating the basic geostatistical parameters are presented below on raster maps (Figures 8A-10B) and in tables (Tables 4-5), taking into account the composite theoretical semivariogram models and then the individual components of the fitted semivariograms models (Figures 6A - 6C, Table 3).
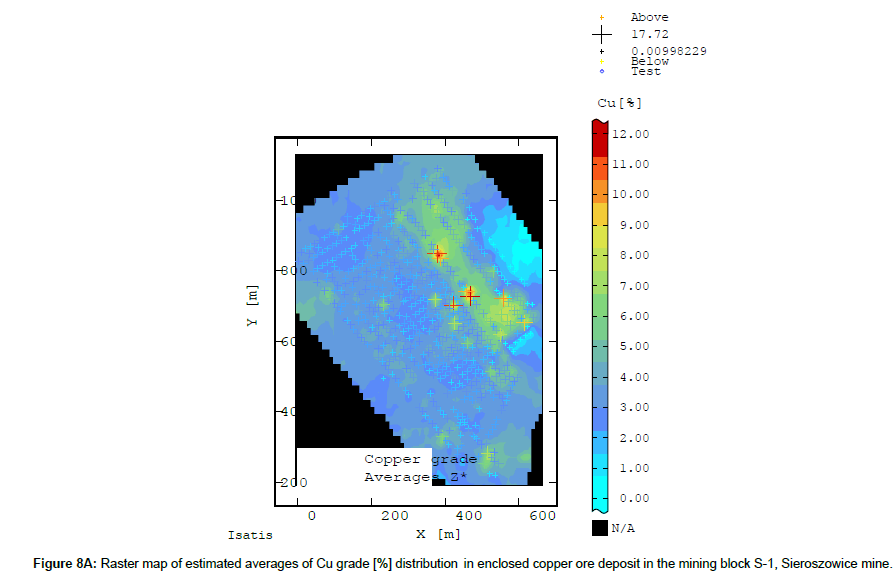
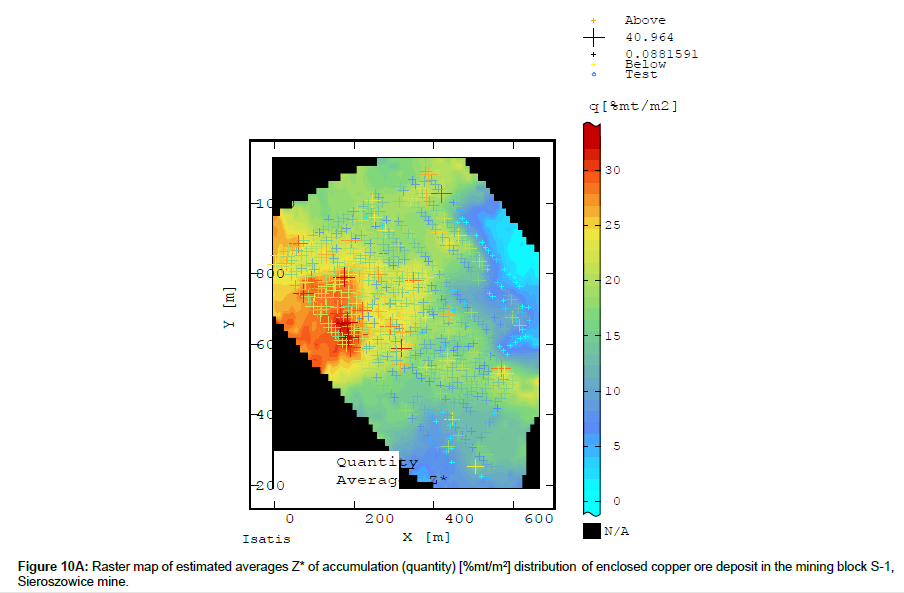
On the map showing Cu content averages Z*, in the NE, central and E part of block S-1 one can notice elevated averages Z* (Figure 8A), forming a relatively long band of richer copper mineralization (6.75-8.63% Cu). The band extends along the NW-SE direction (Figure 8A).
Several small centres of extreme mineralization can be distinguished in this band. Enclaves of richer mineralization occur within block S-1. Near the periphery of block S-1 a subarea of very low Cu content extends parallel to the high Cu content band along the same NW-SW direction (Figure 8A).
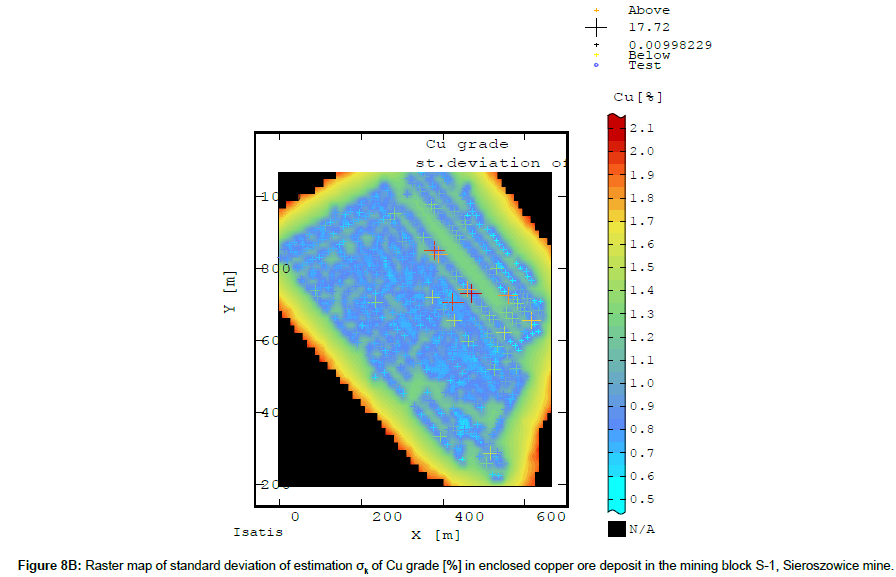
On the raster map showing the estimated values of estimation standard deviation σk the Cu content values are relatively even, ranging from 0.5 to 0.9% within the whole area of block S-1 (Figure 8B).
The values of standard deviation σk visibly increase (to 1.3- 1.5%) in the unsampled area in and on the peripheries of block S-1, extending along the NW-SE direction (Figure 8B).
Comparing the original values of weighted Cu content averages, determined for the groove samples taken from different locations within block S-1, with estimated Cu content averages Z* calculated in the elementary grid nodes one notices that the average based on the averages Z* in the elementary grid nodes is slightly lower than for the original data (Table 4). Whereas the minimum and maximum values and variation coefficient V of estimated average Z* are smoother and reach clearly lower values relative to the original data, which is undoubtedly due to the ordinary kriging technique used.
The star * shows basic statistics calculated on the basis of original values of the deposit parameter (Cu grade).
11.1.1.Uncertainty estimation: A confidence interval for mean value 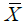 calculated on the basis of estimated averages Z* of Cu grade [%]:
calculated on the basis of estimated averages Z* of Cu grade [%]:
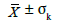
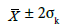
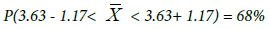
P(2.46< 3.63 < 4.80) = 68%
P(3.63 – 2.34 <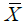 < 3.63 + 2.34) = 95%
< 3.63 + 2.34) = 95%
P(1.29 < 3.63 < 5.97) = 95%
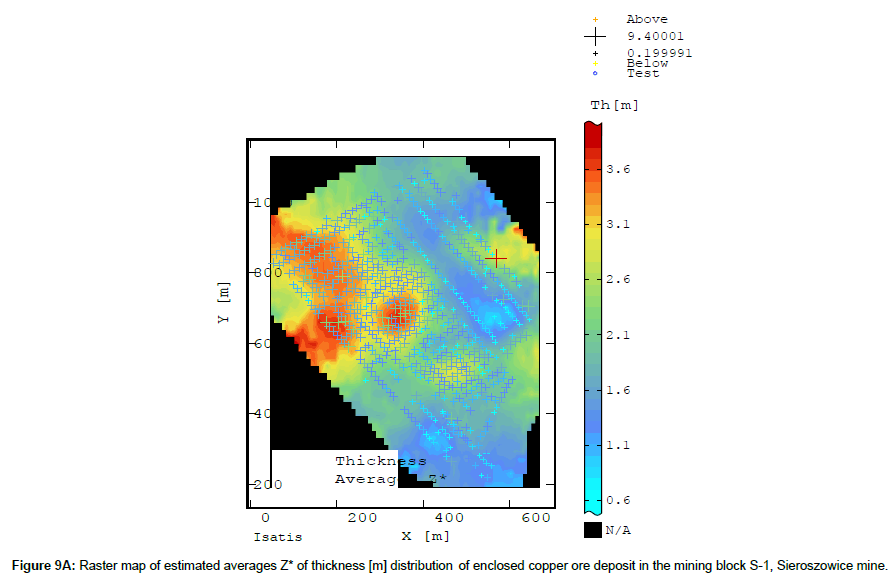
A relatively large subarea, occurring in the NW and W part of block S-1, extends along the NW-SE line on the raster map of deposit thickness averages Z* (Figure 9A). Averages Z* in this area range from 3.28 to 3.90 m. A subarea of lower deposit thickness averages, ranging from 0.60 to 1.42 m (Figure 9A), corresponds to the mentioned above subarea of rich Cu mineralization extending along the NW-SE line. It is also visible in the E part of block S-1 (Figure 9A). Small deposit thicknesses (0.60-1.42 m) also occur in the SW part of block S-1. In the E part of block S-1 there is an area of larger deposit thicknesses (Figure 9A), corresponding to the subarea of lower Cu content values (Figure 9A). A certain periodicity of deposit thickness variation is discernible in the whole block S-1 (Figure 9A).
Uncertainty estimation: A confidence interval for mean value 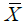 calculated on the basis of estimated averages Z* of thickness [m]:
calculated on the basis of estimated averages Z* of thickness [m]:
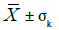
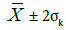
P(2.24 - 0.36 <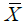 < 2.24+ 0.36) = 68%
< 2.24+ 0.36) = 68%
P(1.88 < 2.24 < 2.60) = 68%
P(2.24 – 0.72 <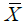 < 2.24 + 0.72) = 95%
< 2.24 + 0.72) = 95%
P(1.52 < 2.24 < 2.96) = 95%
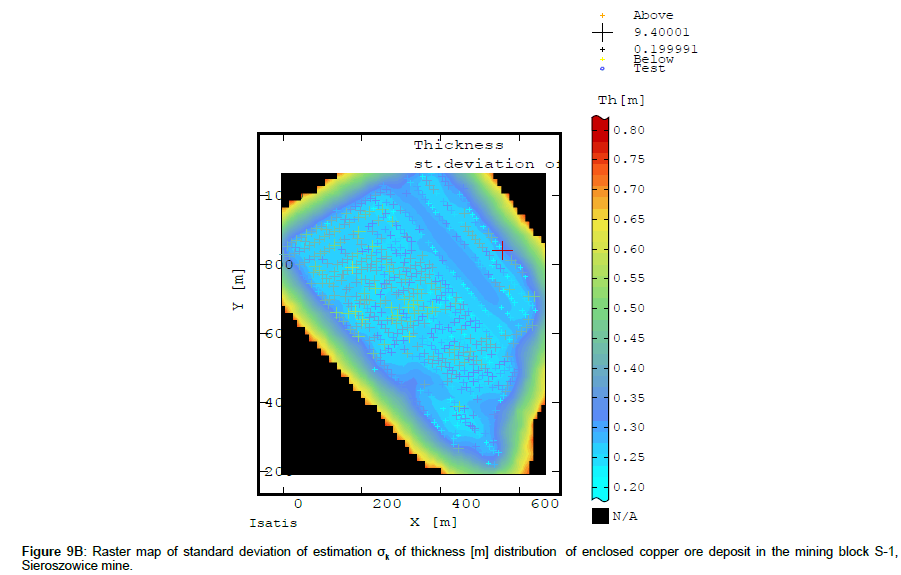
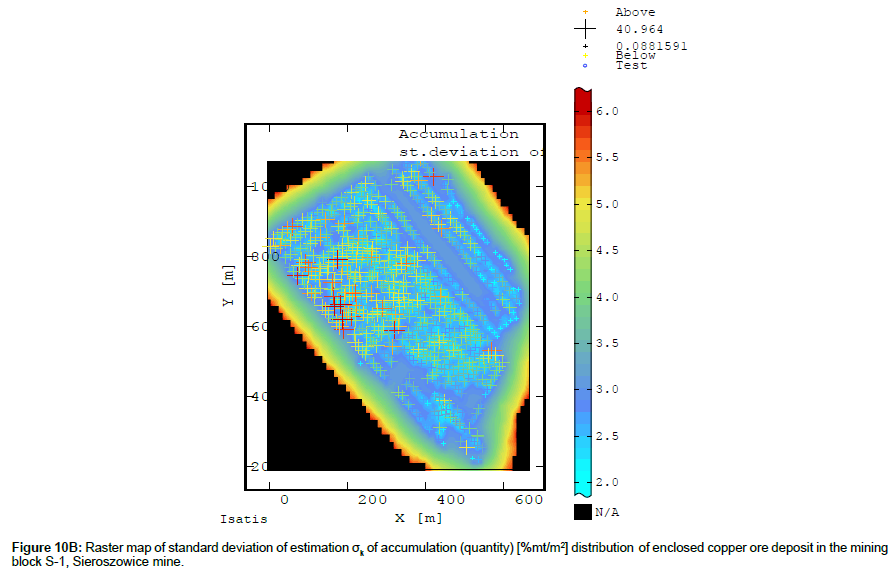
The raster map of the distribution of the values of recoverable deposit thickness estimation standard deviation σk shows a very even variation level. Standard deviation σk ranges from 0.20 to 0.25 m and from 0.25 to 0.275 m (Figure 9B). Towards the outer boundaries of block S-1 the values of σk become higher, ranging from 0.25 to 0.35 m and then from 0.50 to 0.60 m. Similarly as in the case of Cu content, the unsampled subarea extending along the NW-SE line in block S-1 is characterized by higher deposit thickness standard deviation (σk) values (0.325-0.37 m).
When one compares the original deposit thicknesses determined for the groove samples taken in different locations within block S-1 with the deposit thickness averages Z* calculated in the nodes of the elementary grid, it becomes apparent that the average determined on the basis of the averages Z* in the nodes is lower than the average based on the original data (Table 5). The minimum estimated average Z* reaches a much higher value, whereas the maximum average Z* and coefficient V based on averages Z* are lower in comparison with the original data.
The star * shows basic statistics calculated on the basis of original values of the deposit parameter (thickness).
Estimation of estimated values of accumulation (quantity) was performed on the basis of the calculations carried out for the assumed geostatistical model of semivariogram of accumulation (quantity), consisting of spherical, spherical & linear models (Table 6).
Uncertainty estimation: A confidence interval for mean value 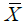 calculated on the basis of estimated averages Z* of accumulation (quantity) [%*m*2.45t/m2]:
calculated on the basis of estimated averages Z* of accumulation (quantity) [%*m*2.45t/m2]:
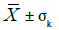
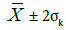
P(17.10 – 3.28 < 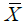 < 17.10 + 3.28) = 68%
< 17.10 + 3.28) = 68%
P(13.82 < 17.10 < 20.38) = 68%
P(17.10 – 6.56 <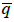 < 17.10 + 6.56) = 95%
< 17.10 + 6.56) = 95%
P(10.54 < 17.10 < 23.66) = 95%
Average unit quantity q (productivity) of the deposit:
qi = mi × γOi × pi × 0.01 [t/m2],
Quantity Q of the resource
Q = F ×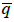
Limits of confidence interval for the resource quantity Q (for the significance level α = 0.05):
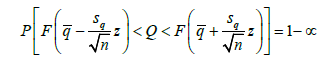
where:
mi [m], pi [%], γOi [t/m2] – suitably deposit thickness, percentage content of useful component, spatial density of the mineral,
F- surface of area under subject (area of the calculation area),
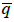 - average unit quantity of deposit (productivity of useful component from the surface 1m2 of deposit),
- average unit quantity of deposit (productivity of useful component from the surface 1m2 of deposit),
Q – resource quantity,
sq – standard deviation of quantity q,
z – confidence coefficient, determined from the tables of normal distribution for the assumed level of significance (z=1,96, α=0.05),
α – level of significance,
n – size of sample (the analyzed sample subpopulation);
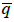 ± 2sq – upper and lower limit of confidence interval for P=95 %.
± 2sq – upper and lower limit of confidence interval for P=95 %.
Resource quantity Q
Q = 0.19 t/m2 × 480000 m2 = 91200 t
88283 t < 91200 t < 94116 t
The results of the global estimation, i.e. the tables and the also the raster maps showing the spatial variation in the values of the deposit parameters (Cu grade-Table 4; Figures 8A - 8B, thickness- Table 5; Figures 9A - 9B; accumulation (quantity)-Table 6; Figures 10A - 10B) were compared with the results of the partial components for particular components (Cu grade - Table 4; Figures 11A - 11D; thickness - Table 5; Figures 12A - 12D).
Results of filtering components of theoretical semivariogram models of deposit parameters
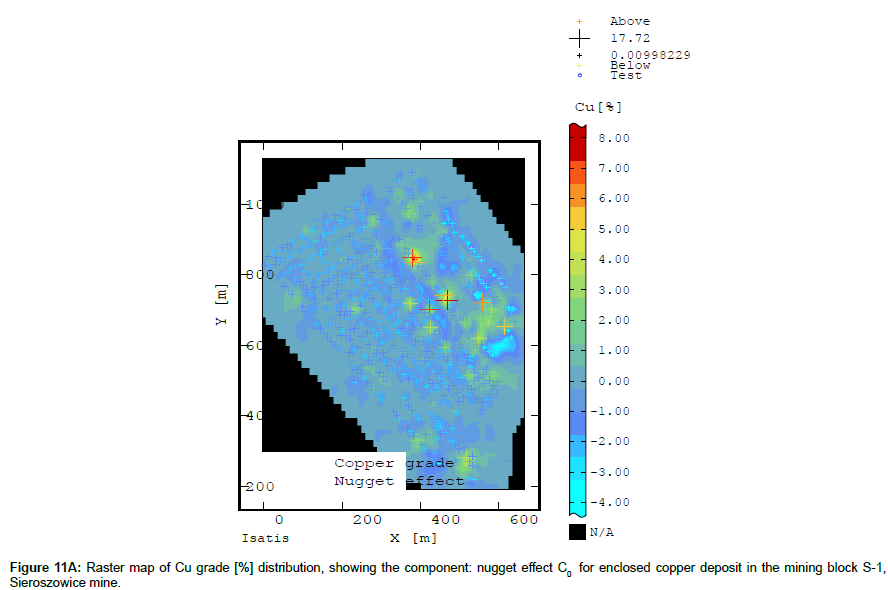
On the raster map showing the estimated averages Z* of nugget effect C0 (Figure 11A) one can precisely identify the zones (subareas) of elevated Cu content within block S-1 (and so enrichments and impoverishments in Cu content) and the scale and range of averages Z*.
It should be noted that the proportion of nugget effect C0 (Figure 11A) in the overall variability C of Cu content is significant (Figure 8A).
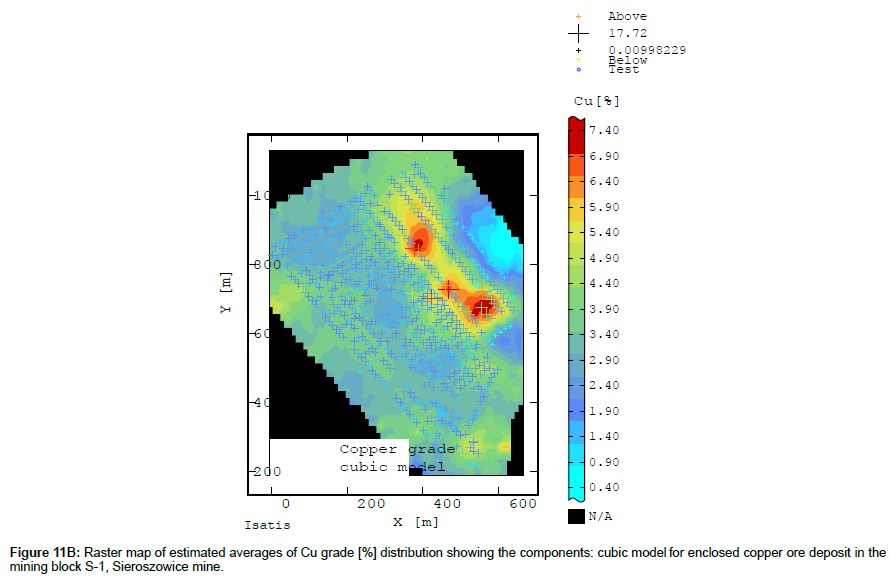
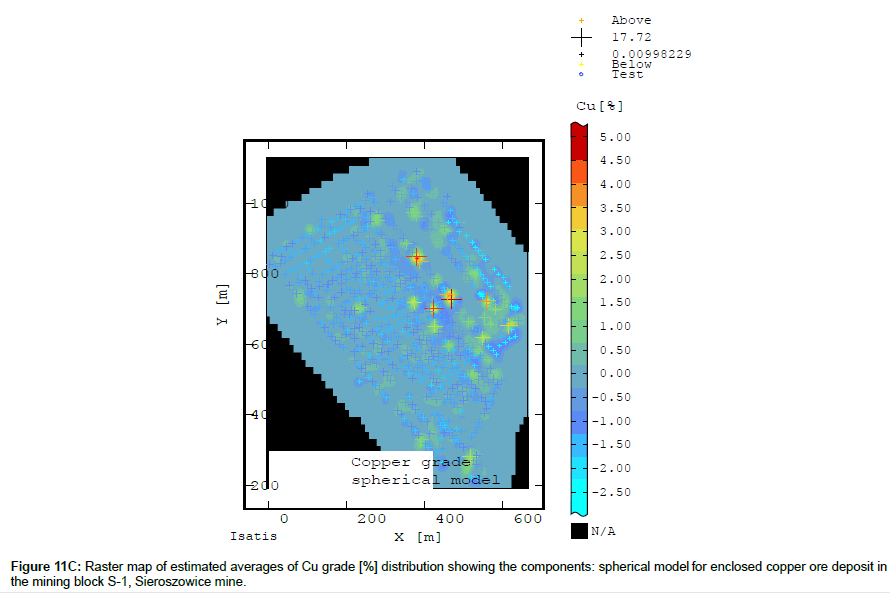
The large-scale changes (and so the low frequency of change of averages Z*) are represented by the cubic model of the Cu content semivariogram (Figure 11B) while the small-scale changes (and so the high frequency of change) are expressed by the spherical model of the Cu content variogram (Figure 11C).
It should be noted that the changes of averages Z*, represented by the spherical model of the Cu content semivariogram (i.e. the high frequency), amount to a significant percentage of the overall variation (C) of this parameter (Figure 11C).
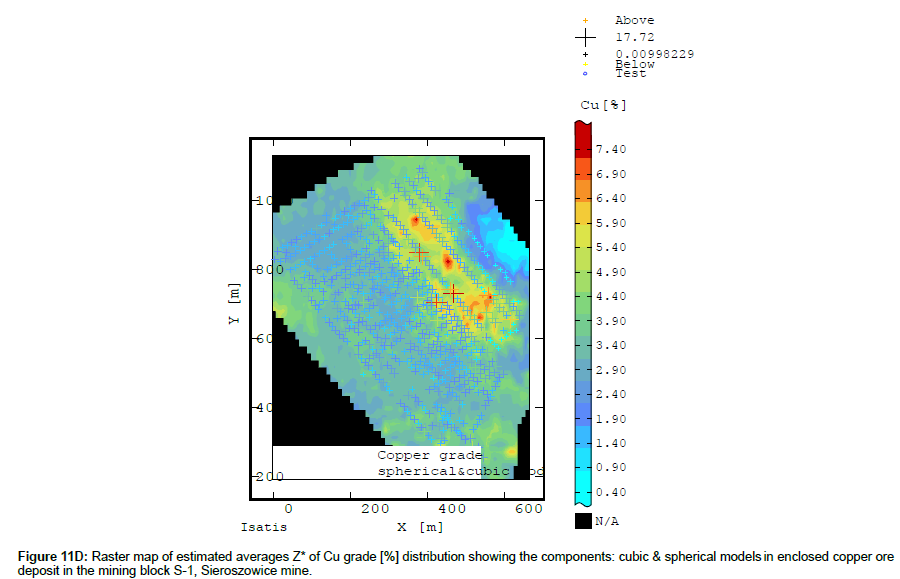
The raster map calculated on the basis of the sum the spherical model and the cubic model of the Cu content variograms shows a more detailed picture of Cu variation, where one can trace both small-scale and large-scale changes in averages Z* (Figure 11D).
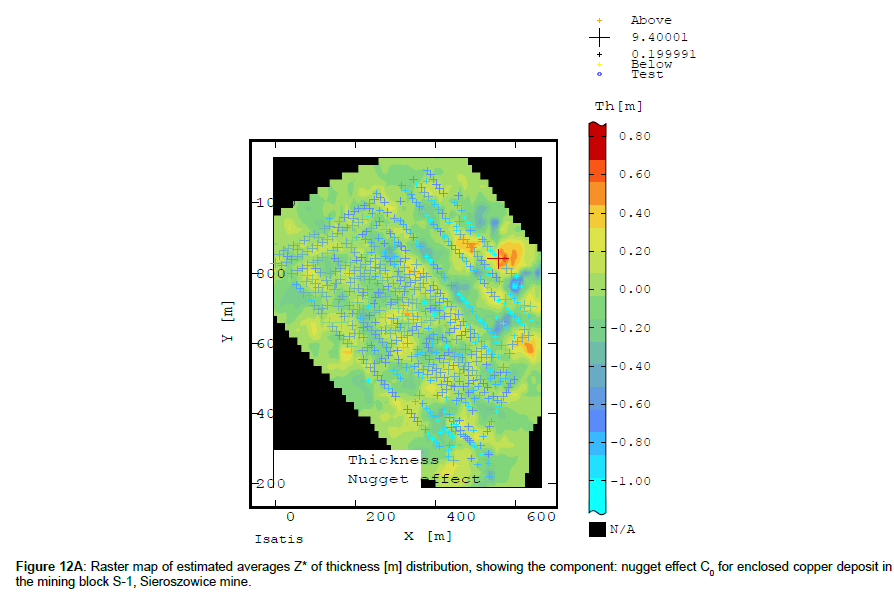
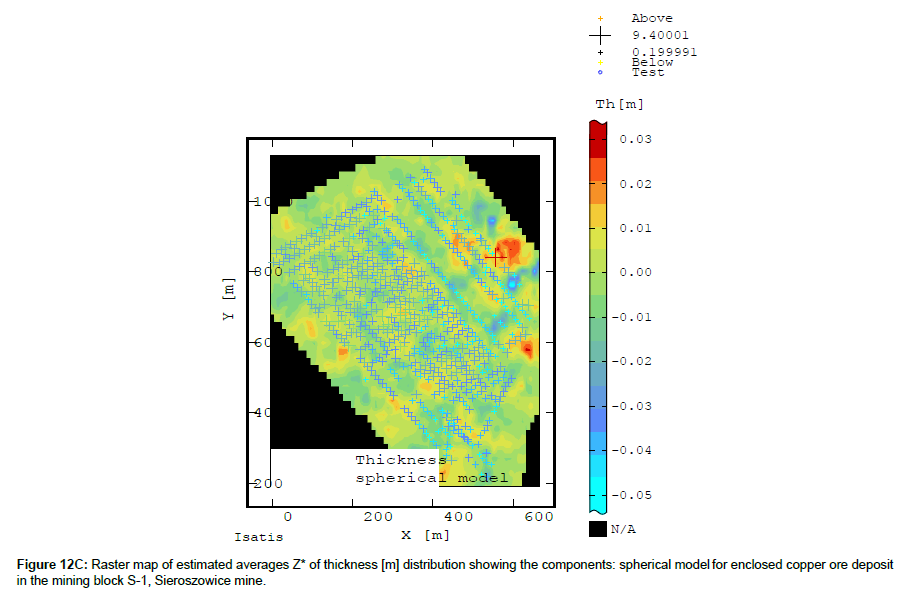
On the raster map showing the estimated averages Z* of nugget effect C0 (Figure 12A) one can precisely identify the zones (subareas) of much elevated or reduced recoverable deposit thickness within block S-1, the scale and range of this parameter. A high proportion of C0 indicates the places of so large thicknesses or small thicknesses of the balance ore.
In general, the proportion of nugget effect C0 (Figure 12A) in the total variation C of thickness (Figure 9A) is small, as opposed to the nugget effect C0 share, which was presented for Cu grade in raster map (Figures 8A,11A).
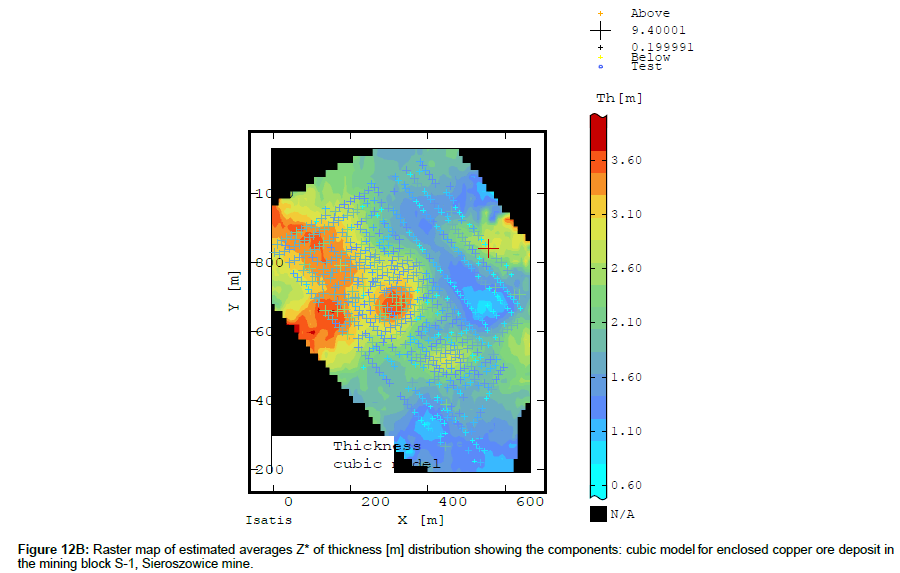
The cubic model of the deposit thickness semivariogram represents the large-scale changes (Figure 12B), while the smallscale (high frequency) changes are expressed by the spherical model of the thickness semivariogram (Figure 12C). The percentage of the variation expressed by this model of semivariogram is very small, reaching minimum values level.
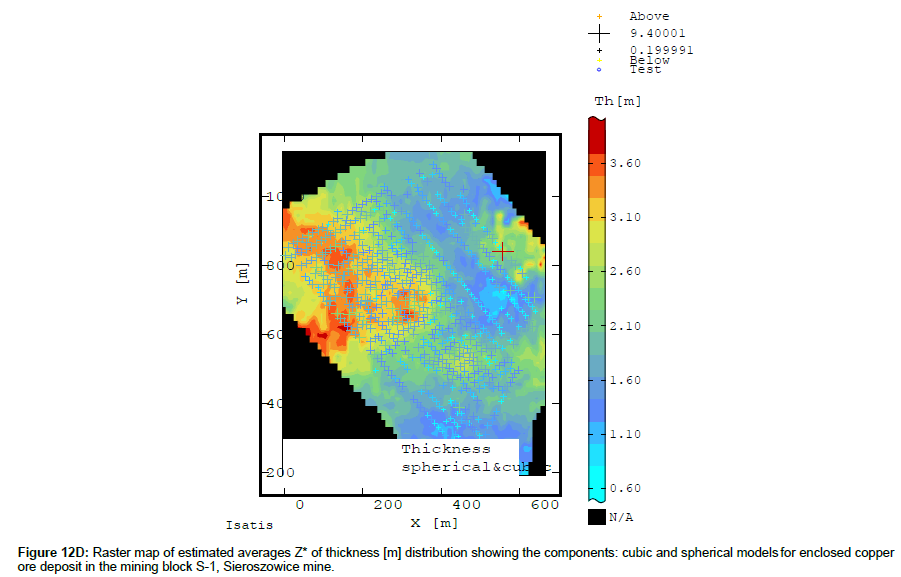
The raster map calculated using the sum of the two models (spherical and cubic) of deposit thickness semivariograms shows a more detailed picture of the variation of this parameter, where one can trace the varied character of both the large- and small-scale changes (Figure 12D).
It is apparent that the percentage of the spatial distribution of nugget effect C0 (Figures 11A-12A) in the overall variation (C) of the analysed deposit parameters (Figures 8A-9A)varies. In the case of Cu content, one should note the significant share of nugget effect C0, observed in many subareas of mining area S-1 (Figure 11A),whereas in the case of deposit thickness, the share of this effect in overall thickness variation C is much smaller, but it is also present in different parts of block S-1 (Figure 12A).
On the raster maps of the filtering results, showing images of spatial variation for the different components of the theoretical variogram models of the deposit parameters, one can trace the range of small- and large-scale changes in deposit parameter values (Figures 11-12).
Enrichment zones (characterized by elevated Cu content values), forming an elongated subarea extending along the NW-SE direction, occur within block S-1. This subarea may indicate the path of the secondary migration of ore-bearing solutions along the faults and the NW-SE and NNW-SSE fissures transecting the rocks of the deposit series. The fissures are filled with copper mineral veins.
The nugget effect C0 visible in the variograms is due to the occurrence of aggregates and large metallic concentrations. One cannot exclude the occurrence of additional enrichments in Cu sulphides, appearing in places where the NW-SE and NE-SW systems of fissures intersect.
Similar observations apply to the shape of the subarea of elevated recoverable deposit thickness. The subarea tends to extend along the NW-SE direction, but it is wider and not so much elongated as the subarea of elevated Cu content.
Conclusion
The structure of the variation in the basic parameters of the recoverable copper ore deposit has been explored in detail for block S-1 of the Sieroszowice mine. The results of this exploration contribute significantly to the solution of geological and mining problems.
The results of the geological modelling and estimation pertain to a particular lithological deposit profile, i.e. the one concentrated in the Weissliegendes sandstones, Zechstein copper-bearing shales and carbonate rocks. They show the character and degree of the predominant variation in the values of the investigated deposit parameters within mining block S-1.
A new investigative approach, consisting in filtering the individual components of the semivariogram models of deposit parameters by means of geostatistics (the estimation kriging techniques), has been adopted. This approach can be employed to investigate other geological, hydrogeological and geotechnical problems, especially in cases when the precise description of the spatial variation in such parameters is essential.
In the presented example of the estimation of copper ore deposit parameters, also the practical merits of the estimates are very important, considering that they are highly useful in the optimization of the directions of mining the deposit as well as in mining quality control and mining production planning.
The profitable extraction of deposits becomes increasingly more difficult and risky for various reasons, such as: the lower metal content, the greater hardness of the minerals and rocks, the greater mining depth and the higher delivery costs. Therefore ever more advanced modelling and simulation techniques are needed in order to enable a wider and more detailed analysis of possible scenarios.
1The studies were conducted using statistical and geostatistical software package ISATIS 2017 (the Isatis version 2017.1) made by Geovariances Firm, Avon-Cedex–Fontainebleau, France; www.geovariances.com [25,28-29].
References
- Armstrong M (1998) Basic Linear Geostatistics. Springer Science & Business Media, USA.
- Armstrong M, Matheron G (1987) Geostatistical Case Studies. Springer Science & Business Media, USA.
- Matheron G (1987) Geostatistical Case-Studies (Quantitative) Geology and Geostatistics. Springer, USA.
- Wackernagel H (1998) Multivariate Geostatistics: An Introduction with Applications. Springer, Berlin.
- Isaaks EH, Srivastava RM (1989) An Introduction to Applied Geostatistics. Oxford University Press, USA.
- Kotlarczyk J, Nieć M, Namysłowska-Wilczyńska B (1981), Model zmienności złoża rud miedzi Lubin- Polkowice i problemy jego genezy, Prace Geologiczne PAN, Oddział w Krakowie, Komisja Nauk Geologicznych.
- Mucha J (1994) Metody geostatystyczne w dokumentowaniu złóż. Skrypt Akademii Górniczo-Hutniczej w Krakowie. Wydział Geologii, Geofizyki i Ochrony Środowiska. Katedra Geologii Kopalnianej, Wydaw.
- Mucha J (2002) Struktura zmienności zawartości [Zn] i [Pb] w śląsko-krakowskich złożach Rud Zn-Pb. Polska Akademia Nauk – Kraków. Instytut Gospodarki Surowcami Mineralnymi i Energią. Studia Rozprawy Monografie.Wydawnictwo Instytutu Gospodarki Surowcami Mineralnymi i Energią IGSMiE PAN.
- Namyslowska-Wilczynska B (1993) Zmiennosc zloz rud miedzi na monoklinie przedsudeckiej w swietle badan geostatystycznych, Monografia, Warsaw, Poland.
- Namysłowska-Wilczyńska B (2006) Geostatystyka Teoria i Zastosowania. Monografia. Oficyna Wydawnicza Politechniki Wrocławskiej, Warsaw, Poland.
- Namyslowska-Wilczynska B (2012) Geostatistical methods used to estimate Sieroszowice copper ore deposit parameters. Journal for the Geological Sciences 40: 329-361.
- Namyslowska-Wilczynska B (2015) Application of turning bands technique to simulate values of copper ore deposit parameters in Rudna mine (Lubin-Sieroszowice region in SW part of Poland). Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards 9: 224-241.
- Namyslowska-Wilczynska B, Wilczyński A (2015) Geostatistical Characteristics of the Structure of Spatial Variation of Electrical Power in the National 110 KV Network Including Results of Variogram Model Components Filtering. Acta Energetica 1: 72-87.
- Namyslowska-Wilczynska B (2015) Geostatistical studies of space-temporal variation in selected quality parameters in Klodzko water supply system (SW part of Poland). J Geol Res Eng 3: 57-81.
- Namyslowska-Wilczynska B (2016) Space-Temporal Variation in Underground Water Some Quality Parameters in Klodzko Water Intake Area using Statistical and Geostatistical Methods (SW Part of Poland). J Geol Res Eng 4: 105-124.
- Namyslowska-Wilczynska B (2016) Geostatistical analysis of space variation in underground water various quality parameters in Klodzko water intake area (SW part of Poland). Studia Geotechnica et Mechanica 38: 15-34.
- Namysłowska-Wilczyńska B (2017) Filtrowanie składowych modeli wariogramów parametrów geologicznych złoża rud Cu, z zastosowaniem technik krigingowych. XL Zimowa Szkoła Mechaniki Górotworu i Geoinżynierii 61: 20-23.
- Namyslowska-Wilczynska B (2017) Filtration of components of Sieroszowice mine copper ore deposit variogram models by means of ordinary kriging technique, 18th Annual Conference IAMG2017, Fremantle-Perth, Australia.
- Namysłowska-Wilczyńska B, Wynalek J (2017) Geostatistical investigations of displacements on the basis of data from the geodetic monitoring of a hydrotechnical object. Studia Geotechnica et Mechanica, Proceedings of Hydrotechnics Problems Conference, Poland.
- Piotrowska A, Dlugosz J, Namyslowska-Wilczynska B, Zamorski R (2011) Field-scale variability of topsoil dehydrogenase and celluse activities as affected by variability of some physico-chemical properties. Biol Fertil Soils 47: 101-109.
- Chiles JP, Delfiner P (1999) Geostatistics, Modeling Spatial Uncertainty. Wiley Interscience, New York, USA.
- Rambert F (2005) Introduction to Mining Geostatistics, Geovariances Avon, France.
- Namyslowska-Wilczynska B (2013) Uncertainty estimation through geostatistical simulations, W: GEOMIN 2013, 3rd International Seminar on Geology for the Mining Industry, Santiago, Chile, USA.
- Geostatistics for Mining Engineers and Geologists (2015) Geovariances, Avon-Fontainebleau, France.
- Isatis (2015) Geostatistics Software for Improved Mining Resource Estimation Geovariances, Avon-Fontainebleau, France.
- Mucha J, Nieć M (1996) Struktura zmienności parametrów złoża [W:] Piestrzyński A. (red.) Monografia KGHM Polska Miedź SA, Lubin.
- Mucha J, Wasilewska M (2009) Trojwymiarowe modelowanie wartosci parametrow zlozowych metoda krigingu zwyczajnego 3D. Geologia/Akademia Gorniczo-Hutnicza im. Stanisława Staszica w Krakowie 35: 167-274.
- Isatis (2015) Software User’s Guide Ecole des Mines de Paris, Centre de Geostatistique, Fontainebleau, Geovariances, Avon Cedex, France.
- Isatis (2017) The latest edition of the Isatis manual, Geovariances, France.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi