Research Article, J Nanomater Mol Nanotechnol Vol: 12 Issue: 1
Influence of Arrhenius Activation Energy and Radiation Over the Flow of a Chemically Reacting Third Grade Hybrid Nanofluid on a Moving Flat Surface
Ogunsola AW, Ajala OA and Ajayi Tunde M*
Department of Mathematics, Ladoke Akintola University of Technology, Ogbomoso, Nigeria
*Corresponding Author: Ajayi Tunde M, Department of Mathematics
Ladoke Akintola University of Technology, Ogbomoso, Nigeria
E-mail: stillmetunde@gmail.com
Received date: 08 August, 2022, Manuscript No. JNMN-22-71853; Editor assigned date: 11 August, 2022, PreQC No. JNMN-22-71853 (PQ); Reviewed date: 25 August, 2022, QC No. JNMN-22-71853; Revised date: 06 January, 2023, Manuscript No. JNMN-22-71853 (R); Published date: 16 January, 2023, DOI: 10.4172/2324-8777.1000352
Citation: Ogunsola AW, Ajala OA, Ajayi Tunde M (2023) Influence of Arrhenius Activation Energy and Radiation Over the Flow of a Chemically Reacting Third Grade Hybrid Nanofluid on a Moving Flat Surface. J Nanomater Mol Nanotechnol 12:1.
Abstract
In this era of global quest for more energy, the hybrid nanofluid is a better choice compared to the conventional nanofluid. The intention here is to present the influence of both radiation and Arrhenius activation energy over a moving fluid. Similarity transformation is being employed to convert the governing equations of the problem to coupled ordinary differential equations and numerical solutions are obtained using MATLAB bvp5c. Effects of radiation, Arrhenius parameter, fluid parameter, Reynold number were examined, presented graphically and a discussion was made on same. It was noted that the hybrid nanofluid shows better result compared to nanofluid.
Keywords: Hybrid nanofluid, Moving plat, Third grade fluid, Radiation, Arrhenius activation energy
Keywords
Hybrid nanofluid; Moving plate; Third grade fluid; Radiation; Arrhenius activation energy
Introduction
Fluid flow has numerous applications in many fields not limited to applications in oil extraction, engine cooling systems, blood flow in the body, drug targeting, cleaning of soil from containment, hydraulic machines, refrigerators and air conditioners, hydroelectric plants. The quest for advancement in almost every sphere of life has necessitated researchers and scientists to develop new ideas and inject these in modern equipment and devices used in the mechanical, electrical, day to day life and industries, such as air conditioners, refrigerators, heat exchangers, electronic cooling, car radiators, solar thermal, energy storage, hydraulics system and heat pipes [1]. Simple liquids like water, oil, etc. were earlier being used for heat conduction and transfer of heat but it has been realized that they have fallen below the recent world’s demand for energy due to their poor thermal conductivity. A major achievement in this quest to solve the energy problem was recorded in 1995 which can be linked to Choi [2]. His research and subsequent works on what is today known as nanofluid indicated that nanofluids comparatively shows more thermal capacity and efficiency for heat transfer rate than simple or convectional fluids [3]. Deliberated on enhancing thermal conductivity of fluids with nanoparticles. The potential benefits of nanofluid with copper nanophase materials were estimated and one of such benefits is the dramatic reductions in the heat exchanger pumping power. Thermal transport in nanofluids was explicitly analyzed by Eastman, et al. made a review of nanofluid thermal conductivity and their heat transfer enhancements based on available experimental results [4-6]. Examined the energy destruction of forced convective nanofluid through a duct with constant wall temperature. Thermal energy storage behavior of Cu/paraffin nanofluids PCMs was numerically simulated [7]. Entropy analysis of third order nanofluid flow on a porous sheet was considered [8]. The role of slip on a two phase flow of Newtonian nanofluid was investigated [9]. In this era of emerging technology, a new version of nanofluid called hybrid nanofluid has been developed. Unlike the nanofluid, the hybrid nanofluid is made up of more than one metallic nanoparticle. Research shows that the hybrid nanofluid exhibits a higher heat transfer rate and more efficiency than the conventional fluids and nanofluids [10]. Analyzed the properties of hybrid nanofluid and its heat transfer phenomenon. The importance of hybrid nanofluid over simple nanofluids was discussed by [11]. The impacts of magnetic dipole on hybrid nanofluid flow were examined by [12]. The flow of Cu-Al2O3 hybrid nanofluid over a moving permeable surface was described by [13]. The energy transference of a hybrid nano suspension within a heated chamber was simulated [14]. The word ‘activation energy’ was introduced by Svante Arrhenius in 1889 and this refers to the minimum energy required to start a chemical reaction. Activation energy is a non-negotiable idea in oil emulsions, food processing, geothermal reservoirs and chemical engineering. The use and limitations of the activation energy as a means of evaluating thresholds, excitation functions and tunneling processes were discussed [15,16]. Addressed the characterization of the stagnation point flow of Carreau fluid induced due to the stretching of a chemically reacting surface. The influence of Arrhenius activation energy on the heat and mass transfer of second grade nanofluid flow was analyzed [17]. Reported that the Arrhenius activation energy influences a rise in fluid concentration. The effects of activation energy and dual stratification on the MHD flow of Maxwell nanofluid was discussed [18]. Analyzed the influence of activation energy on MHD buoyancy induced nanofluid flow past a vertical surface in the presence of radiation and chemical reaction. The knowledge of radiative heat transfer mechanism is essential in the field of power generation, fossil fuel combustion, solar power technology, nuclear reactor cooling, etc. [19]. Investigated the effects of radiation heat transfer on the convective flow of nanofluid. The subject was investigated [20] for a boundary layer flow over a convective flat surface [21]. A micropolar fluid to inspect the concept [22]. Examined the radiation effects of a nanofluid flow in the company of chemical reaction and activation energy.
Materials and Methods
Motivated by all the above works, here we have attempted a mathematical investigation on the influence of Arrhenius activation energy and radiation on the forced convection flow of a chemically reacting third grade hybrid nanofluid with temperature dependent fluid properties. To the best of our knowledge, these combined effects on a third grade hybrid nanofluid were not carried out in the past. Using similarity transformations, the governing equations are transformed into a system of ordinary differential equations. These obtained equations are solved numerically using matlab bvp5c. The results obtained are presented in tables and graphs and discussions thereafter made.
Nomenclature
B: Magnetic field strength
C: Concentration
Cp: Heat capacity at constant Pressure
Cw: Concentration at the wall
C∞: Concentration at the free stream
DB: Brownian diffusion coefficient
DT: Thermophoretic diffusion coefficient
Ea: Activation energy
k: Fluid thermal conductivity
k0: Universal gas constant
kr: Chemical reaction rate
n: Rate constant
P: Permeability of porous medium
T: Fluid Temperature
Tw, T∞: Temperature at the wall, ambient temperature
U0: Velocity stretching rate
u: Component of velocity in x direction
ue: Free stream velocity
uw: Velocity of the moving plate
v: Component of velocity in y direction
vw: Velocity normal to the plate (vw>0 signifies injection)
β3: Material fluid parameters
δ: Velocity parameter
ϑ: kinematic viscosity
ρnf: Nanofluid density
ρs: Density of nanosolid
μ: Fluid viscosity
μnf: Nanofluid viscosity
σ: Electrical conductivity of the fluid
ψ: Stream function
τ=(ρCρ)hnf/(ρCρ)f: Heat capacity ratio of nanoparticles to base fluid
ω: Nanoparticle volume fraction
Mathematical formulation
Consider a two dimensional, steady, boundary layer flow of a hybrid nanofluid made up of Ag/Au nanoparticles with third grade base fluid past a half infinite plate moving in a uniformly free flow, U as shown in Figure 2. The system is such that the x-axis is aligned to the plate surface while the y-axis is the coordinate measured normal to the plate. The hybrid nanofluid is taken to be in thermal equilibrium with no slip condition. In addition, the ambient fluid velocity of the plate is considered to be uw= δUx where δ is the parameter for plate velocity [23]. The hybrid nanofluids thermo physical characteristics are written in Figure 1.
Figure 1: Flow configuration of the model.
Figure 2: Variation in fluid parameter with velocity.
Based on the above assumptions together with ideas from previous works [24,25], the governing equations for the flow takes the form:
Where the component of velocity for and x axes y are u and v respectively, ue stands for the free stream velocity δ is the parameter for plate velocity. Furthermore, the density of hybrid nanofluid, ρhnf, viscosity of hybrid nanofluid, μhnf, heat capacity of hybrid nanofluid (ρCρ)hnf thermal conductivity of hybrid nanofluid Khnf, are as follow [26,27].
Where ρs1,ω1, (ρCρ)s1, ks1 the thermophysical properties for gold nanoparticle are, ρs2,ω1, (ρCρ)s2, ks2 are the thermophysical properties for silver nanoparticle, ρf, μf, (ρCp)f, kf are the thermophysical properties for the base fluid (Table 1).
| Material | Density (kg/m^3) | Specific Heat Capacity Cp (J/KgK) | Electrical Conductivity σ×10^(-5) (S/m) | Thermal Conductivity K(W/mk) |
|---|---|---|---|---|
| Aluminium Oxide (Al2O3) | 3970 | 765 | 0.85 | 40 |
| Blood | 1050 | 3617 | 0.18 | 0.52 |
| Copper (Cu) | 8933 | 385 | 1.67 | 401 |
| Gold (Au) | 19300 | 129 | 4.1 | 318 |
| Silver (Ag) | 10500 | 235 | 18.9 | 429 |
Table 1: Thermo physical properties of some nanofluids.
The Roseland approximation for radiation [28]:
Using Taylor’s series and neglecting higher order terms for the expansion of T4 about T∞ we finally have the radiation term in equation (3) to be
Introducing the established similarity variables and stream function Ψ used by Shehzard, Mohammed as
In this study, the fluid viscosity and thermal conductivity are assumed to be linear function of temperature in the form
Using equations (1-5) and variables (6-10), the continuity equation (1) is automatically satisfied and the governing equations reduced to the following ordinary differential equations [29,30]:
Where the parameters for third grade fluid β3=α3U02/pv, chemical reaction parameter Cr=kr2/U0, activation energy parameter E1=Ea/ k0T∞, Local magnetic parameter Hα=σhnfB2/ρhnfU0, Local Reynold number Φ=U0x2/v, Temperature dependent thermal conductivity parameter ∈=γ(Tw-T∞), Temperature dependent viscosity parameter ξ=b(Tw-T∞), Lewis number Le=v/DR, Brownian motion parameter Nb=DB/vT∞(Cw-C∞), Thermophoretic parameter Nt=DT/vT∞(Tw-T∞), Prandtl number Pr=(ρCp)fθ/kf, Radiation parameter Ra=kfk1/4σ2T∞3 , temperature difference parameter Td=(Tw-T∞)/T∞, The physical qualities of engineering interest in this study are the skin friction coefficient Cf, local Nusselt number Nuf and Sherwood number Sh which are defined as
Numerical solution
The coupled ordinary differential equations (11-13) and their corresponding boundary conditions (14) are first reduced to a system of first order equations using the method of superimposition [31]. This system of equations is thereafter solved numerically using the Matlab bvp5c solver.
Results and Discussion
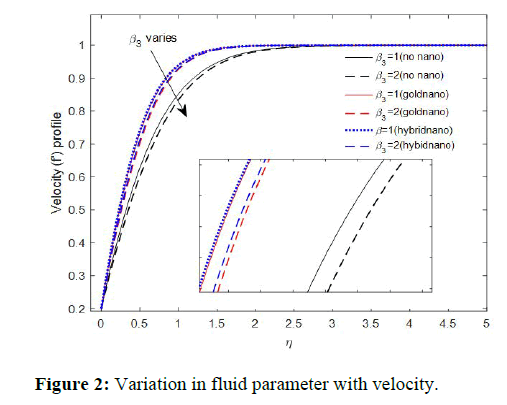
In order to analyze our results, numerical computation has been carried out for various values of Brownian motion parameter (Nb), Darcy number (Da) Forchheimer number (Fs), Hartmann number (Ha), Fluid material parameter (β3), Lewis number (Le), Prandtl number (Pr), Thermal conductivity parameter (∈ ), Thermophoretic parameter (Nt) and Velocity parameter (ε), using the numerical scheme discussed in the previous section. The numerical values obtained from the result are plotted in Figures 2-12 and Table 2. The influence of fluid parameter on fluid velocity was depicted in Figure 2.
It was observed that the fluid parameter reduces fluid motion. The Physics behind this is that increasing the fluid parameter decreases the stress that increases the value of the dynamic viscosity thereby producing fluid retardation. The variation in velocity with respect to local Reynold number was graphically illustration in Figure 3.
| ε | Pr | φ1 | β3 | f"(0) | -θ′(0) | -φ′(0) |
|---|---|---|---|---|---|---|
| 0.3 | 0.7 | 1 | 0.1 | -0.919171632869 | 3.371615 | 0.372866 |
| 0.5 | -0.919171632869 | 3.384494 | 0.372866 | |||
| 0.7 | -0.919171643828 | 3.393485 | 0.372866 | |||
| 0.7 | 0.6 | 1 | 0.1 | -0.919171643828 | 0.293713 | 3.397298 |
| 0.8 | -0.919171643828 | 0.336425 | 3.389693 | |||
| 1 | -0.919171643828 | 0.373302 | 3.3822 | |||
| 0.7 | 0.7 | 1 | 0.1 | -0.469620427220 | 0.320053 | 0.154215 |
| -1.237028774901 | 0.293558 | 3.10958 | ||||
| - 0.919171643828 | 0.315945 | 3.393485 | ||||
| 0.7 | 0.7 | 3 | 0.1 | -0.791743710779 | 0.31021 | 3.379875 |
| 5 | -0.725581578956 | 0.305244 | 3.372605 | |||
| 7 | -0.681583078104 | 0.300736 | 3.367966 | |||
| 0.7 | 0.7 | 1 | 0 | -1.079721786205 | 0.319372 | 3.407922 |
| 0.2 | -0.956916721305 | 0.317026 | 3.397209 | |||
| 0.4 | -0.888882527640 | 0.314909 | 3.390374 |
Table 2: Numerical results for different values of the controlling parameters and corresponding local skin friction, nusselt number and the local sherwood number.
Figure 3: Variation in reynold number (ϕ1) with velocity.
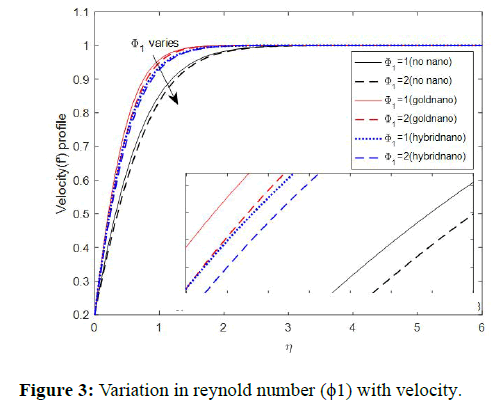
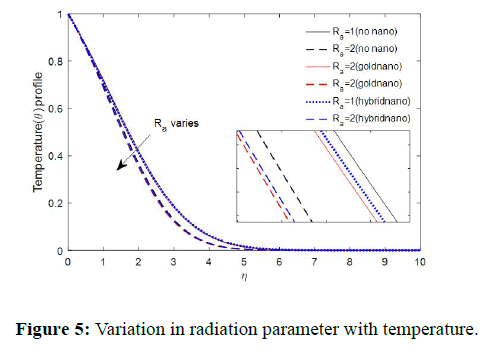
The figure showed that velocity profile reduces for an increase in local Reynold number. The reason for this boils from the fact that the local Reynold number given as ϕ1=U0X2/v is a function of the free stream velocity and plastic velocity. Hence, the two parameters acts to repel fluid flow which led to the decrease observed in fluid velocity as local Reynold increases. The effect of radiation parameter on the velocity profile is illustrated in Figure 4.
Figure 4: Variation in radiation parameter with velocity.
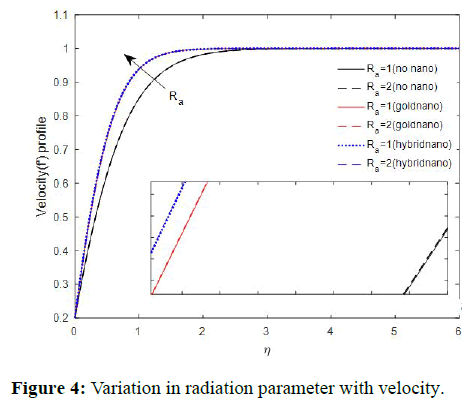
The figure revealed that radiation slightly increases fluid flow. This is in good agreement with Figure 5 reported Makinde and Olanrewaju [32]. On the other hand, a decrease in temperature was observed for an increase in the value of the radiation parameter as demonstrated in Figure 6.
Figure 5: Variation in radiation parameter with temperature.
Figure 6: Variation in thermal conductivity parameter (ϵ) with temperature.
The reason for this decrease in temperature is because large values of radiation parameter correspond to an increase in dominance of conduction over radiation, thus decreasing the thickness of the thermal boundary layer and increasing the heat loss to the ambient. Similar decrease in temperature due to increase in radiation parameter was reported in Figure 7 by Makinde and Olanrewaju [33] and Figure 8 by Zaib, et al. [34].
Figure 7: Variation in chemical reaction parameter (Cr) with concentration.
Figure 8: Variation in thermophoretic parameter (Nt) with concentration.
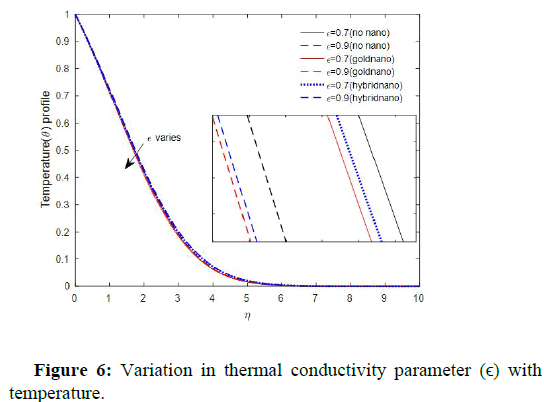
Figure 9 illuminates the variation in temperature caused by a change in thermal conductivity parameter. The figure revealed that temperature decreases as thermal conductivity parameter increases.
This observation is in harmony with reported by Hazarika and Konch Jadav. The influence of chemical reaction parameter on fluid concentration is graphically represented Figure 10.
Figure 9: Variation in arrhenius energy parameter (E1) with temperature.
Figure 10: Variation in arrhenius energy parameter (E1) with concentration.
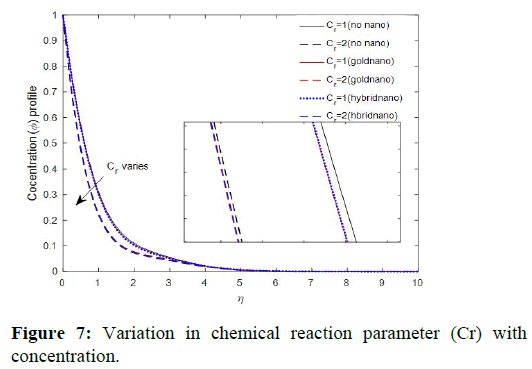
The Figure revealed that chemical reaction parameter suppresses fluid concentration. The physical significance of this, is that the number of solute molecules undergoing chemical reaction gets increased as chemical reaction parameter increases whereas other parameters (conditions) are constant, this therefore result in decrease in the concentration profile. This is in good agreement with reported by Makinde and Olanrewaju (Figure 11).
Figure 11: Variation in temperature difference parameter (Td) with temperature.
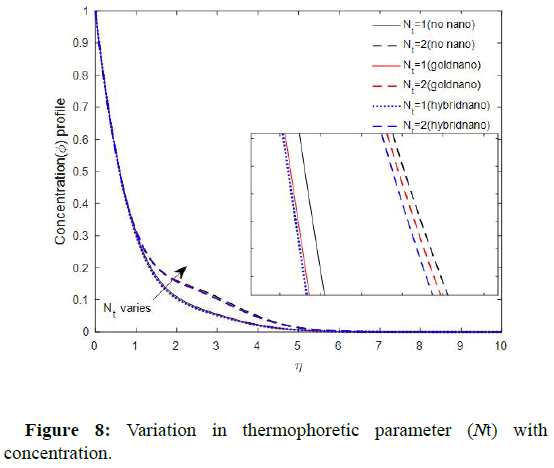
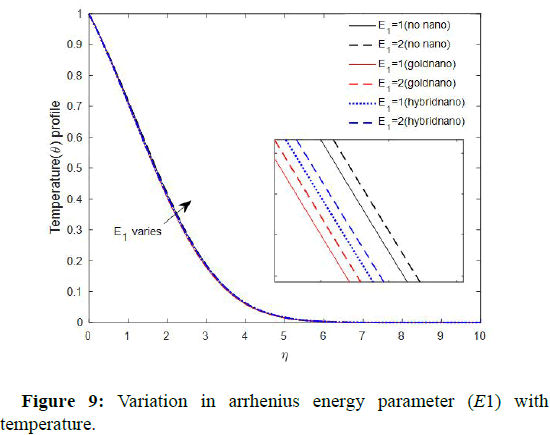
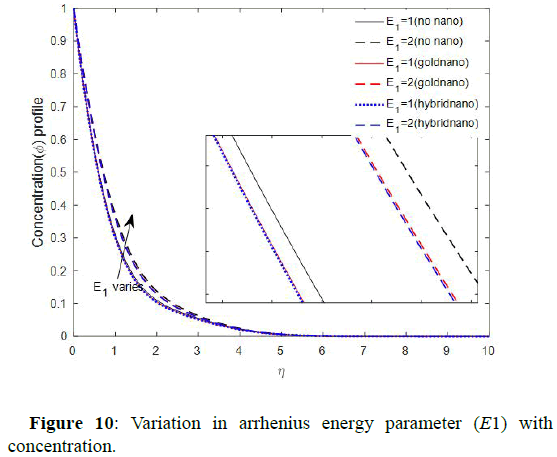
The variation of thermosphere tic parameter with concentration is elucidated. The figure shows that the concentration field is an increasing function of thermophoresis parameter. This observation is in good harmony with reported in Shehzad, et al. The influence of activation energy parameter on temperature is elucidated. The figure showed that activation energy increases fluid temperature. Showed the impact of activation energy on fluid concentration.
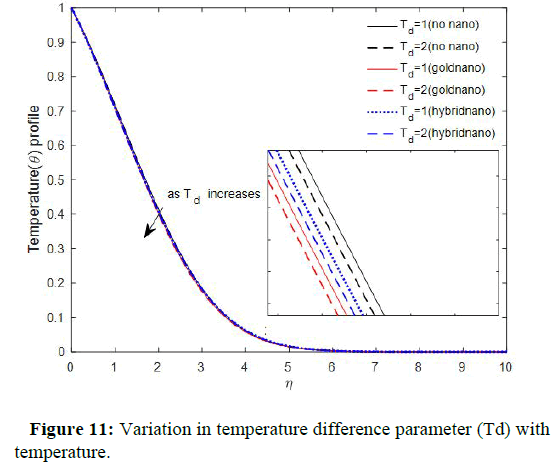
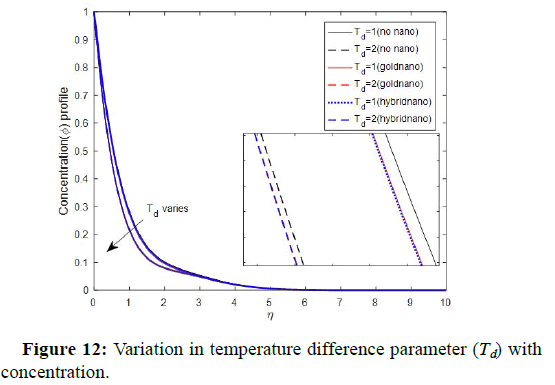
The figure elucidated that activation energy enhances the concentration profile. The Physics behind this is that a higher energy activation and weaker temperature leads to lower rate of reaction, which results in a slowdown in the chemical reaction and thus fluid concentration increases. This is in good agreement. This portrayed the influence of temperature difference parameter on fluid temperature. The figures showed that temperature difference reduce fluid temperature. The variation of temperature difference parameter with the fluid concentration is demonstrated in Figure 12. The figure revealed that temperature difference deflates the fluid concentration profile. This observation is in harmony with Figure 12 reported by Kiran Kumar, et al.
Figure 12: Variation in temperature difference parameter (Td) with concentration.
The effect of various parameters on the local skin friction, Nusselt number and Sherwood number is depicted in Table 2. The thermal conductivity parameter (ε) causes a negligible decrease in skin friction but increases the Nusselt number. Prandtl number has no effect on skin friction. Viscoelastic third grade parameter (β3) reduces the Nusselt number. The Nusselt number is an increasing function of the Prandtl number. However, viscoelastic third grade parameter (β3) reduces the Sherwood number.
Conclusion
The analysis of various parameters on steady laminar flow of an incompressible, electrically conducting non Newtonian hybrid nanofluid over a moving plate has been carried out. The following were detected: The fluid motion decreases on increasing the fluid parameter and Reynold number while the radiation parameter increases fluid motion.
• Fluid temperature decreases on increasing thermal conductivity, temperature difference and radiation parameters but Arrhenius energy parameter raises fluid temperature.
• The arrhenius energy and thermophoretic parameters increase the concentration of the fluid while the chemical reaction and temperature difference parameters reduce the fluid concentration profile.
• Thermal conductivity parameter and the Prandtl number because a rise in the Nusselt number but the material fluid parameter reduces it.
References
- AbdEl Galed SM, Hamad MAA (2013) MHD forced convection laminar boundary layer flow of alumina water nanofluid over a moving permeable flat plate with convective surface boundary condition. J Appl Math 1-8.
- Aladdin NAL, Bachok N, Pop I (2020) Cu-Al2O3/water hybrid nanofluid flow over a permeable moving surface in presence of hydromagnetic and suction effects. Alex Eng J 59:657-666.
- Animasaun IL (2015) Effects of thermophoresis, variable viscosity and thermal conductivity on free convective heat and mass transfer of anon-darcian MHD dissipative Casson fluid flow with nth order chemical reaction. J Niger Math Soc 34:11-31.
- Azam M, Xu T, Shakoor A, Khan M (1995) Effects of Arrhenius activation energy in development of covalent bonding in axisymmetric flow of radiative cross nanofluid. Int Commun Heat Mass Transf 113:104547.
- Choi SUS, Eastman JA (1995) Enhancing thermal conductivity of fluids with nanoparticles. Argonne National Lab.
- Eastman JA, Phillpot SR, Choi SUS, Keblinski P (2004) Thermal transport in nanofluids. Annu Rev Mater Res 34:219-246.
- Ellahi R, Hussain F, Asad Abbas S, Sarafraz MM, Goodarzi M, et al. (2020) Study of two phase newtonian nanofluid flow hybrid with hafnium particles under the effects of slip. Inventions 5:6.
- Fatunmbi EO, Adeniyan A (2020) Nonlinear thermal radiation and entropy generation on steady flow of magneto-micropolar fluid passing a stretching sheet with variable properties. Res Eng 6:100142.
- Gul T, Bilal M, Khan A, Aedh Alreshidi N, Mukhtar S et al. (2020) Magnetic dipole impact on hybrid nanofluid flow over an extending surface. Sci Rep 10:8474.
[Crossref] [Google Scholar] [PubMed]
- Hayat T, Nadeem S (2017) Heat transfer enhancement with Ag-CuO/water hybrid nanofluid. Results Phys 7:2317-2324.
- Hazarika GC, Konch Jadav (2014) Effects of variable viscosity and thermal conductivity on MHD free convective flow along a vertical porous plate with viscous dissipation. Int J Math Trends Technol 15:70-84.
- Jawad M, Saeed A, Tassaddiq A, Khan A, Gul T, et al. (2021) Insight into the dynamics of second grade hybrid radiative nanofluid flow with the boundary layer subject to lorentz force. Sci Rep 11:4894.
[Crossref] [Google Scholar] [PubMed]
- Jha BK, Samaila G (2020) Thermal radiation effect on boundary layer over a flat plate having convective surface boundary condition. SN Appl Sci 2:381.
- Kalaivanan R, Ganesh NV, Al-Mdallal QM (2020) An investigation on Arrhenius activation energy of second grade nanofluid flow with active and passive control of nanomaterials. Case Stud Therm Eng 22:100774.
- Kiran Kumar RVMSS, Vinod Kumar G, Raju CSK, Shehzad SA, Varma SVK, et al. (2018) Analysis of arrhenius activation energy in magnetohydrodynamic carreau fluid flow through improved theory of heat diffusion and binary chemical reaction. J Phys Commun 2:035004.
- Lakshmi Devi G, Niranjan h, Sivasankaran S (2022) Effects of chemical reactions radiation and activation energy on MHD buoyancy induced nanofluid flow past a vertical surface. Scientia Iranica 29:90-100.
- Loganathan K, Muhiuddin G, Alanazi AM, Fehaid S, Alshammari Bader M, et al. (2020) Entropy optimization of third-grade nanofluid slip flow embedded in a porous sheet with zero mass flux and a non-fourier heat flux. Model Front Phys 8:250.
- Mahanthesh B, Gireesha BJ, Gorla RS (2016) Heat and mass transfer effects on the mixed convective flow of chemically reacting nanofluid past a moving/stationary vertical plate. Alexandria Eng J 55:569-581.
- Majeed A, Noori FM, Zeeshan A, Mahmood T, Rehman SU, et al. (2018) Analysis of activation energy in magnetohydrodynamic flow with chemical reaction and second order momentum slip model. Case Stud Therm Eng 12:765-773.
- Makinde OD, Olanrewaju PO (2011) Unsteady mixed convection with soret and dufour effects past a porous plate moving through a binary mixture of chemically reacting fluid. Chem Eng Commun 198:920-938.
- Mekheimer KhS, Hasona WM, Abo-Elkhair RE, Zaher AZ (2018) Peristaltic blood flow with gold nanoparticles as a third grade nanofluid in catheter: Application of cancer therapy. Phys Lett A 382:85-93
- Menzinger M, Wolfgang RL (1969) The meaning and use of the arrhenius activation energy. Angew Chem Int Ed 8:438-444.
- Mustafa M, Mushtaq A, Hayat T, Ahmad B (2014) Nonlinear radiation heat transfer effects in the natural convective boundary layer flow of nanofluid past a vertical plate: A numerical study. PLoS One 9:e103946.
[Crossref] [Google Scholar] [PubMed]
- Na TY (1979) Computational methods in engineering boundary value problems.
- Nadeem S, Abbas N, Khan AU (2018) Characteristics of three dimensional stagnation point flow of hybrid nanofluid past a circular cylinder. Results phys 8:829-835.
- Prasad KV, Vajravelu K, Datti PS (2010) The effects of variable fluid properties on the hydromagnetic flow and heat transfer over a non linearly stretching sheet. Int J Ther Sci 49:603-610.
- Rashidi MM, Sadri M, Sheremet MA (2021) Numerical simulation of hybrid nanofluid mixed convection in a lid driven square cavity with magnetic field using high-order compact scheme. Nanomaterials 11:2250.
[Crossref] [Google Scholar] [PubMed]
- Rezaee FK, Tayebi A (2010) Exergy destruction of forced convective (ethylene glycol+alumina) nanofluid through a duct with constant wall temperature in contrast to (ethylene glycol) fluid. J Appl Sci 10:1279-1285.
- Sandhya G, Sreelakshmi K, Sarojamma G (2020) Effect of arrhenius activation energy and dual stratifications on the MHD flow of a maxwell nanofluid with viscous heating. Int J Eng Sci 1805:55-60.
- Shehzad SA, Hussain Tariq, Hayat T, Ramzan M, Alsaedi A (2015) Boundary layer flow of third grade nanofluid with Newtonian heating and viscous dissipation. J Cent South Univ 22:360-367.
- Shuying Wu, Hua Wang, Song Xiao, Dongsheng Zhu (2012) Numerical simulation on thermal energy stored behavior of Cu/paraffin nanofluids PCMs. Procedia Eng 31:240-244.
- Suresh S, Venkitaraj KP, Selvakumar P, Chandrasekar M (2012) Effect of Al2O3-Cu/water hybrid nanofluid in heat transfer. Exp Therm Fluid Sci 38:54-60.
- Yu W, France DM, Routbort JL, Choi SUS (2008) Review and comparison of nanofluid thermal conductivity and heat transfer enhancements. Heat Transf Eng 29:432-460.
- Zaib A, Chamkha AJ, Rashidi MM, Bhattacharyya K (2018) Impact of nanoparticles on flow of a special non-Newtonian third grade fluid over a porous heated shrinking sheet with nonlinear radiation. Nonlinear Engineering 7:103-111.
