Research Article, J Nucl Ene Sci Power Generat Technol Vol: 8 Issue: 2
Investigation of Shielding Parameters for Barite and Boron Carbide Polymer Composite
1Jouf University, Departm ent of Physics, Post Office 207, Al Jouf, Saudi Arabia
2Laboratories for Detection of Landmines and Illicit Materials, Nuclear Research Centre, Atomic Energy Authority, Cairo, Egypt
*Corresponding AM Osman
Jouf University, Faculty of Science and Arts at Tabarjal, Department of Physics, Post Office 207, Al Jouf, Saudi Arabia.
E-mail: amoa@ju.edu.sa.
Received: August 26, 2019 Accepted: September 23, 2019 Published: September 30, 2019
Citation: Sman AM (2019) Investigation of Shielding Parameters for Barite and Boron Carbide Polymer Composite. J Nucl Ene Sci Power Generat Technol 8:2.
Abstract
In this study, the shielding parameters for Glycidyl methacrylate with different ratio of Barite and Boron Carbide Polymer composites were theoretically calculated. The mass attenuation coefficients have been calculated at the photon energy range of 1 keV-1 GeV by using XCom program. The obtained data will be used to
calculate the effective atomic number (Zeff) and effective electron density (Neff) for the same range of energy. The macroscopic fast neutron removal cross-sections have also been calculated. The dependence of mass attenuation coefficients and the macroscopic fast neutron removal cross-sections on chemical composition of
the selected polymer composites have been discussed. Also, the dependence of characteristics gamma-ray shielding parameters for the composite on incident photon energy has been studied. Barite shows up as good attenuating material, while Boron samples are relatively weak gamma-ray attenuators. The effect of the compound composition appears obviously in this study. As well as, the obtained results through this study can be utilized to comprehend the shielding effectiveness of this composite.
Keywords: Barite; Boron carbide; Polymer composite; Effective atomic number; Effective electron density; Fast neutron removal cross-sections 1
Introduction
Due to the increasing nuclear applications in different fields makes nuclear radiation to play an important role in our daily life. Various beneficial applications of different types of radiations are in the field of medicine, industry, agriculture, and research. Neutron and gamma-ray sources are not only dangerous to human being but also to sensitive laboratory equipment’s. Radiation shielding is necessary to protect penetrative neutrons and gamma-rays. The intensity of penetrating radiation such as neutrons and gamma-rays is varied by three factors: time, distance and shielding. The most effective method for attenuation of radiation is shielding [1]. Filler-reinforced polymers have gained increasing attention from X-ray technologists in radiation shielding since polymers have great potential in many important applications by virtue of their unique properties, such as low density, the ability to form intricate shapes, optical transparency, low manufacturing cost, and toughness. One of the filler-reinforced polymers commonly used for radiation shielding is lead acrylic. Moreover, some researchers have also tried to synthesize nano-sized filler-reinforced polymers for radiation shielding by virtue of the size effect in X-ray attenuation [2-4].
The mass attenuation coefficient, μ/ρ, is a measure of the average number of interactions between incident photons and matter that occur in a given mass-per-unit area thickness of the material encountered [5]. Accurate values of the mass attenuation coefficient, μ/ρ, are required in the nuclear diagnostics, radiation protection, nuclear medicine, radiation biophysics, radiation dosimetry to obtain essential data. The mass attenuation coefficients are also used to determine photon penetration and energy deposition in the biological and other materials [6-8]. The mass attenuation coefficients can be obtained from different database [9] and XCom program [10]. Because of photon interaction cross-section for elements of the composite material, a single atomic number is a characteristic of element will not describe the atomic number of composite material in all energy ranges. So a new number for composite materials is called to be effective atomic number, Zeff, suggested by [9] and it varies with energy. Determination of the effective atomic number, Zeff, and the effective electron number per unit mass, Neff, which is another important parameter for composite materials is very important in the fields of many technological applications and nuclear medicine for the calculation of dose in radiation therapy and medical imaging [6,11].
Neutron penetration in shielding is characterized by several parameters such as the effective removal cross-sections, the macroscopic thermal neutron cross-section. Effective removal cross-section, ΣR (cm2/g) is a measure of the probability that fast or fission energy neutron undergoes a first collision, which removes it from the group of the penetrative un-collided neutrons [12,13]. It is approximately constant for neutron energies between 2 and 12 MeV. The concept of ΣR is used as long as the shielding material under investigation contains some scattering nuclides. However, when there are no scattering nuclides around the beam another quantity, the total mass neutron cross-section ΣT (cm2/g), is used. Observed values of the ΣR are roughly 2/3 of ΣT for neutrons of energies in the range from 6 to 8 MeV [14-17].
In this work, the total mass attenuation coefficient (μm) has been determined theoretically by using XCom code at energies from 1 keV to 1 GeV. Since the effective atomic number, Zeff, and the effective electron number per unit mass, Neff, are widespread use; this study is focusing on calculating the effective atomic number and effective electron density of polymer composites with different barite and boron carbide percentages. Also, the effective removal cross-section has been calculated theoretically by using the values of removal crosssection of elements which constitute the polymer composition. The elemental composition for the Glycidyl methacrylate with different ratio of Barite and Boron Carbide Composite are displayed in Table 1.
| Element | Fraction by weight | ||||||
|---|---|---|---|---|---|---|---|
| Barite 0% | Barite 5% | Barite 10% | Barite 15% | Barite 20% | Barite 25% | Barite 30% | |
| (P1) | (PB2) | (PB3) | (PB4) | (PB5) | (PB6) | (PB7) | |
| ρ=1.07 g/cm3 | ρ=1.24g/cm3 | ρ=1.41g/cm3 | ρ=1.58 g/cm3 | ρ=1.75 g/cm3 | ρ=1.92 g/cm3 | ρ=2.09 g/cm3 | |
| H | 0.070904 | 0.067359 | 0.063814 | 0.060268 | 0.056723 | 0.053178 | 0.049633 |
| C | 0.591448 | 0.561876 | 0.532303 | 0.502731 | 0.473158 | 0.443586 | 0.414014 |
| O | 0.337648 | 0.334476 | 0.331304 | 0.328132 | 0.32496 | 0.321788 | 0.318616 |
| S | 0 | 0.00687 | 0.013739 | 0.020609 | 0.027478 | 0.034348 | 0.041218 |
| Ba | 0 | 0.02942 | 0.05884 | 0.08826 | 0.11768 | 0.1471 | 0.17652 |
| Element | Boron carbide 0% |
Boron carbide 5% |
Boron carbide 10% |
Boron carbide 15% |
Boron carbide 20% |
Boron carbide 25% |
Boron carbide 30% |
| (P1) | (PBC2) | ( PBC3) | (PBC4) | (PBC5) | (PBC6) | (PBC7) | |
| ρ=1.07 g/cm3 | ρ=1.14 g/cm3 | ρ=1.21 g/cm3 | ρ=1.28 g/cm3 | ρ=1.36 g/cm3 | ρ=1.43 g/cm3 | ρ=1.50 g/cm3 | |
| H | 0.070904 | 0.067359 | 0.063814 | 0.060268 | 0.056723 | 0.053178 | 0.049633 |
| B | 0 | 0.039131 | 0.078263 | 0.117394 | 0.156525 | 0.195657 | 0.234788 |
| C | 0.591448 | 0.572744 | 0.554041 | 0.535337 | 0.516633 | 0.497929 | 0.479226 |
| O | 0.337648 | 0.320766 | 0.303883 | 0.287001 | 0.270118 | 0.253236 | 0.236354 |
| Element | Barites 0% | Barite 2.5% | Barite 5% | Barite 7.5% | Barite 10% | Barite 12.5% | Barite 15% |
| Boron carbide 0% |
Boron carbide 2.5% |
Boron carbide 5% |
Boron carbide 7.5% |
Boron carbide 10% |
Boron carbide 12.5% |
Boron carbide 15% |
|
| (P1) | (PBBC2) | (PBBC3) | (PBBC4) | (PBBC5) | (PBBC6) | (PBBC7) | |
| ρ=1.07 g/cm3 | ρ=1.19 g/cm3 | ρ=1.13 g/cm3 | ρ=1.43 g/cm3 | ρ=1.55 g/cm3 | ρ=1.67 g/cm3 | ρ=1.79 g/cm3 | |
| H | 0.070904 | 0.067359 | 0.063814 | 0.060268 | 0.056723 | 0.053178 | 0.049633 |
| B | 0 | 0.019566 | 0.039131 | 0.058697 | 0.078263 | 0.097828 | 0.117394 |
| C | 0.591448 | 0.56731 | 0.543172 | 0.519034 | 0.494896 | 0.470758 | 0.44662 |
| O | 0.337648 | 0.327621 | 0.317594 | 0.307566 | 0.297539 | 0.287512 | 0.277485 |
| S | 0 | 0.003435 | 0.00687 | 0.010304 | 0.013739 | 0.017174 | 0.020609 |
| Ba | 0 | 0.01471 | 0.02942 | 0.04413 | 0.05884 | 0.07355 | 0.08826 |
Table 1: Abbreviation and elemental composition and density for glycidyl methacrylate with different ratio of barite and boron carbide composite.
Methodology of Calculations
Gamma-ray and neutron radiation shielding parameters for Barite and Boron Carbide Polymer composites were theoretically calculated as following:
Gamma-ray calculations
When a gamma-ray passes through a matter, its intensity progressively reduces as a consequence of interactions between photons and atoms. The mass attenuation coefficient μ/ρ, (cm2/g) is a measure of the average number of interactions that occur between photons and matter.
Consider first a chemical compound. The formulas will later be generalized to mixtures as well. The total photon interaction crosssection, σm, per molecule can be written as follows:
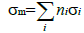(1)
Where ni is the number of atoms of the ith constituent element, and σi is total photon interaction cross-section per atom of element i. The total number, n, of atoms in the molecule is
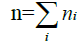(2)
Suppose that the cross-section per molecule can be written in terms of an effective (average) cross-section, σa, per atom and an effective cross-section, σe, per electron as follows:
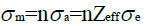(3)
From the first equality of Eq. (3) the effective cross-section per atom is given by:
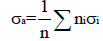(4)
In the same way, the effective cross-section per electron is given by:
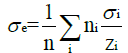(5)
It follows from the last equality of Eq. (3) that the effective atomic number can be written as:
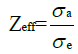(6)
By inserting the expressions (4) and (5) for σa and σe:
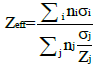(7)
For a chemical compound one has
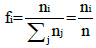(8)
Where Σi fi= 1 Rewriting Eq. (7) in terms of molar, fractions give the more general expression
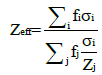(9)
Eq. (9) is then the basic relation for calculating the effective atomic number for all types of materials, compounds as well as mixtures.
The atomic cross-section, σi, of the ith constituent element, is related to the corresponding mass attenuation coefficient, (μ/ρ)i, through the relation:
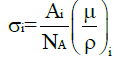(10)
Where Ai is the atomic mass and NA is the Avogadro constant. Useful expressions in terms of the mass attenuation coefficient can be obtained by inserting expression (10) for σi in the equations of the previous section.
Consider first a chemical compound. Inserting the expression (10) for σi in Eq. (7) gives the following relation for Zeff:
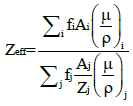(11)
Eq. (11) can be used for calculating the effective atomic number of both compounds and mixtures.
The effective atomic number, Zeff, is closely related to the electron density, Neff, which is expressed in a number of electrons per unit mass. For a chemical element, the electron density is given by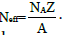 
This expression can be generalized to a compound, and one has
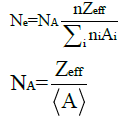(12)
Where A is the average atomic mass of the compound? It can be shown that the electron density also is given by
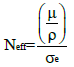(13)
Where μ/ρ is the total mass attenuation coefficient of the compound, and σe is the electronic cross-section given by Eq. (5). In the case of Compton scattering, the Klein-Nishina cross-section can be used for σe.
Fast neutron calculations
The interaction of neutrons with the atoms described by the total microscopic cross-section (σt), expresses the probability that a neutron of given energy interacts with the atoms of the traversed material and it is defined as the sum of the microscopic cross-section scattering (σs) and the microscopic cross-section absorption (σa).
σt=σs+σa (14)
The neutrons attenuation during their passage through a material medium depends not only on the microscopic cross-section but also on the number of nuclei within this environment. The physical quantity bounding these two parameters is called total macroscopic cross-section denoted (Σt) and defined by [18,19]:
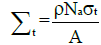(15)
Where (ρ) is the density (g/cm3), Na is Avogadro’s number and A is the atomic mass. In the same way as a photons beam, when the parallel beam of monoenergetic neutrons passes through a material medium, it will be attenuated due to absorption and scattering. The attenuation of neutrons in matter follows the following law:
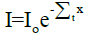(16)
where I0 and I are the incidents and transmitted intensities, x(cm) is the thickness of the material medium and Σt represents the total macroscopic cross-section.
So the case of fast neutron attenuation is described by another parameter called the removal cross-section, denoted by (ΣR) (cm-1) and is different from the total macroscopic cross-section but it has a fraction of it. The removal cross-section presents the probability that a fast or fission-energy neutron undergoes a first collision, which removes it from the group of penetrating un-collided neutrons.
For energies between 2 and 12 MeV, the effective removal crosssection will be almost constant when the traversed medium contains a large amount of hydrogen ΣR -Σt and when materials contain a small fraction of hydrogen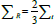 
for energy between 6 and 8 MeV. A material sample having as components: simple elements and compounds, its removal cross-section is given by the following formula [14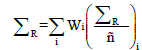-17]:
(17)
Where Wi, (ρ) and (ΣR/ρ)i are respectively the partial density (g/ cm3), density and mass removal cross-section of the ith constituent. The partial density of the ith constituent is given by:
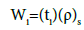(18)
Where (ti) is the weight fraction of the ith constituent and (ρ)s is the sample density.
In this study, the effective removal cross-section (ΣR) of fast neutrons has been calculated for polymer composites with different ratios of barite and boron carbide by using Eqn. 17. The values of the mass removal cross-sections of the elements that constitute of these materials are taken from [20,21].
Results and Discussion
In this study, the basic radiation parameters of polymer composites with different ratios of Barite and Boron Carbide were studies by the direct method over a wide photon energy range from 1 keV to 1 GeV using XCom program. These parameters are the μ/ρ, Zeff, Neff. As well as the effective removal cross-section (ΣR/ρ) of fast neutrons has been calculated for the investigated Samples.
The Zeff and Neff values of Polymer composites (equal proportions of barite and boron carbide) are given in Tables 2 and 3 only for total photon interaction. The tables present Zeff and Neff values in the energy range from 1 keV to 20 MeV, however, the values for the energy range from 1 keV to 1 GeV are displayed in graphical results. The elemental composition of materials used in this work, its fractions by weight and calculated (ΣR/ρ) values are listed in Table 4.
| Energy (MeV) | (PBBC1) | (PBBC2) | (PBBC3) | (PBBC4) | (PBBC5) | (PBBC6) | (PBBC7) |
|---|---|---|---|---|---|---|---|
| 1E-3 | 7.08 | 9.65 | 12.1 | 14.3 | 16.5 | 18.5 | 20.5 |
| 0.0015 | 7.11 | 13.8 | 19 | 23.3 | 26.9 | 29.9 | 32.4 |
| 0.002 | 7.13 | 19.4 | 27 | 32.2 | 36 | 38.8 | 41.1 |
| 0.003 | 7.16 | 34.3 | 42.3 | 46.1 | 48.3 | 49.8 | 50.8 |
| 0.004 | 7.17 | 42.1 | 47.4 | 49.5 | 50.7 | 51.4 | 51.9 |
| 0.005 | 7.18 | 47.1 | 50.6 | 52 | 52.7 | 53.1 | 53.4 |
| 0.006 | 7.18 | 50.8 | 53 | 53.8 | 54.3 | 54.5 | 54.7 |
| 0.008 | 7.18 | 53.3 | 54.5 | 54.9 | 55.1 | 55.2 | 55.3 |
| 0.01 | 7.17 | 54.4 | 55.1 | 55.3 | 55.4 | 55.5 | 55.5 |
| 0.015 | 7.07 | 55.5 | 55.7 | 55.8 | 55.8 | 55.8 | 55.8 |
| 0.02 | 6.91 | 55.6 | 55.8 | 55.8 | 55.8 | 55.9 | 55.9 |
| 0.03 | 6.62 | 55.7 | 55.8 | 55.9 | 55.9 | 55.9 | 55.9 |
| 0.04 | 6.46 | 55.3 | 55.6 | 55.7 | 55.8 | 55.8 | 55.8 |
| 0.05 | 6.39 | 54.8 | 55.4 | 55.6 | 55.7 | 55.8 | 55.8 |
| 0.06 | 6.36 | 54.1 | 55 | 55.4 | 55.5 | 55.6 | 55.7 |
| 0.08 | 6.33 | 54 | 55 | 55.3 | 55.5 | 55.6 | 55.7 |
| 0.1 | 6.32 | 55.3 | 55.7 | 55.8 | 55.8 | 55.9 | 55.9 |
| 0.15 | 6.32 | 55.4 | 55.7 | 55.8 | 55.8 | 55.9 | 55.9 |
| 0.2 | 6.32 | 55.4 | 55.7 | 55.8 | 55.8 | 55.9 | 55.9 |
| 0.3 | 6.32 | 55.6 | 55.8 | 55.9 | 55.9 | 55.9 | 55.9 |
| 0.4 | 6.32 | 55.6 | 55.8 | 55.9 | 55.9 | 55.9 | 55.9 |
| 0.5 | 6.32 | 55.6 | 55.8 | 55.9 | 55.9 | 55.9 | 55.9 |
| 0.6 | 6.32 | 55.7 | 55.8 | 55.9 | 55.9 | 55.9 | 56 |
| 0.8 | 6.32 | 55.7 | 55.9 | 55.9 | 55.9 | 55.9 | 56 |
| 1.0 | 6.32 | 55.5 | 55.7 | 55.8 | 55.9 | 55.9 | 55.9 |
| 1.022 | 6.32 | 55.1 | 55.5 | 55.7 | 55.8 | 55.8 | 55.9 |
| 1.25 | 6.32 | 53.6 | 54.8 | 55.2 | 55.4 | 55.5 | 55.6 |
| 1.5 | 6.32 | 51.4 | 53.6 | 54.4 | 54.8 | 55.1 | 55.2 |
| 2.0 | 6.32 | 45.5 | 50.2 | 52.1 | 53 | 53.6 | 54 |
| 2.044 | 6.32 | 39.7 | 46.4 | 49.2 | 50.8 | 51.8 | 52.5 |
| 3 | 6.33 | 52.8 | 54.4 | 54.9 | 55.2 | 55.4 | 55.5 |
| 4 | 6.35 | 52.8 | 54.4 | 54.9 | 55.2 | 55.4 | 55.5 |
| 5 | 6.36 | 51 | 53.4 | 54.3 | 54.7 | 55 | 55.2 |
| 6 | 6.37 | 49 | 52.3 | 53.5 | 54.1 | 54.5 | 54.8 |
| 7 | 6.38 | 43.6 | 49 | 51.2 | 52.3 | 53.1 | 53.6 |
| 8 | 6.4 | 38 | 45.1 | 48.3 | 50.1 | 51.2 | 52 |
| 9 | 6.41 | 25.8 | 34.5 | 39.4 | 42.6 | 44.8 | 46.4 |
| 10 | 6.42 | 19.1 | 26.8 | 32 | 35.7 | 38.5 | 40.6 |
| 11 | 6.43 | 13.5 | 19 | 23.3 | 26.8 | 29.7 | 32.2 |
| 12 | 6.44 | 11.6 | 15.9 | 19.6 | 22.7 | 25.4 | 27.8 |
| 13 | 6.45 | 10.8 | 14.5 | 17.7 | 20.6 | 23.1 | 25.4 |
| 14 | 6.46 | 10.3 | 13.7 | 16.7 | 19.3 | 21.7 | 23.9 |
| 15 | 6.47 | 9.69 | 12.6 | 15.2 | 17.7 | 19.8 | 21.9 |
| 16 | 6.48 | 9.35 | 12 | 14.4 | 16.6 | 18.7 | 20.6 |
| 18 | 6.49 | 9.41 | 12.1 | 14.5 | 16.8 | 18.9 | 20.8 |
| 20 | 6.5 | 9.18 | 11.7 | 13.9 | 16.1 | 18 | 19.9 |
Table 2: Effective atomic number of polymer composites for total photon interaction (with coherent).
| Energy (MeV) | (PBBC1) | (PBBC2) | (PBBC3) | (PBBC4) | (PBBC5) | (PBBC6) | (PBBC7) |
|---|---|---|---|---|---|---|---|
| 1E-3 | 6E23 | 1.27E24 | 1.58E24 | 1.88E24 | 2.16E24 | 2.43E24 | 2.68E24 |
| 0.0015 | 6.03E23 | 1.81E24 | 2.5E24 | 3.06E24 | 3.52E24 | 3.91E24 | 4.24E24 |
| 0.002 | 6.05E23 | 2.54E24 | 3.54E24 | 4.22E24 | 4.71E24 | 5.08E24 | 5.37E24 |
| 0.003 | 6.07E23 | 4.5E24 | 5.54E24 | 6.04E24 | 6.33E24 | 6.51E24 | 6.64E24 |
| 0.004 | 6.08E23 | 5.52E24 | 6.21E24 | 6.49E24 | 6.63E24 | 6.72E24 | 6.78E24 |
| 0.005 | 6.08E23 | 6.18E24 | 6.64E24 | 6.81E24 | 6.9E24 | 6.95E24 | 6.98E24 |
| 0.006 | 6.09E23 | 6.67E24 | 6.96E24 | 7.06E24 | 7.1E24 | 7.13E24 | 7.15E24 |
| 0.008 | 6.08E23 | 7E24 | 7.14E24 | 7.19E24 | 7.21E24 | 7.22E24 | 7.23E24 |
| 0.01 | 6.07E23 | 7.13E24 | 7.22E24 | 7.25E24 | 7.26E24 | 7.26E24 | 7.26E24 |
| 0.015 | 5.99E23 | 7.28E24 | 7.3E24 | 7.31E24 | 7.31E24 | 7.3E24 | 7.3E24 |
| 0.02 | 5.86E23 | 7.3E24 | 7.31E24 | 7.32E24 | 7.31E24 | 7.31E24 | 7.31E24 |
| 0.03 | 5.61E23 | 7.3E24 | 7.32E24 | 7.32E24 | 7.32E24 | 7.31E24 | 7.31E24 |
| 0.04 | 5.47E23 | 7.26E24 | 7.3E24 | 7.3E24 | 7.31E24 | 7.3E24 | 7.3E24 |
| 0.05 | 5.41E23 | 7.2E24 | 7.27E24 | 7.29E24 | 7.29E24 | 7.29E24 | 7.29E24 |
| 0.06 | 5.39E23 | 7.1E24 | 7.22E24 | 7.25E24 | 7.27E24 | 7.28E24 | 7.28E24 |
| 0.08 | 5.37E23 | 7.09E24 | 7.21E24 | 7.25E24 | 7.27E24 | 7.28E24 | 7.28E24 |
| 0.1 | 5.36E23 | 7.26E24 | 7.3E24 | 7.31E24 | 7.31E24 | 7.31E24 | 7.31E24 |
| 0.15 | 5.36E23 | 7.27E24 | 7.3E24 | 7.31E24 | 7.31E24 | 7.31E24 | 7.31E24 |
| 0.2 | 5.36E23 | 7.27E24 | 7.3E24 | 7.31E24 | 7.31E24 | 7.31E24 | 7.31E24 |
| 0.3 | 5.36E23 | 7.3E24 | 7.32E24 | 7.32E24 | 7.32E24 | 7.32E24 | 7.31E24 |
| 0.4 | 5.36E23 | 7.3E24 | 7.32E24 | 7.32E24 | 7.32E24 | 7.32E24 | 7.31E24 |
| 0.5 | 5.36E23 | 7.3E24 | 7.32E24 | 7.32E24 | 7.32E24 | 7.32E24 | 7.31E24 |
| 0.6 | 5.36E23 | 7.31E24 | 7.32E24 | 7.33E24 | 7.32E24 | 7.32E24 | 7.32E24 |
| 0.8 | 5.36E23 | 7.31E24 | 7.33E24 | 7.33E24 | 7.32E24 | 7.32E24 | 7.32E24 |
| 1 | 5.36E23 | 7.28E24 | 7.31E24 | 7.32E24 | 7.32E24 | 7.31E24 | 7.31E24 |
| 1.022 | 5.36E23 | 7.23E24 | 7.28E24 | 7.3E24 | 7.3E24 | 7.3E24 | 7.3E24 |
| 1.25 | 5.36E23 | 7.04E24 | 7.19E24 | 7.23E24 | 7.26E24 | 7.27E24 | 7.27E24 |
| 1.5 | 5.36E23 | 6.75E24 | 7.04E24 | 7.13E24 | 7.18E24 | 7.21E24 | 7.22E24 |
| 2 | 5.36E23 | 5.98E24 | 6.59E24 | 6.82E24 | 6.94E24 | 7.02E24 | 7.06E24 |
| 2.044 | 5.36E23 | 5.22E24 | 6.08E24 | 6.45E24 | 6.66E24 | 6.78E24 | 6.87E24 |
| 3 | 5.37E23 | 6.93E24 | 7.13E24 | 7.2E24 | 7.23E24 | 7.24E24 | 7.25E24 |
| 4 | 5.38E23 | 6.93E24 | 7.13E24 | 7.2E24 | 7.23E24 | 7.24E24 | 7.25E24 |
| 5 | 5.39E23 | 6.7E24 | 7.01E24 | 7.11E24 | 7.17E24 | 7.19E24 | 7.21E24 |
| 6 | 5.4E23 | 6.43E24 | 6.86E24 | 7.01E24 | 7.09E24 | 7.13E24 | 7.16E24 |
| 7 | 5.41E23 | 5.73E24 | 6.43E24 | 6.71E24 | 6.85E24 | 6.95E24 | 7.01E24 |
| 8 | 5.42E23 | 4.99E24 | 5.92E24 | 6.33E24 | 6.55E24 | 6.7E24 | 6.8E24 |
| 9 | 5.43E23 | 3.39E24 | 4.53E24 | 5.17E24 | 5.58E24 | 5.86E24 | 6.07E24 |
| 10 | 5.44E23 | 2.51E24 | 3.51E24 | 4.19E24 | 4.67E24 | 5.03E24 | 5.31E24 |
| 11 | 5.45E23 | 1.77E24 | 2.49E24 | 3.05E24 | 3.51E24 | 3.89E24 | 4.21E24 |
| 12 | 5.46E23 | 1.53E24 | 2.09E24 | 2.57E24 | 2.97E24 | 3.33E24 | 3.63E24 |
| 13 | 5.47E23 | 1.41E24 | 1.9E24 | 2.33E24 | 2.7E24 | 3.03E24 | 3.32E24 |
| 14 | 5.47E23 | 1.35E24 | 1.79E24 | 2.18E24 | 2.53E24 | 2.84E24 | 3.12E24 |
| 15 | 5.48E23 | 1.27E24 | 1.65E24 | 2E24 | 2.31E24 | 2.6E24 | 2.86E24 |
| 16 | 5.49E23 | 1.23E24 | 1.57E24 | 1.89E24 | 2.18E24 | 2.45E24 | 2.69E24 |
| 18 | 5.5E23 | 1.24E24 | 1.58E24 | 1.9E24 | 2.2E24 | 2.47E24 | 2.72E24 |
| 20 | 5.51E23 | 1.21E24 | 1.53E24 | 1.83E24 | 2.1E24 | 2.36E24 | 2.60E24 |
Table 3: Effective electron density (electron/g) of polymer composites for total photon interaction (with coherent).
| This work | Published Results | |||
|---|---|---|---|---|
| Sample code | ∑R/ρ (cm-1) | Sample | ∑R/ρ (cm-1)(22) | |
| Barite addition | (P1) | 8.58E-02 | Ordinary concrete | 3.41E-02 |
| (PB2) | 8.31E-02 | |||
| (PB3) | 8.04E-02 | |||
| (PB4) | 7.77E-02 | |||
| (PB5) | 7.50E-02 | |||
| (PB6) | 7.23E-02 | |||
| (PB7) | 6.96E-02 | |||
| Boron carbide addition | (PBC2) | 8.43E-02 | Magnetite concrete | 3.61E-02 |
| (PBC3) | 8.28E-02 | |||
| (PBC4) | 8.13E-02 | |||
| (PBC5) | 7.98E-02 | |||
| (PBC6) | 7.83E-02 | |||
| (PBC7) | 7.68E-02 | |||
| Barite and Boron carbide addition | (PBBC2) | 8.37E-02 | Barite-barite | 2.97E-02 |
| (PBBC3) | 8.16E-02 | |||
| (PBBC4) | 7.95E-02 | |||
| (PBBC5) | 7.74E-02 | |||
| (PBBC6) | 7.53E-02 | |||
| (PBBC7) | 7.32E-02 | |||
Table 4: Calculations of the fast neutrons effective removal cross-sections for glycidyl methacrylate with different ratio of barite and boron carbide composite.
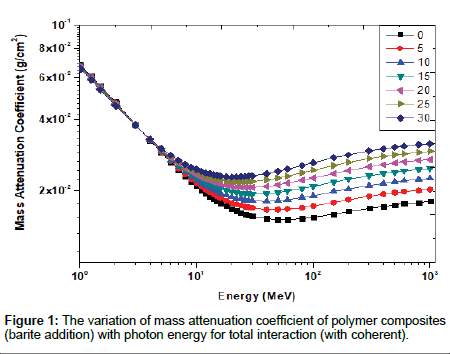
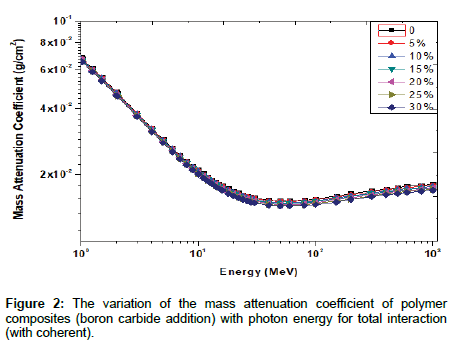
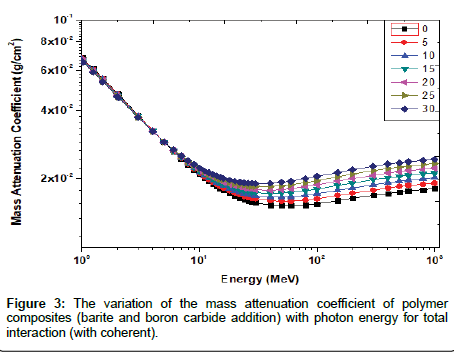
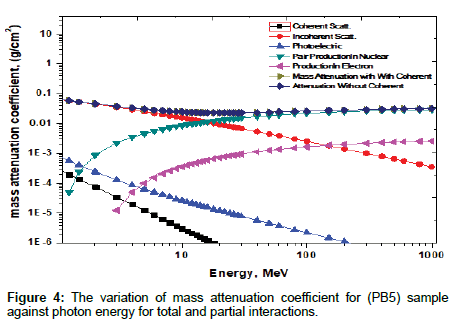
Mass attenuation coefficients
The dependence of mass attenuation coefficient μ/ρ of polymer composites to photon energy is shown in Figures 1-3. While in Figure 4 only results from (PB5) sample on the variations of the μ/ρ for total and partial photon interactions were shown. It is seen from the figure that different dominant interaction processes on different energy regions. There are three energy ranges relative to the partial processes: p h otoelectric absorption at low energies, incoherent (Compton) scattering at intermediate energies and pair production at high energies. In Figure 4, the curve of Compton scattering is split up because i t dependent on probability of photon interaction by incoherent scattering for each energy.
Figure 1: The variation of mass attenuation coefficient of polymer composites (barite addition) with photon energy for total interaction (with coherent).
Figure 2: The variation of the mass attenuation coefficient of polymer composites (boron carbide addition) with photon energy for total interaction (with coherent).
Figure 3: The variation of the mass attenuation coefficient of polymer composites (barite and boron carbide addition) with photon energy for total interaction (with coherent).
Figure 4: The variation of mass attenuation coefficient for (PB5) sample against photon energy for total and partial interactions.
Effective atomic number, Zeff
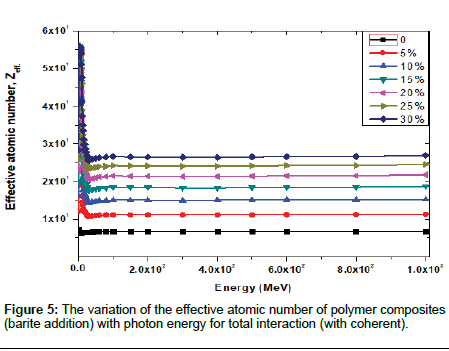
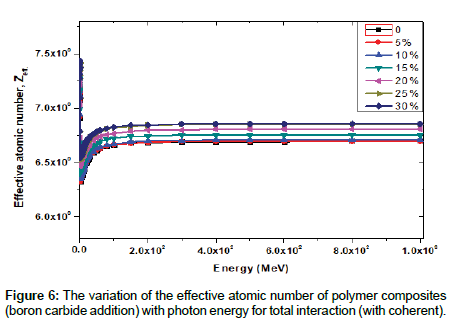
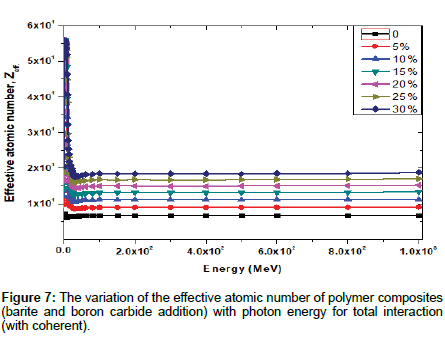
The value of Zeff for a composite material is a very useful parameter for some applications such as physical, technological and engineering. This value can provide an estimation of the chemical composition of the material and it can be also utilized in the computation of absorbed dose in radiation therapy etc. In this work, Zeff values for Polymer composites (equal proportions of barite and boron carbide) were calculated by using Eqn. (11) and given in Table 2.
The variation of Zeff of photon energy for total interaction processes in all-polymer composites is shown in Figures 5-7. These figures show that the minimum value of Zeff is found around intermediate energies (0.1>E<8 MeV). It is clear that Zeff increases with increasing of energy from 1 keV to 300 keV and then it remains constant even with further increase in energy.
Figure 5: The variation of the effective atomic number of polymer composites (barite addition) with photon energy for total interaction (with coherent).
Figure 6: The variation of the effective atomic number of polymer composites (boron carbide addition) with photon energy for total interaction (with coherent).
Figure 7: The variation of the effective atomic number of polymer composites (barite and boron carbide addition) with photon energy for total interaction (with coherent).
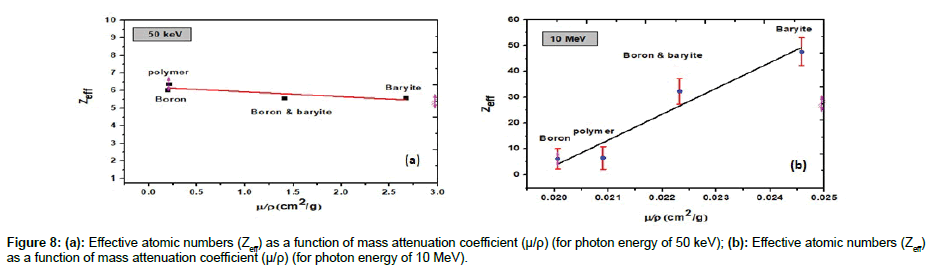
Figure 8a and 8b show plots of μ/ρ versus Zeff for the incident photon energy. As clearly seen that μ/ρ increases linearly with increasing Zeff. This work was carried out for low and intermediate photon energies. Photons in the keV range are important in radiation biology as well as in medical diagnostics and therapy. In the composite materials, the interaction (such as absorption and scattering) of γ-or X-rays is related to Zeff value of composite materials and the energy of incident photons. At low photon energies, the photoelectric interaction is the main photon interaction process and dependence of atomic number is dominant for the interaction of a photon with matter.
Figure 8: (a): Effective atomic numbers (Zeff) as a function of mass attenuation coefficient (μ/ρ) (for photon energy of 50 keV); (b): Effective atomic numbers (Zeff) as a function of mass attenuation coefficient (μ/ρ) (for photon energy of 10 MeV).
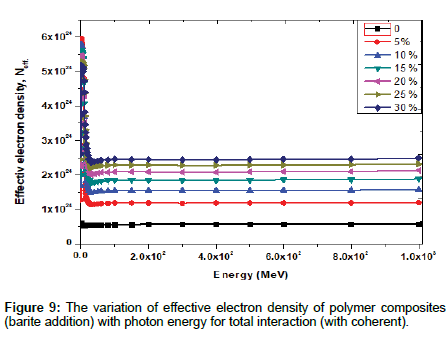
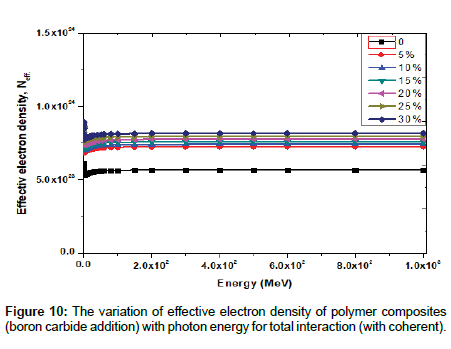
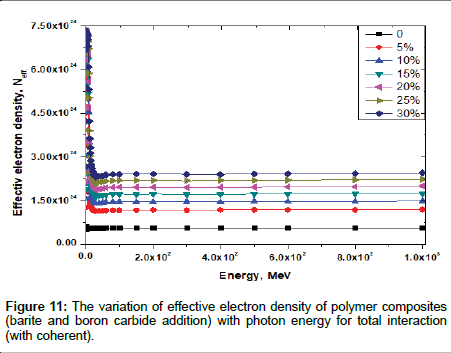
Effective electron density, Neff
The variation of Neff of polymer composites with photon energy for total photon interaction is shown in Figures 9-11. It is observed that Neff shows similar trends to Zeff.
Figure 9: The variation of effective electron density of polymer composites (barite addition) with photon energy for total interaction (with coherent).
Figure 10: The variation of effective electron density of polymer composites (boron carbide addition) with photon energy for total interaction (with coherent).
Figure 11: The variation of effective electron density of polymer composites (barite and boron carbide addition) with photon energy for total interaction (with coherent).
Figure 12: Effective removal cross-sections of fast neutrons for polymer composites.
Effective removal cross-sections of fast neutrons
The results of calculated (ΣR/ρ) for the investigated composites are given in Table 4. It can be seen from these tables that the obtained values for (ΣR/ρ) are ranged from 6.96E-02, for (PB7) sample, to 8.58E-02, for (P1) sample. The results obtained were compared with the special values of three types of concrete [22] as shown in Table 4, which showed a relative increase in the values of the investigated samples. This means that the investigated samples are more effective as fast neutron attenuators than the common materials used in that field.
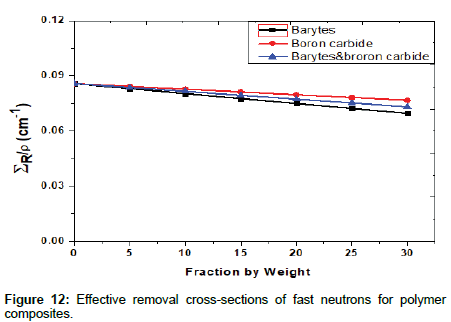
Figure 12 has shown the calculated effective removal crosssections of fast neutrons for polymer composites as a function of fraction by weight for each sample. It was found that the (ΣR/ρ) depends on the elemental composition and it is clear that the most important parameter affecting neutron attenuation is the amount of hydrogen in the sample. This can be attributed to the fact that the hydrogen has a higher value of (ΣR/ρ).
As shown from Figure 12, the higher concentration of hydrogen in the chemical composition of the polymer without any addition in comparison to that of the other samples with different ratios of barite and boron carbide explain the greater value of (ΣR/ρ) for the polymer in comparison to values of (ΣR/ρ) for other samples. While the low value of (ΣR/ρ) observed for (PB7) sample is mainly due to the low concentration of hydrogen in the material. Then, it is concluded that the concentration of hydrogen in the polymer is the most important parameter that affects the attenuation of fast neutrons in such materials.
At first sight, we can conclude from these results that the (P1) sample is the most effective material for neutron shielding, which is not true. For an effective attenuation of fast neutrons in the neutron shielding material, both moderator and absorber should exist in the sample. This is not the case for (P1) sample because it does not contain boron which is a good absorber to reduce the production of secondary gamma rays during the absorption of thermalized neutrons. So, the most effective materials for neutron shielding are (PBC7) sample which contains 30% boron carbide and has a high (ΣR/ρ).
As well as if we talk about a mixed beam of neutron and gamma rays, the effective shielding material is (PBBC7) sample. This due to, it’s containing a good absorber for both neutrons and gamma rays. So we can conclude that it is rather the sample (PBC7), (PBBC7) which is the most effective material for neutron and gamma-ray shielding because it has a relatively high (ΣR/ρ) and contains barites as a photon absorber.
Conclusion
The present study gives the values for the total macroscopic effective removal cross-section of fast neutrons (ΣR/ρ) and the gamma-rays mass attenuation coefficients, effective atomic numbers and effective electron densities of polymer composites reinforced with different percentages of barites and boron carbide (0-30%). The gamma-ray calculations were performed for the investigated samples over a wide range of photon energies from 1 keV to 1 GeV. The results obtained from this work show that the total macroscopic effective removal cross-section (ΣR/ρ) is dependent on chemical content and the total mass attenuation coefficient (μt) is dependent on the incident photon energy and chemical content.
The obtained values of the attenuation coefficient show that (PB) and (PBBC) composites have nearly the same attenuation curves and the attenuation coefficient of these two materials are slightly higher than (PBC) composite. I can also conclude from this work that (PBC7) composite is a good material for neutrons shielding applications, whilst (PB7) composite are slightly better than those of the other composite for gamma rays shielding applications. Finally, the (PBBC7) composite are slightly better than those of the other composite for mixed beam (neutrons and gamma-rays) shielding applications.
Moreover, the obtained results are helpful in understanding the interaction of neutron and γ-ray with polymer reinforced composites, which has been used in the fabrication of new shielding material. As well as, these results can be used as a database for designers of nuclear technology.
Acknowledgement
Author thanks Jouf University for their financial support through a research project No. 39/220.
References
- Jalali M, Mohammadi A (2008) Gamma ray attenuation coefficient measurement for neutron-absorbent materials. Radiat Phys Chem 77: 523-527
- Van den Heuvel F, Locquet JP, Nuyts S (2010) Beam energy consideration for gold nano-particle enhanced radiation tratement. Phys Med Biol 55: 4509-4520.
- El Haber F, Froyer G (2008) Transparent polymers embedding nanoparticles for X-rays attenuation. J Univ Chem Technol Metall 43: 283-290.
- Faccini M, Vaquero C, Amantia D (2012) Development of protective clothing against nanoparticle based on electrospun nanofibers. J Nanomater 1-9
- Hubbell HJ (1982) Photon mass attenuation and energy-absorption coefficients. Int J Appl Radiat Isot 33: 1269-1290
- Manohara SR, Hanagodimath SM (2007) Studies on effective atomic numbers and electron densities of essential amino acids in the energy range 1 keV-100 GeV. Nucl Instrum Methods B 258: 321-328
- Ozdemir Y, Kurudirek M (2009) A study of total mass attenuation coefficients, effective atomic numbers and electron densities for various organic and inorganic compounds at 59.54 keV. Ann Nucl Energy 36: 1769-1773
- Içellia O, Yalç�?±n Z, Okutan M, Boncukçuo�?�?lu R, �?�?en A (2011) The determination of the total mass attenuation coefficients and the effective atomic numbers for concentrated colemanite and Emet colemanite clay. Ann Nucl Energy 38: 2079-2085.
- Hine GJ (1952) The effective atomic numbers of materials for various gamma ray interactions. Phys Rev 85: 725.
- Akkurt I (2009) Effective atomic and electron numbers of some steels at different energies. Ann Nucl Energy 36: 1702-1705
- Berger MJ, Hubbell JH (1987) XCOM: Photon cross-section on a personal computer. U.S. Department of Commerce, National Bureau of Standards, Office of Standard Reference Data.
- Blizard EP, Abbott LS (1962) Reactor handbook. Volume III, part B, Shielding (2nd edn). Interscience Publishers, New York.
- Duderstadt JJ, Hamilton LJ (1976) Nuclear reactor analysis. John Wiley and Sons, New York, USA
- Kaplan MF (1989) Concrete radiation shielding. John Wiley and Sons, New York, USA
- Glasstone S, Sesonske A (1986) Nuclear reactor engineering (3rd edn). CBS Publishers and Distributors, India
- Profio AE (1979) Radiation shielding and dosimetry. John Wiley and Sons, New York, USA.
- Wood J (1982) Computational methods in reactor shielding. Pergamon Press Inc.
- Martin JE (2000) Physics for Radiation Protection (3rd edn). John Wiley and Sons, New York, Toronto.
- Shultis JK, Faw RE (2008) Fundamentals of nuclear science and engineering (2nd edn). CRC Press, Boca Raton, FL.
- Chilton AB, Shultis JK, Faw RE (1984) Principles of radiation shielding. Prentice-Hall, Englewood Cliffs, NJ.
- El-Khayatt AM (2010) Calculation of fast neutron removal cross-sections for some compounds and materials. Ann Nucl Energy 37: 218-222.
- El-Khayatt AM, El-Sayed Abdo A (2009 ) MERCSF-N: A program for the calculation of fast neutron removal cross sections in composite shields. Ann Nucl Energy 36: 832-836.
