Review Article, Res Rep Math Vol: 2 Issue: 4

The Role of Finsler Geometry and its Extensions on the Structure of Gravitation and Cosmology

Stavrinos PC^1* and Triantafyllopoulos A²

Department of Forestry and Biodiversity, Tripura University, Suryamaninagar, Agartala, India

Department of Physics, National and Kapodistrian University of Athens, Athens, Greece

*Corresponding Author : Stavrinos PC
Department of Mathematics, National and Kapodistrian University of Athens, Panepistimiopolis 15784, Athens, Greece
E-mail: pstavrin@math.uoa.gr

Received: September 01, 2018 Accepted: December 12, 2018 Published: December 19, 2018

Citation: Stavrinos PC, Triantafyllopoulos A (2018) The Role of Finsler Geometry and its Extensions on the Structure of Gravitation and Cosmology. Res Rep Math 2:4.

Abstract

Keywords: Finsler geometry; Gravitation; Cosmology

Introduction

The geometry which has constituted the base for descriptions of space-time that manifest curvature is Riemann geometry. Its application in the structure and description of gravity is connected with local isotropy of space-time. The metric properties of this geometry verify the observational descriptions developed in general theory of relativity, e.g. geodesics and deviations of geodesics.

In the framework of physical geometry i.e. the geometry which studies the principles of analysis of space in relation to the objects moving in it and interacting, the geometrical properties of space-time are studied. In the study of such a theory, gravity can be represented in terms of geometrical objects such as the curvature, which constitutes an important tool for studying the nature of the universe. In this approach, a point may be replaced by an event.

An interesting generalization of the Riemannian metric is presented when one additionally considers the direction or velocity of a point-particle in geometrical objects. In this case we get a metrical extension of Riemann geometry which is called Finsler geometry, also known as geometry of variational calculus. Such a geometry can be used when space-time is locally anisotropic. In this form of space-time Riemann geometry is incapable of describing many physical events in spacetime.

The last decade a growth of interest from the scientific community in applications of Finsler and Finsler-like and Lagrange-Finsler geometries has significantly contributed in the development of this topic mainly in gravitation, general relativity and cosmology. We mention some of the works that played a role in this direction [1-26].

The study of Finsler geometry can be traced back to a famous lecture by Bernhardt Riemann in 1868: “On the hypotheses which lie at the bases of geometry” [27]. In this lecture, Riemann discusses the ways in which an n-dimensional manifold can be equipped with a metric structure. His attention was focused on the case in which the line-element (distance between two neighboring points) may be expressed by the square root of a quadratic differential expression, which later lead to the development of Riemann geometry. He also mentioned a case where the line-element can be expressed as the fourth root of a quartic expression, however he reasoned that the investigation of this form would take considerable time and throw little new light on the theory of space, so he restricted himself to the simplest form.

Both forms proposed by Riemann were positively homogeneous of first degree in the differentials and convex in them. A natural generalization of these forms would be the definition of line-element as

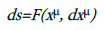
with the aforementioned properties. The first study of a space equipped with this form was made in the thesis of Paul Finsler, supervised by the Greek mathematician Constantin Carathéodory and inspired by the work of the latter on the geometrization of the calculus of variation, hence the name “geometry of the variational calculus”. In the following years many important mathematicians such as Elie Cartan, L. Berwald, Makoto Matsumoto, Akitsugu Kawagutsi, Veblen, Bliss, Landsberg, John Lighten Synge, James Henry Taylor, Hanno Rund studied the geometry extensively, generalized several results from Riemann geometry and created a richer framework with various types of connections, curvatures etc [28]. A very important result of the study of these spaces is that a function F(x,y), y ^μ=dx ^μ/dλ with the above-mentioned properties can be reduced to the form

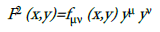
where

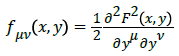
So, the notion of a locally anisotropic metric is introduced.

Considering the above, we can express the line element in a Euclidean, Minkowski, Riemann or Finsler space as:

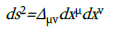
Where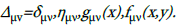

The symbol δ_μν is the Kronecker delta, η_μν=diag(-1,1,1,1) is the Minkowski flat space-time metric tensor, g_μν(x) is the Riemann metric tensor and f_μν(x,y) is the Finsler metric tensor. In the above expression, the metric tensor Δ_μv is acting like a “machine” that determines the distance in a space and the norm of tangent vectors on it. In physical applications, the metric tensors g_μν(x) and f_μν(x,y) of Riemann and Finsler geometry respectively play the role of gravitational potentials. We remark that in the tangent space over a fixed point x₀ on a Finsler manifold the norm of the tangent vector y is expressed as

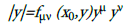
From this relation it becomes apparent that a tangent space on a Finsler manifold is actually a Riemann space.

The consideration of Finsler geometry in the base n-dimensional manifold is a first step for experimental study of an anisotropic structure of spacetime. For a well-defined Finslerian geometric structure it is required that this geometry is considered in the framework of a 2n-dimensional tangent bundle, a structure which consists of the union of the tangent spaces at all the points of a base n- dimensional differential manifold. The 2n-dimensional tangent space of a tangent bundle is split in a non-unique way into an n-dimensional “horizontal” and an n -dimensional “vertical” part 17, the first is usually interpreted as an extension of the base manifold’s tangent space while the latter is a result of the additional degrees of freedom of this framework. The splitting is completely defined by the introduction of Ehresmann’s nonlinear connection, a geometrical structure that connects the space of the “external” x and the “internal” y variables. Significant studies of the nonlinear connection were made by Synge, Taylor and A. Kawaguchi [29,30].

Nonlinear connection plays a fundamental role in the theory of tangent Lorentz bundles, as the splitting of their 8-dimensional tangent space is something desirable from a physical point of view [31]. The horizontal 4-dimensional subspace is used to describe the Finslerian extensions of the usual spacetime tensors, while the vertical 4- dimensional subspace can give rise to new physical quantities. The geometrical concepts of a Finsler manifold such as the metric structure, connections, curvatures etc. are extended to the additional degrees of freedom offered by the vertical space, see [17,32] for a full treatise. These extensions can offer new perspectives in physical applications, as we will see later. The geometrical structures that preserve the splitting induced by the nonlinear connection (i.e. only have pure horizontal or vertical terms) are called distinguished. The total tangent space of the tangent bundle is associated with a Whitney sum of the horizontal and vertical space.

In physical applications, Finsler and Finsler-like geometries can be used. By the term Finsler-like we refer to a geometry with a locally anisotropic metric tensor that does not come from a generating function F(x,y) with the aforementioned properties. To construct a Finsler or Finsler-like geometry for a locally anisotropic gravity theory we need a triplet of fundamental geometric objects: The total metric structure G , the non-linear connection N and a distinguished linear d-connection D adapted to N . A d-connection preserves by parallelism the horizontal and vertical structure of space.

In applications of Finsler and Finsler-like geometries to gravitation and cosmology or spinor structures, a compatible (metric, canonical) linear connection is necessary in order to ensure the norm conservation of a vector or a wave vector. It was E. Cartan who first developed a metric linear connection in the framework of a Finsler manifold [33]. His method treated x and y as independent variables of the geometry, although his formalism remained on the base manifold. His connection for x displacements essentially constitutes a direct generalization of the Riemannian Christoffel connection with the partial derivatives replaced by a non-commutative δ -derivative operator. The connection for the y displacements is encoded by the Cartan torsion tensor, a structure which gives a measure for the deviation from Riemann geometry.

Later, a more general linear canonical d-connection was developed on the tangent bundle geometry [31]. The frame of the horizontal space associated with a nonlinear connection is non-commutative (non-holonomic) in general, in contrast to the commutative coordinate frame of a manifold, and this inevitably gives rise to torsion terms. With this connection, general relativity is extended in a metrically compatible way in the framework of the tangent bundle (although with nonzero torsion). For a metrical structure which has the same horizontal (g_μν (x,y)) and vertical (v_μν (x,y)=g_μν (x,y)) coefficients and a Cartan-type nonlinear connection, the canonical d-connection reduces to Cartan’s connection on the tangent bundle.

Another fundamental form of connection in Finsler geometry is the Berwald connection. This was the first linear connection that was introduced in a Finsler space and is characterized by simplicity of formalism and torsion freeness. To achieve this, Berwald connection sacrifices metric compatibility [34]. Another non-metrical connection similar but somewhat simpler than Berwald’s is the Chern connection [35]. The non-compatibility of these connections in all the tangent bundle constitutes a weak point regarding their applications to gravitation and cosmology.

Applications in Various Topics of Science

Finsler geometry has been applied in many branches of science aside from gravitation [36]. It has been applied in mathematical biology (Peter Antonelli) with studies in ecology, social interactions, predator-prey dynamics and evolution theory. In information thermodynamics (Roman Ingarden, R. Mrugala) the concept of relative information (entropy) is used to define a Riemannian structure on the spaces of thermodynamic parameters. For nonequilibrium systems the structure becomes Finslerian [37]. There have also been applications of Finsler geometry in (crystal, physiological, electron) optics. In the topic of seismology, the seismic wavefront in anisotropic media has been described using Finsler geometry [19]. The shape of the wavefront is not a circle in this case but a convex curve called superellipse.

Applications in Gravitation

Deviations of geodesics have been studied in the framework of the tangent bundle in [38,39]. A fundamental work in the subject of Raychaudhuri equations for congruences on the Finsler tangent bundle particularly for F-R spacetimes has been studied in [13,16,23], A different approach is given in [3,10]

There has been some progress regarding the formulation of classical physical fields in Finsler spacetimes. Various efforts to produce field equations for the generalized metric tensor can be found in the literature. A tangent Lorentz bundle is itself a differentiable 8- dimensional manifold which can be equipped with a generalized metrical compatible connection and a corresponding curvature tensor, so it has been a common practice over the years to consider an 8- dimensional version of Einstein field Equations on it using these quantities in the place of the classic ones [17,32]. The osculating Riemannian space approach can give another solution to this matter. With this method one can reduce the Finslerian spacetime to a “Riemannian” one [28,40]. The known structures and equations from general relativity can be used on this space, however the geometrical structures will generally come with extra terms due to their Finslerian origin, see for example [22]. An approach using generalized Bianchi identities on a Berwald space with Chern connection to produce field equations is presented in [25]. The first time a variational principle was used to produce field equations from an action on a Finsler space was in 2007 [5]. An application of this principle on the tangent bundle using a Chern connection and curvature to calculate the horizontal metric can be found in [20]. An alternative method can be found in where the variational principle is applied on the unit tangent bundle with F(x,y) playing the role of the dynamic variable [12]. In the variational principle for a Hilbert-like action is applied on the tangent bundle equipped with a canonical d-connection and field equations for the horizontal and vertical parts of the metric tensor are obtained [18].

There have also been some efforts to incorporate the electromagnetic field in the framework of the tangent bundle. It is proved that for a Cartan connection the electromagnetic field tensor produced by an isotropic vector potential obeys the same Bianchi identities as in general relativity [41]. A treatment for a locally anisotropic vector potential is presented by Voicu [21]. An approach using the differential form of Maxwell equations for an isotropic vector potential can be found [18].

Geometrical flows for spaces characterized by nonlocality of higher degree can be found in study by Alexiou and Stavrinos [1,14].

Non-commutative and non-holonomic structures on the (Lorentzian) tangent bundles and applications in general relativity and cosmology have been established in a series of papers by S. Vacaru and his collaborators [16,17,24].

The Finsler-Randers Cosmological Model

In the present section we discuss the physical and cosmological advances in the field of Finsler and Finsler-like geometries. Particular attention over the last decade has been paid to the so-called Finsler-Randers (F-R) cosmological model [22]. The main idea is to use a Randers point-particle Lagrangian as a generating function:

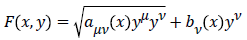
The first term on the right-hand side is just the general relativistic point-particle Lagrangian for the Riemannian metric a_μν(x) and the second encodes the deviation from isotropy via the one form field b_ν(x). We can say that the resulting Finsler-Randers metric space connects the Riemannian structure with the Finslerian one.

In a study by Basilakos [2] it is shown that F-R cosmology shares the same Hubble expansion with the DGP braneworld model, although the geometrical background of the two theories is different. The matter perturbation dynamics for these models is found to be slightly different.

A complete analysis of matter perturbation dynamics for the model is made in a study by Papagiannopoulos [11]. The asymptotic perturbation growth index for cold dark matter is calculated to be lower than the one from cosmology.

The postulate of local anisotropy and its relation with Finsler-like geometries

Finsler geometry incorporates the postulate that spacetime is locally anisotropic, in the sense that physical quantities depend on the direction of the observer. This automatically requires that every part of matter inside spacetime must be associated with a motion. In general relativity this is postulated ad hoc (everything has nonzero 4-velocity) but in Finsler theory it is a prerequisite of the geometry itself. That means Finsler geometry ensures that matter dynamics take place.

In a study by Cohen [4] Einstein’s principle of Special Relativity is generalized so that spacetime symmetries are certain subgroups of the Poincaré group, resulting in the so-called Very Special Relativity (VSR). A characteristic of VSR is that it respects CPT symmetry. It was proved in a study by Gibbons [6] that only a certain subgroup of the Poincaré group is physically acceptable, and that the construction of a point-particle Lagrangian that is invariant under this subgroup is of Finsler form. Incidentally, this form was first proposed by Yu. Bogoslovsky in 1977 [42].

In a study by Kouretsis [9] the Bogoslovsky metric form is generalized to incorporate curved spacetime. It is argued that anisotropy in Finsler spaces may come from local Lorentz violation. An extension of pp-wave spacetime solution for a Finsler-Berwald space using a generalized Bogoslovsky line-element is given in a study by Fuster [26].

The subject of Lorentz symmetry breaking in particle physics has been central in the work of A. Kostelecký and collaborators. In 1989 A. Kostelecký and S. Samuel proved that an unstable perturbative string vacuum can naturally cause a spontaneous Lorentz symmetry breakdown [43]. Other cases of spontaneous Lorentz symmetry breaking were later discovered in grand unified theory candidates. It was found that a spontaneous CPT breaking in string theory can leave a signature in certain particle systems, and an appropriate extension of the minimal standard model of particle physics was proposed (Standard Model Extension – SME) [44]. The familiar standard model can be viewed as a low-energy limit of a theory that is Lorentz covariant for the observer but not for the particle dynamics [45]. Various experiments for the detection of Lorentz and CPT spontaneous breaking have been proposed and experimental bounds have been set on the theory, see Kostelecky [7] and references therein. Classical Lorentz violating point-particle Lagrangians have been constructed from SME counterparts [8].

Lorentz and CPT violations can be associated with local anisotropy of spacetime. It is expected that Finsler-like theories and SME will be compatible as they both share the same geometrical principles.

The Dark Energy Problem

In the last 30 years, observations have shown that the universe is expanding at an accelerated rate and standard FRW cosmology with ordinary matter fields (cold dark matter, radiation) is unable to explain this. It has been considered that the introduction of a cosmological constant Λ in the classical Hilbert action of general relativity (GR) can explain this accelerated expansion, however its value cannot be calculated from the theory and must be set by hand to agree with observations. There have been efforts to associate the cosmological constant with the vacuum energy of quantum fields but the calculated value deviates from the one suggested by observations. The cause of the accelerated expansion is called “dark energy”, though we really know very little about it.

Several modified gravity theories have been proposed as candidates to explain theoretically the observations, usually by modifying the Hilbert action in a Riemannian framework. Finsler and Finsler-like theories have a different approach, as they modify the geometry itself rather than the action. In general, metrical extensions of Riemann geometry can be provided with a Finslerian geometrical structure in a manifold which leads to generalized gravitational field theories. During these years there has been a rapid development of applications of Finsler geometry particularly of the F-R model mainly in the topics of general relativity, astrophysics and cosmology. It has been found by Stavrinos et al. [22] that the F-R field equations provide a Hubble parameter that contains an extra geometrical term which can be used as a possible candidate for dark energy.

In a study by Kouretsis [9] the Bogoslovsky Finslerian metric function is generalized for curved spacetime specifically for a spatially flat cosmology. The resulting generalization of FRW cosmology can account for cosmological acceleration.

On the other hand, it has been shown that the equations of cosmological evolution for a flat FRW cosmology extended on the tangent bundle provide extra terms compared to classical cosmology of GR that can incorporate an accelerated expansion [18]. Those terms come directly from the geometry and can be associated with the extra degrees of freedom provided by the internal variables y. Specifically, the vertical part of the metric may act as a potential in y-space from which the scalar function S(x,y) that provides accelerating expansion is derived. The equations of cosmological evolution actually take the same form with the classical Friedmann Equations of GR if one sets S=-2Λ=const. Although S acts as an effective cosmological constant, it is generally an anisotropically polarized dynamical variable and can be used to elaborate on much more general cosmological dynamics where anisotropy is inherently considered [15,16]. One may say that a portion of the universe’s anisotropy is transformed to dark energy as the universe becomes more isotropic.

It is interesting to remark here that an analogous statement has been made for general relativistic cosmology with a Bianchi type-I metric. Particularly, in the very early universe the particle-antiparticle creation process can account for the creation of real massless particles in the condition that the expansion is non-adiabatic and anisotropic at this time [46]. Thus, the energy of anisotropy is dissipated and transformed into radiation as the universe cools down and becomes isotropic.

On a similar note, it is argued that for certain toy models, the generalized energy-momentum tensor can be approximated by a cosmological constant with possible locally anisotropic polarizations depending on (x, y) [15].

Conclusion

In the next years, it is expected that there will be a development of applications of Finsler and Finsler-like geometries, mainly in the topics of general relativity, gravitation and cosmology which can contribute in solving problems for a universe with a weak anisotropic field in the corresponding sectors.

References

1. Alexiou M, Gheorghiu T, Stavrinos PC, Vacaru O, Vacaru SI (2015) Nonholonomic ricci flows and Finsler–Lagrange f (R, F, L)–modified gravity and dark matter effects. In: Proceedings, 14th Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Astrophysics, and Relativistic Field Theories (MG14), Rome, Italy.
2. Basilakos S, Stavrinos P (2013) Cosmological equivalence between the Finsler-Randers spacetime and the DGP gravity model. Phys Rev D 87: 043506.
3. Caponio E, Javaloyes MA, Sánchez M (2011) On the interplay between Lorentzian Causality and Finsler metrics of Randers type. Rev Mat Iberoamericana 27: 919-952.
4. Cohen AG, Glashow SL (2006) Very special relativity. Phys Rev Lett 97: 021601.
5. Garas'ko GI (2007) On Field Theory and some Finsler Spaces arXiv:math-ph/0702037v2.
6. Gibbons GW, Gomis J, Pope CN (2007) General very special relativity is Finsler geometry. Phys Rev D 76: 081701.
7. Kostelecky VA, Russel N (2011) Data tables for Lorentz and CPT violation. Rev Mod Phys 83: 11.
8. Kostelecky VA, Russell N (2010) Classical kinematics for Lorentz violation. Phys Lett B 693: 443-447.
9. Kouretsis AP, Stathakopoulos M, Stavrinos PC (2009) General very special relativity in Finsler cosmology. Phys. Rev D 79: 104011.
10. Minguzzi E (2015) Raychaudhuri equation and singularity theorems in Finsler spacetimes. Class Quantum Grav 32: 185008.
11. Papagiannopoulos G, Basilakos S, Paliathanasis A, Savvidou S, Stavrinos PC (2017) Finsler–Randers cosmology: dynamical analysis and growth of matter perturbations. Class Quantum Grav 34: 225008.
12. Pfeifer C, Wohlfarth MN (2012) Finsler geometric extension of Einstein gravity. Phys Rev D 85: 064009.
13. Stavrinos PC (2012) Weak gravitational field in Finsler-Randers space and Raychaudhuri equation. Gen Rel Gravit 44: 3029-3045.
14. Stavrinos PC, Ikeda S, Alexiou M (2018) On the metric structure and connection considerations of gravitational field in fInsler spaces. J Phys Res Appl 2:  1.
15. Stavrinos PC, Vacaru SI (2013) Cyclic and Ekpyrotic Universes in Modified Finsler Osculating Gravity on Tangent Lorentz Bundles. Class Quant Grav 30: 055012.
16. Stavrinos PC, Vacaru O, Vacaru SI (2014) Modified Einstein and Finsler like theories on tangent Lorrentz bundles. Int J Mod Phys D 23: 1450094.
17. Vacaru S, Stavrinos P, Gaburov E, Gonta D (2005) Clifford and Riemann–Finsler Structures in Geometric Mechanics and Gravity, Geometry Balkan Press, Bucharest, Romania.
18. Triantafyllopoulos A, Stavrinos PC (2018) Weak field equations and generalized FRW cosmology on the tangent Lorentz bundle. Class Quantum Grav 35: 085011.
19. Yajima T, Nagahama H (2009) Finsler geometry of seismic ray path in anisotropic media. Proc R Soc A 465: 1763-1777.
20. Voicu N (2010) New Considerations on Einstein Equations in Pseudoâ�?Finsler Spaces. AIP Conference Proceedings 1283: 249.
21. Voicu N (2011) On the fundamental equations of electromagnetism in Finslerian Spacetimes. PIER 113:  83-102.
22. Stavrinos PC, Kouretsis AP, Stathakopoulos M (2007) Friedman-like Robertson–Walker model in generalized metric space-time with weak anisotropy. Gen Rel Gravit 40: 1403-1425.
23. Stavrinos PC, Alexiou M (2018) Raychaudhuri equation in the Finsler-Randers spacetime and Generalized scalar-tensor theories. Int J Geom Methods Mod Phys 15: 3.
24. Vacaru SI (2018) On axiomatic formulation of gravity and matter field theories with MDRs and Finsler-Lagrange-Hamilton geometry on (co)tangent Lorentz bundles, arXiv:1801.06444v.
25. Li X, Chang Z (2010) Chinese Physics C. 34: 1.
26. Fuster A, Pabst C (2016) Finsler pp-waves. Phys Rev D 94: 104072.
27. Riemann B (1873) On the Hypotheses Which lie at the Bases of Geometry. Nature 8: 14-17.
28. Rund H (1959) The Differential Geometry of Finsler Spaces, Springer, Berlin, Germany.
29. Kawaguchi A (1952) On the theory of Nonlinear connections I. Tensor NS 2: 123-142.
30. Kawaguchi A (1956) On the theory of Nonlinear connections II. Theory of Minkowski spaces and of nonlinear connections in a Finsler space.Tensor NS 6: 165-199.
31. Miron R, Watanabe S, Ikeda K (1987) Some connections on tangent bundle and their applications to general relativity. Tensor NS 46: 1987.
32. Miron R, Anastasiei M (2012) The geometry of Lagrange spaces: theory and applications. Springer Science & Business Media.
33. Cartan E (1934) Les espaces de Finsler, Hermann, Paris, London.
34. Matsumoto M (1986) Foundations of Finsler Geometry and Special Finsler Spaces, Kaiseisha Press.
35. Bao D, Chern SS, Shen Z (2000) An introduction to Riemann-Finsler geometry, Springer-Verlag, New York, USA.
36. Antonelli PL, Ingarden RS, Matsumoto M (1993) The Theory of Sprays and Finsler Spaces with Applications in Physics and Biology, Springer Science, USA.
37. Mrugala R (1992) Riemannian and Finslerian geometry in thermodynamics. Open Systems & Information Dynamics 1: 379-396.
38. Asanov GS, Stavrinos PC (1991) Finslerian deviations of Geodesics over tangent bundle. Rep Math Phy 30: 63-69.
39. Stavrinos PC, Kawaguchi H (1993) Deviation of geodesics in the gravitational space of Finslerian space-time. Memorial of Shonan Institute of Technology 27: 35-40.
40. Asanov GS (2012) Finsler geometry, relativity and gauge theories. Springer Science & Business Media, USA.
41. Stavrinos PC, Diakogiannis FI (2004) Finslerian structure of anisotropic gravitational field. Gravitation & Cosmology 10: 269-278.
42. Bogoslovsky GY (1977) A special relativistic theory of the locally anisotropic space-time. Il Nuovo Cimento B 40: 116-134.
43. Kostelecky VA, Samuel S (1989) Spontaneous breaking of Lorentz symmetry in String Theory. Phys Rev D 39: 683.
44. Colladay D, Kostelecky VA (1997) CPT violation and the standard model. Phys Rev D 55: 6760.
45. Colladay D, Kostelecky VA (1998) Lorentz-violating extension of the standard model. Phys Rev D 58: 116002.
46. Starobinskii AA (1981) Evolution of small perturbations of isotropic cosmological models with one-loop quantum gravitational corrections. JETP Letters 34: 438-441.