Research Article, Geoinfor Geostat An Overview Vol: 6 Issue: 1
A Hybrid Model Using Time Series and Markov Chain for the Detection of the Main Periodicities on the Temperature Data in Nisyros Volcano, South Aegean
Marsellos AE1*, Tsakiri KG2, Kapetanakis S3 and Kyriakopoulos K4
1Department of Geology, Environment, and Sustainability, Hofstra University, Hempstead, USA
2Department of Information Systems and Supplied Chain Management, Rider University, Lawrenceville, USA
3School of Computing, Engineering, and Mathematics, University of Brighton, Brighton, UK
4Departmet of Geology and Geoenvironment, National and Kapodistrian University of Athens, Greece
*Corresponding Author : Marsellos AE
Department of Geology, Environment, and Sustainability, Hofstra University, Hempstead, NY 12192, USA
Tel: +1-516-463-5567
Fax: 516-463-5120
E-mail: antonios.marsellos@hofstra.edu
Received: November 17, 2017 Accepted: January 22, 2018 Published: January 29, 2018
Citation: Marsellos AE, Tsakiri KG, Kapetanakis S, Kyriakopoulos K (2018) A Hybrid Model Using Time Series and Markov Chain for the Detection of the Main Periodicities on the Temperature Data in Nisyros Volcano, South Aegean. Geoinfor Geostat: An Overview 6:1. doi: 10.4172/2327-4581.1000177
Abstract
Nisyros volcano has shown a series of volcanic and seismo-tectonic events including recent volcanic phreatic eruptions intruding an impermeable layer near the surface. Geological and atmospheric phenomena contribute to the heat output from the hydrothermal system. To monitor the temperature fluctuations from a vent gas emission in Nisyros, a temperature sensor has been installed in a fumarole near the Lofos and Laki sites. Raw and decomposed temperature data were analyzed to determine the cycles of heat contribution at the surface from the endogenic volcanic activity and from the interaction with the atmospheric temperature. The time series decomposition using Kolmogorov-Zurbenko filter and the Markov chain approach have been utilized as complementary tools for the determination of the main periodicities on the temperature data. The Kolmogorov-Zurbenko filter is used for the time series decomposition of the temperature data into the longand
short term component of the time series. Markov chain analysis was used to determine probabilistically the periodicity in the temperature data and aggregate load impact in forecasting. Using spectral analysis and cluster analysis we determine the main periodicities of the longand short term cycles of heat contribution. Raw temperature data have shown an accelerated frequency of hourly temperature decreases at the surface. Small temperature decreases occur within the warmer atmospheric temperatures and dramatic temperature decreases occur during colder atmospheric temperatures. A physical or a mechanical phenomenon may prevent heat from reaching the surface. The time series decomposition performs well in long term cycles while the Markov chain performs better in short term cycles.
Both periods are related to cyclones that occur in the Aegean Sea. Since Nisyros is an island, the temperature measurements are probably affected by various phenomena (cyclones, sea tides) that occur in the sea and affect the hydrothermal convection.
Keywords: Decomposition of time series; Kolmogorov-Zurbenko filter; Markov chain analysis; fumarole’s time series temperature data; Spectral analysis; Hydrothermal activity; Volcanic monitoring
Introduction
A temperature logger of a volcanic surface such as in a fumarole may not directly reflect the various volcanic endogenic activities which are masked by interferences from other heat sources or phenomena. Volcanic monitoring is a rapid evolving field which requires sometimes a sophisticated data post-processing for removing interferences that mask endogenic volcanic activity. In active volcanoes such as in Greece, where nearly all the volcanic centers along the active Hellenic volcanic arc have erupted within the past three million years, and few volcanoes like Nisyros and Santorini have shown very recent eruptions, volcanic monitoring using advanced computational filtering techniques is necessary. Nisyros’ latest eruption of mud and altered rocks took place in 1873 [1]. Since then fumaroles continue to output heat originating from the active hydrothermal system beneath and, perhaps, rooted to a magma chamber they indicate the ongoing potential for further eruptions. Monitoring of the fumarole’s surface temperature, both the raw and the decomposed data, may allow monitoring of the endogenic volcanic activity.
In Nisyros, sealing of the upper bound of the hydrothermal system near the surface, above the condensate zone may take place by impermeabilization of the cover due to self-sealing [2]. This is a similar phenomenon to the one previously proposed [3], and it forces an accumulation of heat underneath the impermeable layer while the fumarole’s conduits receive less heat and show a temperature fall. Pressure distribution from the temperature fluctuation brings aquifers and fracture system close to becoming mechanically unstable with respect to their confining burden [4]. An imbalance between the internal fluid pressure and external atmospheric pressure can then trigger hydrothermal instability and further eruptions [5]. We think that a similar phenomenon may take place in Nisyros volcano and decomposing of time series data may provide insight at the endogenic volcanic activity.
Study Area
Nisyros island is an active composite volcano that belongs to the Hellenic Arc. It was built during the last 100 kyrs [6]. Multiple explosions formed a 3.8 km caldera less than 24,000 y.B.P. Rising magma derives as a consequence of the dehydration of the northward subducting African plate beneath the overriding South Aegean microplate. At the northern part of the caldera a series of daciticrhyodacitic domes rose above the caldera floor, while the south part, at Laki and Lofos, where the temperature logger was installed, has been affected by recent hydrothermal activity, argillic alteration caused by fumarolic fluid reaction, and a NE-trending fracture system.
Two wells have been previously installed [7], and the second well, Nisyros-2, is the closest to the logger site and encountered mostly talus and alluvial debris filling the caldera depression followed by deeper tephra and lavas. The well has shown two sections of permeable layers, a shallow layer from 250 to 350 m depth and a deeper one from 1000 m to 1350 m. The first layer shows multiple minerals associated with phyllitic-zeolitic hydrothermal paragenesis and temperatures reaching from 120° to 180°C. The presence of chlorite denotes that seawater has contributed to the condensate zone. The deeper permeable zone occurs from 1000 to 1350 m with temperatures reaching up to at least 290°C. The temperatures that have been measured in this well reflect a propylitic hydrothermal mineralization. This zone also shows chlorite as evidence of seawater input into the hydrothermal system.
Pre-volcanic basement is not exposed on Nisyros island in contrast to the other volcanic centers of the Hellenic arc. At the center of the caldera a carbonate sequence is not present, though one has been found at the second well, farther from the center. Mostly fragments, alluvium sediments, debris and talus compose the center of Nisyros caldera where argillic alteration has caused impermeabilization above the shallow permeable layer from 250 to 350 m.
Hydrothermal circulation in Nisyros island has been previously described [2] and follows a similar model with that of Yellowstone or Waiotapu with characteristics of hydrothermal [8] eruptions driven by expansion of hydrothermal fluids against atmospheric pressure. Nisyros caldera continues to form through seismo-tectonic operation of NE-trending faults, causing volcanic and recent phreatic eruptions followed by hydrothermal release of heat towards the surface. The latest eruption of mud and altered rocks in 1877 [1] with a powerful emission of a steam has probably encouraged argillic alteration and formation of an impermeable layer near the center of caldera. Those eruptions were recently described as phreatic eruptions involving the interaction of meteoric, seawater, and heat forming craters [2]. Those eruptions in Nisyros were thought to be initiated by fracturing due to earthquakes [9]. Fumaroles allow the release of the accumulated heat closer to the caldera’s surface, and monitoring of the associated temperature data may allow observation of the upper hydrothermal zone activity or endogenic volcanic behavior.
Materials and Methods
For this study we use the raw and decomposed temperature data from a logger installed at the surface of a fumarole in Nisyros volcano. Raw data shows a variable frequency of temperature drops that may be related to geological phenomena while the decomposed data show constant frequencies and periodicities reflecting mostly atmospheric phenomena. To decompose the raw temperature data we use a combination of two different approaches to determine and explain the main periodicities of the fumarole’s surface temperature time series. The Kolmogorov-Zurbenko (KZ) filter is combined with the Markov chain process. Both methods are introduced in the following sections and were applied to time series decomposed data for the detection of the main periodicities in the temperature data. Those periods have been determined based on spectral analysis and cluster analysis and they provide a physical explanation for the main periods of the temperature data in the volcano island.
Data
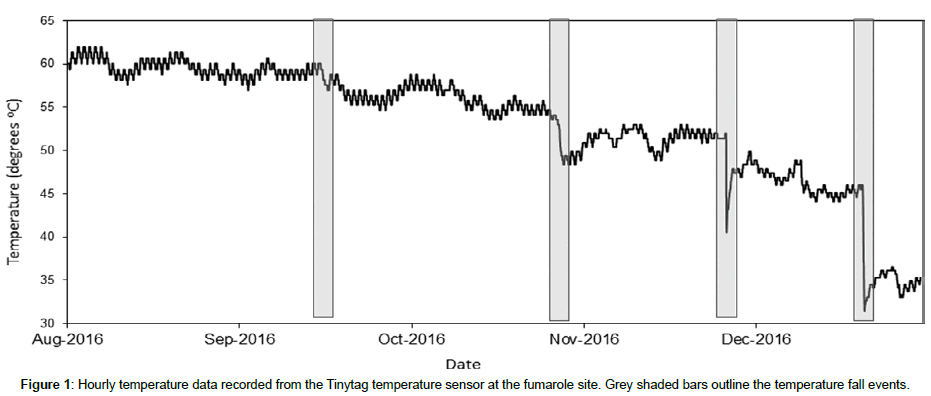
Hourly temperature time series data were derived from a Tinytag temperature sensor which has been installed at the surface of a fumarole site, buried approximately 20 cm under the surface of the volcano. The temperature data on the volcano have been measured from August 2016- January 2017 and 3571 records of hourly temperature data are plotted in Figure 1.
Kolmogorov-Zurbenko Filter
The decomposition of a time series is a necessary technique to determine the contribution of different frequencies to the data. The KZ filter provides effective separation of frequencies related to the long and short cycles. Different frequencies are uncorrelated and are related with different physical phenomena. Those phenomena are related to different components of the time series and they need to be separated to avoid interferences on the data [10-14].
The Kolmogorov-Zurbenko filter (KZ) filter has a simple design and provides the smallest level of interferences between the scales (long term component and short term component) of a time series [15]. It separates the long term variations from the short term variations in a time series which are related with the long and short cycles of the time series data. The KZ filter is also known to provide the best and closest results to the optimal mean square of error [15,16] and provides effective separation in data sets with missing observations [17,18]. Some examples of the use of the KZ filter are flood prediction in Schoharie Creek, New York; the prediction of ground level ozone in Albany, New York; and the explanation of water use time series in Gainesville, Florida [14,19-23].
The KZ filter is a low pass filter, defined by p repeated iterations of a simple moving average of m points. The moving average of the KZ filter is described by (Equation 1):
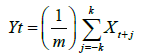 (1)
(1)
where m = 2k+1. The output of the first iteration becomes the input for the second iteration, and so on. The time series derived by p iterations of the filter, described in equation (1), is denoted by equation (2):
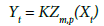 (2)
(2)
The parameter m in equation (2) has been determined to provide the separation of scales between the long and the short term cycles of the temperature time series and provides a physical explanation of the data.
In our study, a detrend transformation prior to a time series analysis was performed as temperature data were recorded during most of the second half of the year. Data were detrended to a stationary time series by computing the differences between consecutive observations. Using the difference operator, the raw temperature time series data can be expressed by the time series Tt given by the equation (3):
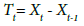 (3)
(3)
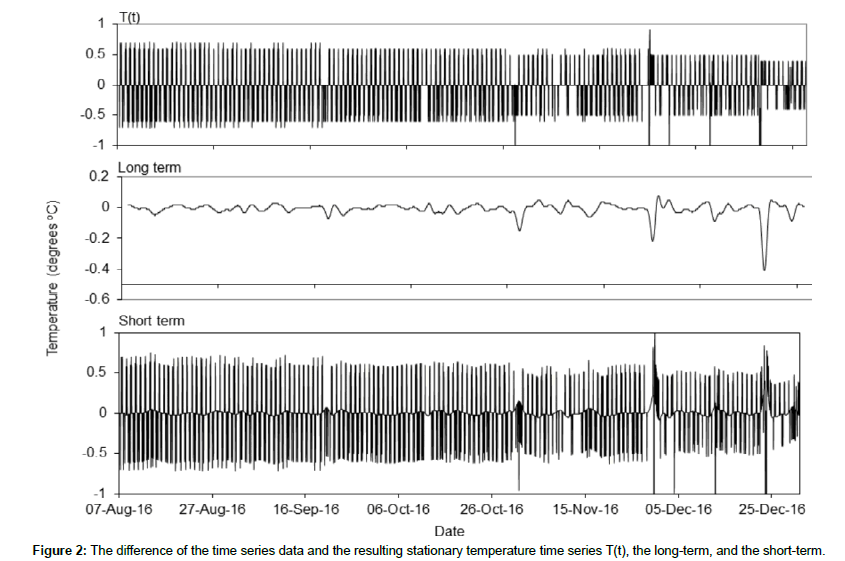
The difference of the time series data and the resulting stationary temperature time series T(t) is shown in the Figure 2. Difference temperature time series were separated into the long and short term components which are related with the long and short term cycles using the Kolmogorov-Zurbenko (KZ) filter [15]. For the decomposition of the time series we use the equation (4):
X(t) = L(t) + Sh(t) (4)
where X(t) represents the original time series of a variable, L(t) is the long-term trend component, and Sh(t) is the short-term component. The long-term component describes the fluctuations of a time series defined as being longer than a given threshold, while the short-term component describes the short-term variations. The long-term trend component consists of the trend component and the cyclical component [24]. The cyclical component of a time series is related with the fluctuations around the trend. The cyclical component can be viewed as those fluctuations in a time series which are longer than a given threshold, e.g. one and a half years, but shorter than those attributed to the trend. In most of the cases, we also study the seasonal component of the time series separately from the long- and short-term component. The seasonal component describes the cycles of year-to-year fluctuations. Since the temperature data in Nisyros volcano are measured for less than a year, we do not investigate the seasonal component in this study.
For our study, the temperature time series were decomposed to the long- and short-term variations, while the main periods on the data have been determined. The KZ filter has been applied to the difference of the temperature time series (T(t)) and reveals a time series without short-term variations and consisting only of the long-term variations of the time series (TKZ (t)). The difference of the temperature time series is shown by the equation (5):
T(t) = TKZ (t) + Tsh (t) (5)
A schematic representation of equation (5) is illustrated in Figure 2. The first graph shows the stationary temperature time series; the second graph is the long-term component which is devoid of short-term variations and the third graph represents the short-term component. With the long and the short term components of the temperature time series, we determine the main periodicities in R software using the kzft package.
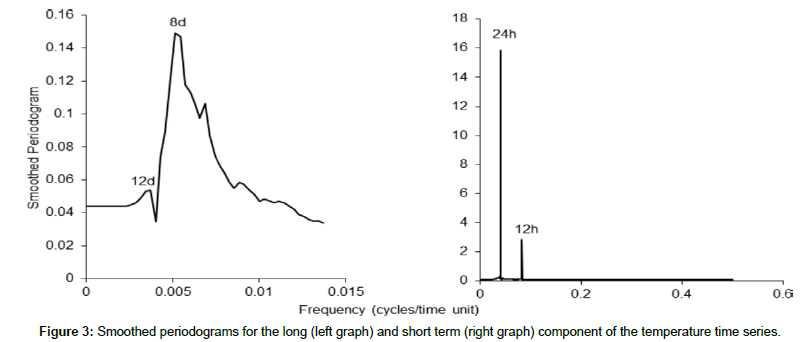
The periodograms for the long and short-term component of the temperature time series were smoothed with the DZ [25] algorithm in R software to identify the main periodicities and are shown in Figure 3.
To avoid the Nyquist effect of daily cycles in the temperature time series data (temperature is higher during the day and lower during the night), we decompose the time series data using the KZ filter with a threshold of more than 24 hours (1 day). Specifically, we decompose the time series into the long-term component (long-term cycles which are longer than a day) and a short-term component (shortterm cycles which are shorter than a day). For the decomposition of the time series, we use the KZ23,3 filter (length is 23 with 3 iterations) to provide a physically based explanation of the temperature time series data. Following a previously described methodology and parameters [19] for the KZ filter we provide the optimal solution to reveal the long and short cycles in the time series data. In particular, the parameters of the KZ filter have been estimated in order to reduce the short-term variations displayed in the long-term component of the time series.
Markov Chain
The Markov stochastic processes justify the conditional probability distribution of their future states relying on their present state. A discrete-time Markov process is referred as a Markov Chain (MC). An MC representation can break a time-series into sequences of segments, for example, time distances between identical temperature readings for our study, with specific properties (based on time series decomposition), and can be effective in domains where classic time series analysis has been used.
The Markov Chain process (MC) can be an effective methodology to better detect periodicities in short cycle events. MCs can have discrete sets of variables that can represent time in a number of different forms e.g. discrete or continuous and can reflect equivalently an MC state space. MCs representation can be via a form of directed graph although a graph and a transition matrix (that represents MC’s states) can also be independent of sequence.
MCs have been used successfully both for natural phenomena model simulation and simulation of precipitation events. MCs have been applied successfully in precipitation time series simulation [26], time-series using Monte Carlo algorithms [27] and general climate models [28], and urban drainage [29]. MCs provide an important element for present to future predictions in accordance with traditional past to present forecasting, thus they are important as a complementary approach to time-series analysis.
Markov chains describe a state t as a function of its previous value(s). The 1st order Markov model can be described by the equation (6):
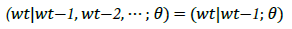 (6)
(6)
Equation 6 describes a probability density function where w at time t is dependent on the values of w at time t-1 given the parameter set θ [30].
MCs can be used on numbers or problems where short term horizon forecasting is required, and events can be simulated dynamically while domain situations develop. Additionally, advanced time-series can be generated, holding information on original time events and simulating phenomena that may take a substantial amount of time to gather.
In our study, while we have decomposed the time series data, an additional approach can be applied for the determination of the main periodicities. We apply MCs to describe the periodicity of time-series using the decomposition of the time series method as described in section 2.2. The period of a state t is denoted d(t) and it is the greatest common divisor (gcd) of those values of n where Ptn > 0. If the period is 1 then t is aperiodic. If the period is 2 or more then t is periodic.
Temperature data can belong to discrete continuous bands which are exhaustive and mutually exclusive. A temperature at any time can belong to only one band which can be regarded as a state since it is exhaustive and non-overlapping. In the 1st order Markov Chain process the relating probabilities of transitioning from state to state can be represented in a transition probability matrix. We had identified 56 distinct states represented by the equation (7):
T1, T2, …, T56 (7)
K-means Cluster Analysis
K-means clustering is a type of unsupervised learning in cluster analysis, which is used when you have unlabeled data (i.e., data without defined categories or groups). Cluster analysis is a technique for finding similarity of groups in a data, called clusters. It attempts to group individuals in a population together, but not driven by a specific purpose [31]. In K-means cluster analysis the main goal of the algorithm is to find groups in the data, with the number of groups represented by the variable K (K-clusters). The algorithm works iteratively to assign each data point to one of K groups based on the feature similarity. The new data can be labeled by the centroids of the K clusters.
Further advanced peak analysis has been performed on the MC periods using the K-means cluster analysis to identify the main periods in the long- and short-term components of the time series. We use three clusters for the long term component of the time series and the associated centroids were formed as described in Table 1. To determine the main periods in the long- and short-term component of the time series, the periods of the temperature values have been grouped to different clusters and they have been plotted against frequency in a histogram and the main clusters have been examined for each component, separately.
| Method | Periods (days) | |
|---|---|---|
| Long term | Short term | |
| Markov Chain | 3.5, 12.9, 25.4 | 0.5 |
| KZ Filter | 8, 12 | 0.5, 1 |
Table 1: Periods derived from the K-mean cluster analysis for the long and short term components using the KZ filter and the Markov Chain.
The possibility of transitioning across states can be described by a 56 × 56 matrix where each row represents a temperature band as measured from our Nisyros sensors and each column represents a band that each state can move into. Given our 148 day (147.8) measurements the transition matrix can be represented by the equation (8):
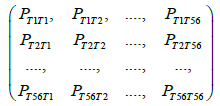 (8)
(8)
where PT1T1 is the probability that state T1, remains in the same state for (T1 +1) while PT1T2 is the probability for a temperature band to transition to state T2 for (T1 +1) and so on. Our focus was on the periodic effect of PT1T1, PT2T2, etc. in order to get an accurate frequency reading.
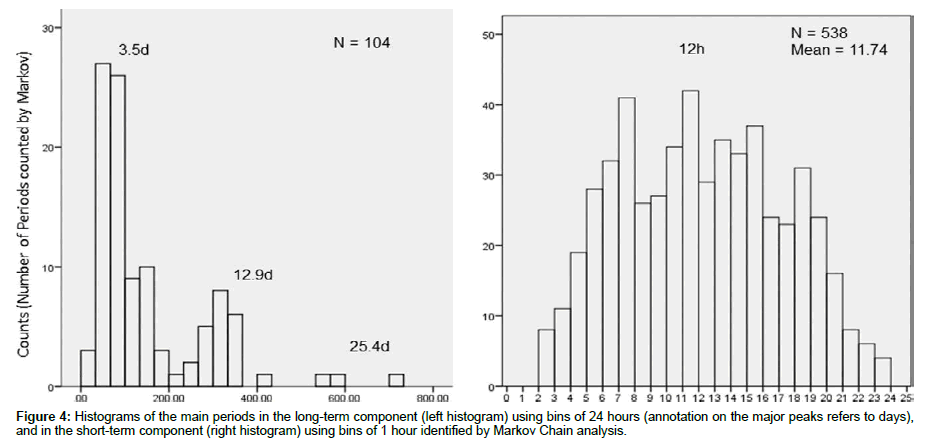
Major periods in the Markov Chain analysis were identified as the repeated time-distances between two successive identical temperature readings. We apply the first Markov order to count the time distances in hours between identical temperature readings among 3571 hourly temperature data in a linear manner. Histograms with bins of 24-hours were created to observe the major peaks of high frequency of time distances for the long- and short-term component of the time series, respectively. Markov Chain analysis of time distances below and above 24 hours yield the two major components of the long and the short terms in the time series data. Therefore, the decomposition of the Markov time distances has provided histograms of the major periods for the long- and short-term components (Figure 4).
Results
Data showed a descending trend ranging between 31.4°C and 62.0°C. There were 3572 hourly temperature measurements with no missing data. From the beginning of the last month of the summer until the middle winter season, measurements showed a decrease trend with subsequent cold temperature fall (CTF) at various time intervals (Figure 1). Sudden temperature falls initiated always at noon or few hours later between 12 and 4 pm the time intervals between those falls decreased as the winter season approached. From 42 day to 25 day time intervals the temperature falls increased from 2.4° C to 14° C. Temperature falls lasted 2 hours and sometimes for longer times such as 25 hours. A broad pattern showed longer times during the warmer temperatures, and shorter times during the colder temperatures.
In detail, on September 20th a small fall of the temperature lasted for 22 hours between 1:40 pm and 11:40 am after approximately 42 days, on October 31st another temperature fall of approximately 4°C started at 4:40 pm and lasted for 25 hours. A third temperature fall of 12.6°C occurred after 30 days on November 29th at 4:40 pm and lasted for 2 hours. The fourth temperature fall of 14°C happened after 25 days starting around 12:40 pm with duration of 7 hours.
Spectral Analysis
Using the KZ filter for the decomposition of the temperature time series, we determined the main periods in the spectral analysis domain. We applied the KZ25,3 filter on the detrending temperature time series data which was a stationary time series. Periodograms were determined for the long- and the short-term component of the time series, respectively (Figure 3). For the long-term component the main peaks, which corresponded to the main periodicities, were 8 days and 12 days. Both periods were related to cyclones that occur in the Aegean Sea which occur at periodicities from 4 to 12 days [32]. The remaining three peaks, which were not so sharp, corresponded to 3.5 days, 4.5 days, and 6 days. Those peaks were also related to possible tide and cyclone phenomena in the South Aegean Sea. The periodogram of the short-term component (Figure 3) showed the main peaks for the short term component of the time series to be 12 hours and 24 hours. The 12 hour period was the semi-period of 24 hours (daily cycles) of the temperature data. Thus, using the KZ filter for the decomposition of the time series, we determined that the main periodicity for the short-term component was the daily cycle (24 hours).
Markov Chain
Another approach to determine the main periodicities on the temperature data is the Markov Chain (MC). MC has shown numerous similar periods clustering around centers in a histogram (Figure 4) for the short-term and for the long-term components. K-means cluster analysis determined the main periods for both components where were three main peaks in the long-term component and one main peak in the short-term component (Table 1). For the long-term component, the centroids of the three clusters were a period of 3.5 days (n=48) and 12.9 days (n=23) (Table 1). There was also a minor period of 25.4 days (n=3). For the short-term component, there was one cluster in the histogram which showed that the main period is 0.5 day (12 hours). The 12-hour period was the semi-period of the daily cycle of the temperature data.
It is interesting that higher temperature readings occurred mostly during longer periods. The period of 3.5 days showed mostly temperature readings ranging from 33.0°C to 60.7°C, and the period of 12.9 days occurred within temperature readings ranging from 44.1°C and 61.4°C. The period of 25.4 days showed a range of temperature readings from 41.1°C to 48.4°C. The short-term component showed only one main period of 12 hours with all temperature readings. The hybrid model based on the KZ filter and the Markov Chain approach did not identify any larger periodicities, such as seasonal components. This is reasonable due to the limitation of the data which range over less than an annual cycle.
Discussion
Both methods, the Kolmogorov-Zurbenko filter (KZ) and the Markov-Chain (MC), are complementary tools for the elucidation of the main periodicities in the temperature data. The KZ filter is used for the time series decomposition of the temperature data into the long- and short-term components. MC results have been significantly improved by processing the decomposed data. This decomposition allowed MC to reveal shorter periodicities in the temperature data. Markov Chain may be used to prove probabilistically the periodicity in the temperature data and aggregate load impact in forecasting. The application of the time series decomposition in both techniques (KZ and MC) shows that the Kolmogorov-Zurbenko filter performs well in long cycles while the hybrid application of Markov Chain performs well in short cycles. The decomposition of a time series has shown that this is a necessary step to avoid the contribution of different frequencies to the data. The KZ filter provides an effective separation of frequencies related to the long and short periodicities.
The periods determined from our study are related to cyclones that occur in Aegean Sea or with the sea tides that occur around Nisyros Island. Since Nisyros is an island, the temperature measurement is reasonably affected by various phenomena (i.e. cyclones, sea tides) that occur in the sea. This methodology can be applied for the determination of the main periods in data at other locations, as well. With the decomposition of the time series and Markov Chain techniques, we can examine the volcanic temperatures at various volcanic sites. However, the periodicities of the temperature data will depend on the location and landscape of the volcano.
The atmospheric effect on a fumarole’s surface temperature log shows a periodicity from a few days to 12 days. Temperature falls are mostly related to mechanical triggering episodes rather than atmospheric changes which cause gradual temperature changes over days and occasionally within a day. A geological contribution is prominent in the raw data, however, it would be interesting to correlate decomposed continuous geochemical data collected hourly, which unfortunately are difficult to measure and currently do not exist.
Geological Interpretation of the Raw Data
In a volcanic island such as Nisyros is possible to affect the fumarole’s surface temperature through periodic impermeabilization via self-sealing of the argillic altered cover and embedded microfracture system. Nisyros is a result of volcanic and seismo-tectonic events including the manifestation of a series of volcanic phreatic eruptions mainly caused by the unstable operation of the upper hydrothermal system. Hydrothermal convection of meteoric water and seawater between the liquid-dominated zone and the vapordominated zone conveys heat and gases towards the surface. Any self-sealing as previously described [2] of the cover and the upper condensate zone will increase pressure while it will prevent heat release towards the fumarole’s surface. The first locations of temperature change on the volcano’s surface will be at fumarole sites which are the major manifestations of this young composite volcano’s activity on the Nisyros caldera surface. This study evaluates raw and decomposed temperature data and the associated periodicities of phenomena from the monitoring of a fumarole’s surface temperature at the caldera of the Nisyros volcano.
The decomposition of the temperature time series allows us to identify various other periodicities which may correspond to possible geochemical variables, geotectonic patterns and other phenomena. A decomposed temperature is separated from interferences from different physical phenomena, and this filtering process permits the identification of interferences from different physical phenomena in the raw temperature time series data which mask the real periodicities of those phenomena. Raw temperature data are records consisting all those interferences such as constructive noise or short-term variations. The decomposed temperature variable may be a significant indicator for observing the outgassing behavior from the upper level of a hydrothermal system and the monitoring of volcanic endogenic activity.
A fumarole’s surface temperature shows a series of temperature falls over a decreasing temperature trend during the downward semiannual atmospheric temperature cycle of the year. Those CTF events are visible in the raw temperature data with intermittent time intervals of stationary temperature time series ranging from 25 days to 42 days. Those intervals show an increasing frequency trend towards the winter season arrival, however, no long-term periodicity was identified by the KZ filter and hybrid MC application from the examined dataset for this time range. In addition, during this time of the year, although the South Aegean climate may experience some summer-temperature days there is no indication of any peak increase in the fumarole’s surface temperature implying another heat input other than the atmospheric temperature oscillation.
Temperature falls are followed by a gradual regain of the lost temperature implying another factor that impedes the heat transfer towards the surface. In detail, the series of the temperature falls recorded in the logger, after the stopping fall point are followed by a systematic rising trend and a leveling out at no more than half of the previous fall. At the beginning of a fall, a CTF occurs within a few degrees C which lasts for more than a day, while during the winter season the CTF occurs shortly for few to a couple of hours and within a fall of 14°C.
It is worth mentioning that the CTF events begin in the logger between 12:00 pm and 5:00 pm since those are cold temperature fall events it should be reasonable to expect them to be triggered during the coldest time of the day and not during the warmest time of a day. A time delay may exist between the times that a phenomenon impedes the convection of heat away from a heat source towards the surface and the surface temperature logger recording the drop in temperature.
We may assume that this is the time when the hydrothermal system pauses in its constant supply of thermal energy towards the surface. This is a lag time of 8-12 hrs prior to initiation of the CTF event. This can be the estimated travel time of the heat from the impedance zone (which could be a self-sealing layer or less clear pathways and fractures of the upper condensate zone of the hydrothermal system) to the surface. Since the main component that controls the heat transmission is the permeability, then this time interval denotes also the properties of the local permeability. If we consider the maximum depth of the impedance zone nearby the previously described impermeable layer [2] to be at the depth of 250 m, then it is reasonable to estimate a minimum speed of 250 m over 12 hours, that is 0.5 cm/sec (or a 1 ft/min) and a maximum speed of 0.8 cm/sec over the 8 hour delay.
The phenomenon that causes the CTF events (Figure 1) weakly appears at the end of the summer season, escalates through the autumn season and matures during the winter time indicating a higher frequency and a stronger effect showing with a deeper temperature fall. Although no measurements exist for the spring season, this can be a cyclical phenomenon strongly dependent on the downward trend of the annual temperature cycle. This phenomenon causing the CTF recorded by the temperature logger at the fumarole site may imply an episode of a reduced thermal energy release from the hydrothermal system or an inability of the hydrothermal system to release thermal energy towards the surface. Considering the latter case, it is possible that the hydrothermal system is adjusting its permeability. This permeability depends on clear pathways and fractures which may expand or shrink during the atmospheric seasonal variations and a threshold exists at which heat is unable to go through.
The CTF events may be dependent on the even longer term of the periodic phenomena derived from seasonal or global ocean or atmospheric tides or cyclones. However, a period requires a constant frequency of occurrences, and based on the various time intervals within the CTF events in the temperature raw data a strong relationship with atmospheric phenomena may not be the main cause.
Atmospheric seasonal variations may cause a gradual shrinking of the space hosting the volcanic gases as well as the volume of the volcanic gas itself. This process does not necessarily denote any physical variation of the entire hydrothermal system neither it excludes that reduced heat towards the surface was caused by impedance of the hydrothermal fracture system such as shrinking of the pathways. On the contrary, dilation or contraction of the hydrothermal fracture system may yield different rates of thermal emission towards the surface. In addition, during a CTF event the decreasing rate of the output thermal energy release from the upper condensate zone to the surface may be overwhelmed by the lack of atmospheric heat input during the winter time. Thus, a resulting significant colder temperature fall will be reflected in the temperature sensor.
Another important feature of the fumarole’s surface temperature data is that a little temperature fall takes place during the beginning of the autumn season and a dramatic temperature fall occurs during the middle of the winter season while there is an inverse relationship with the CTF operation time. Even though a more stable time lapse of the CTF events should occur as impermeabilization causes more permanent structures to hinder the degassing process nearby the surface, CTF events operate in ranges from a very short time of 2 hours to 25 hours. A CTF event occurs over longer times during the warmer (end of summer to beginning of autumn season) atmospheric temperatures and over shorter times during the colder temperatures (end of autumn season to middle of winter season). Assuming that degassing from the hydrothermal system is constant, then this CTF variable operation time may imply a seasonal effect of the atmospheric temperature on the stability of the impermeable layer or fracture system.
Considering the independence of the CTF events from the atmospheric seasonal effects and a constant degassing of the hydrothermal system, a self-sealing phenomenon would preserve the same periodicity by bringing aquifers, the fracture system, and the impermeable layer to a mechanical balance with respect to the confining burden providing constant periodic heat releases towards the surface. The hydrothermal system shows a temporal adjustment to seasonal atmospheric changes providing threshold points at which temperature drops suddenly and a CTF event happens. During this temporal change of the hydrothermal fracture system shrinking of the fractures and the porous space will take place. Local pressure and accumulation of thermal energy will exceed a threshold point at which fractures will again permit thermal energy to be released at the surface until the next shrinking event will yield a new temperature crisis. On the other hand, if we assume that Nisyros heat output from the hydrothermal system is not constant, then shortening of the operation time of the CTF events may imply an increase of heat output from the Nisyros hydrothermal system and a subsequent vulnerability of the Nisyros caldera surface stability.
The various frequency of the CTF does not exclude the impermeabilization process as one of the main driving mechanism of this phenomenon, but it is listed among others that would yield temperature falls strongly dependent on atmospheric temperature seasonality. Open fractures and porous space may permit more time for heat to go through and travel towards the surface during the summer time and less during the winter time. This assumption does not imply that more gas or energy is released during the summer time and less during the winter time as sensor measures only temperature. In addition this phenomenon probably causes an impermanent shrinking of the pathways and fractures that may momentarily shrink the porous space, fracture and pathway opening volume, impeding heat release towards the surface until accumulated heat will trigger the reopening of those and cessation of the CTF event. This phenomenon takes place in a cyclic way mostly dependent on atmospheric phenomena with the condition that heat output is constant from the hydrothermal system of Nisyros. This phenomenon would alleviate any normal heat accumulation nearby the surface and would preserve a favourable mechanical balance between the internal fluid pressure and the external atmospheric pressure avoiding triggering hydrothermal instability and further eruption. Periodicity of the CTF events may be considered as the threshold points at which the impedance of the hydrothermal system to release thermal energy is at peak and a temperature crisis occurs upon micro-fractures selfsealing. Studying the CTF periodicity may provide a useful early warning system prior to any risky volcanic activity.
Conclusion
For this study we analyzed raw and decomposed temperature data from a logger installed at the surface of a fumarole in Nisyros volcano. Raw data shows a variable frequency of temperature drops (CTFs) that may be related to geological phenomena while the decomposed data show constant frequencies and periodicities reflecting mostly atmospheric phenomena. The decomposition of a time series has shown that this is a necessary step to avoid interferences on the data. The hybrid model of the Kolmogorov-Zurbenko and the Markov Chain approach shows a complementary relationship that strengthens the identification of periodicities over a wide range of the long- and short-term components of the time series. The KZ filter shows an advantage for revealing the long-term processes while the Markov Chain may isolate the short-term processes. Short- and long-term periodicities of a fumarole’s surface temperature show evidence of a cyclic phenomenon with a mechanism that preserves a mechanical balance between the internal fluid pressure and the external atmospheric conditions, possibly through a cyclical operation of a micro-fracture system in an impermeable layer beneath the center of the Nisyros caldera surface. Studying the CTF periodicity may provide a significant signature of volcanic activity as CTF events and related temperature reading periods have shown that volcanic thermal energy is driven and regulated mostly by the atmospheric temperature variations in the Nisyros volcano. Using similar time series techniques for volcanic temperatures at other volcanic sites, we may reveal different periodicities depending on the geotectonic status of the volcano and explain geochemical and geophysical short-term oscillations reflecting various endogenic volcanic behaviors.
Acknowledgement
We are greatly acknowledging an anonymous referee for detailed comments and suggestions to improve the manuscript. Research was supported by Hofstra University. We are grateful for the help and cooperation received by the Mayor of Nisyros island and the hospitality provided, and the local people, especially Mr. Sideris Kontogiannis for his substantial assistance at the field.
References
- Martelli A (1917) Il gruppo eruttivo di Nisiro nel mare. Egeo Soc R Accademia dei Lincei, Italy.
- Fytikas M, Marinelli G (1976) Geology and geothermics of the Island of Milos (Greece). Proceedings of International Congress on Thermal Waters, Geothermal Energy and Volcanism of Mediterranean Area. Orense, Spain.
- Hedenquist JW, Henley RW (1985) Hydrothermal eruptions in the Waiotapu geothermal system, New Zealand; their origin, associated breccias, and relation to precious metal mineralization. Economic geology 80: 1640-1668.
- White DE (1955) Violent mud-volcano eruption of Lake City hot springs, northeastern California. Geological Society of America Bulletin 66: 1109-1130.
- Muffler LP, White DE, Truesdell AH (1971) Hydrothermal explosion craters in Yellowstone National Park. Geological Society of America Bulletin 82: 723-740.
- Keller J, Rehren T, Stadlbauer E (1990) Explosive volcanism in the Hellenic Arc: a summary and review. Proceedings of the Third International Conference Thera and the Aegean World III, Santorini, Greece.
- Geotermica Italiana (1984) Nisyros-2 geothermal well, Springer, USA.
- Lloyd EF (1959) The Hot Springs and Hydrothermal Eruptions of Waiotapu. Geol Geophys 2: 141-176.
- Marini LC, Principe G, Chiodini R, Cioni M, Fytikas, et al. (1993) Hydrothermal eruptions of Nisyros (Dodecanese, Greece). Past events and present hazard J Volcanol Geotherm Res 56: 71-94.
- Zurbenko IG, Sowizral M (1999) Resolution of the destructive effect of noise on linear regression of two time series. Far East J Theor Stat 3: 139-157.
- Tsakiri KG, Zurbenko IG (2008) Destructive effect of the noise in principal component analysis with application to ozone pollution. Proceedings of the Joint Statistical Meeting. Baltimore, Maryland, USA.
- Tsakiri KG, Zurbenko IG (2009) Model Prediction of Ambient Ozone Concentrations. Proceedings of the Joint Statistical Meeting, Baltimore, Maryland, USA.
- Tsakiri KG, Zurbenko IG (2011) Effect of noise in principal component analysis. Journal of Statistics and Mathematics 2: 37-40.
- Tsakiri KG, Zurbenko IG (2013) Explanation of fluctuations in water use time series. Environ Ecol Stat 20: 399-412.
- Zurbenko IG (1986) The Spectral Analysis of Time Series. (1st edtn) Elsevier Science & Technology, Academic Press, USA.
- Yang W, Zurbenko I (2010) Kolmogorov-Zurbenko filters. Computational Statistics 2: 340-351.
- Eskridge R, Ku JY, Trivikrama RS, Steven P, Zurbenko IG (1997) Separating Different Scales of Motion in Time Series of Meteorological Variables. Bull Am Meteorol Soc 78: 1473-1483.
- Yang W, Zurbenko I (2010) Non Stationarity. Computational Statistics 2: 107-115.
- Rao ST, Zurbenko IG, Neagu R, Porter PS, Ku JY, et al. (1997) Space and Time Scales in Ambient Ozone Data. Bull Am Meteorol Soc 1: 45-47.
- Rao ST, Zurbenko IG (1994) Detecting and Tracking Changes in Ozone Air Quality. Air Waste 44: 1089-1092.
- Hogrefe C, Rao ST, Zurbenko IG, Porter PS (2000) Interpreting the information in ozone observations and model predictions relevant to regulatory policies in the Eastern United States. Bull Am Meteorol Soc 81: 2083-2106.
- Tsakiri KG, Zurbenko IG (2010) Prediction of Ozone Concentrations using Atmospheric Variables. J Air Qual Atmosphere Health 4: 111-120.
- Tsakiri KG, Zurbenko IG (2010) Determining the main atmospheric factor on ozone concentrations. Meteorol Atmospheric Phys 109: 129-137.
- Data and Metadata Reporting and Presentation Handbook (2007) Organization for Economic Co-Operation and Development, India.
- Dirienzo AG, Zurbenko IG (1999) Semi-Adaptive nonparametric spectral estimation? J Comput Graph Stat 8: 41-59.
- Sørup HJD, Madsen H, Arnbjerg-Nielsen K (2012) Descriptive and predictive evaluation of high resolution Markov chain precipitation models. Environmetrics 23: 623-635.
- Negra NB, Holmstrøm O, Bak-Jensen B, Sørensen P (2008) Model of a synthetic wind speed time series generator. Wind Energy 11: 193-209.
- Gelati E, Christensen OB, Rasmussen PF, Rosbjerg D (2010) Downscaling atmospheric patterns to multi-site precipitation amounts in southern Scandinavia. Hydrol Res 41: 193.
- Sunyer MA, Madsen H, Rosbjerg D, Arnbjerg-Nielsen K (2017) Effects of climate model interdependency on the uncertainty quantification of extreme rainfall projections. Advanced Methods for Flood Estimation in a Variable and Changing Environment, Volos, Greece.
- Cinlar E (2013) Introduction to Stochastic Processes (1st edtn). Courier Corporation, USA.
- MacQueen JB (1967) Some Methods for classification and Analysis of Multivariate Observations. Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability: Statistics, University of California Press, USA.
- Alpar B, Yuce H (1996) Sea level variations in the eastern coasts of the Aegean Sea. Estuar Coast Shelf Sci 42: 509-521.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi