Research Article, Geoinfor Geostat An Overview Vol: 7 Issue: 1
Application of Geostatistical Techniques for the Determining of an Anomalous Zone of Copper Ore Deposit in the Area of Polkowice Mine (Region of Lubin-Sieroszowice, SW Part of Poland)
Barbara Namysłowska-Wilczyńska*
Wroclaw University of Science and Technology, Wroclaw, Poland
*Corresponding Author: Prof. Barbara Namysłowska-Wilczyńska
Wroclaw University of Science and Technology, Wroclaw, Poland
Tel: +48600035216
E-mail: Barbara.NamyslowskaWilczynska@pwr.edu.pl
Received: January 29, 2019 Accepted: February 18, 2019 Published: February 25, 2019
Citation: Namysłowska-Wilczyńska B (2019) Application of Geostatistical Techniques for the Determining of an Anomalous Zone of Copper Ore Deposit in the Area of Polkowice Mine (Region of Lubin-Sieroszowice, SW Part of Poland). Geoinfor Geostat: An Overview 7:1. doi: 10.4172/2327-4581.1000202
Abstract
This paper presents the results of investigations into the spatial variation of the principal geological parameters of strategic mineral resources, namely the copper ore deposits of Polkowice mine, occurring in the Lubin-Sieroszowice region (SW part of Poland). The studies were based on the data obtained by sampling of the Cu ore deposit with groove samples distributed mostly uniformly (at a spacing of 15-20 m) over the P-1 area of Polkowice mine. The studies concerned the Cu grade, thickness and quantity (accumulation) of the (recoverable) deposit concentrated in Whiteliegendes sandstones, Zechstein copper-bearing shales and calcareous-dolomitic formations. Selected geostatistical methods, i.e. ordinary kriging, bundled indicator kriging and conditional turning bands simulation have been used for the determining of an anomalous zones of Cu ore deposit.
In first stage of spatial studies ordinary (block) kriging for the estimation of the estimated averages Z* (with minimum variance of estimation σk 2) of deposit parameters within the P-1 block was used. Isotropic variograms were calculated and modelled by using of geostatistical models and then ordinary kriging was applied. Next, the indicator semivariograms for the following cutoff values of the studied parameters: Cu grade>1.7%, 2.2%, 2.7%; thickness>2.5
m, 3.0 m, 3.5 m and quantity>20[%mt/m2],>25 [%mt/m2],>30 [%mt/m2], were calculated. Probabilities P values in the block centres of the elementary grid, covering mining block P-1, were estimated by means of the bundled indicator kriging, taking into account the parameters of the indicator semivariograms models. As a result of the performed indicator estimations, the pictures of the probabilities P values distributions in raster maps of the exceeding of the assumed cutoffs were obtained.
In a successive stage of the analyses a conditional turning bands simulation technique was applied. The turning bands simulation was performed, taking into calculations of the theoretical models fitted to the Gaussian semivariograms of the deposit parameters. Statistical maps of the simulated values Zs distributions for quantity (mean of simulated values Zs, standard deviation of realizations σs, largest realization Zs, smallest realization Zs) and raster maps of probabilities P of exceeding of the assumed thresholds ( above cutoff values of quantity > 20[%mt/m2], >25[%mt/m2], > 30[%mt/m2] and below cutoff values < 20[%mt/m2], <25[%mt/m2], < 30[%mt/m2], were elaborated.
A comparison of the obtained results concerning used geostatistical techniques makes possible a better choice, indicating more useful and efficient method for estimating of mineral resources parameters and the determining of an anomalous zone of copper ore deposit.
Keywords: Copper ore deposits; Cu grade; Thickness; Quantity; Variation; Spatial analyses; Isotropic variogram; Indicator variogram; Gaussian variogram; Ordinary kriging; Bundled indicator kriging; Conditional turning bands simulation
Introduction
Geostatistics offers a wide range of different methodologies adapted to all raw materials and styles of deposits [1-24], including Zechstein sedimentary copper ore deposits occurring in the region of Lubin- Sieroszowice (SW part of Poland) [13-19,22,23] and porphyry copper deposit Rio Blanco, Peru [20]. The deposit structure of copperpolymettalic ores in the Foresudetic Monocline (region of Lubin- Sieroszowice) is of the stratified type [16,17].
Geostatistics is the most efficient framework to characterize, estimate and manage mineral resources [1,2,4-8,10,12,13-18, 23,24]. Needs relying in mapping, resource estimation, volume estimation and risk analysis appear for solving. Geologists or mining engineers can apply geostatistics at all stages of the mine life cycle, i.e. from exploration to development, production to site remediation. Applying geostatistics, one is obtained the large quality of evaluations at different stages of the development of projects.
Geostatistical methods are also efficient tools for optimizing reservoir characterization, providing the most efficient framework to build accurate and reliable static models of reservoirs (oil&gas), and valuable methodology at all steps of the geomodelling process. Besides mining, oil&gas and contaminated sites, geostatistics applies to air quality monitoring, subsurface modelling and natural hazards, biological resources, precision agriculture, not to mention other fields, such as geochemistry, epidemiology, meteorology, forestry, archeology, etc. [9,11]. Geostatistics provides efficient solutions for spatial data analysis, sampling optimization, 2D/3D mapping and risk assessment.
Risk analysis for mineral resource estimates generally relies on the use of conditional simulation, which, by characterizing spatial variability and producing multiple equi-probable realizations of the orebody, allows to characterize uncertainty (quantitative assessment of uncertainties) [3,5,7,17,19,21,22,24].
In this article, possibilities of different geostatistical methods as variogram function and ordinary kriging, bundle indicator kriging, as well as conditional turning bands simulation were presented [1,2,11,12,13-18,21-22,24]. The basis for the application of these techniques were: isotropic variogram (ordinary kriging) and indicator variogram (bundled indicator kriging) [1,3,5,10,11,16,17,21,22], while for the conditional turning bands simulation this basis constituted the Gaussian variogram [6,7,10,17,19,21,22,24]. Application of a such research approach permits for finding out, which among these techniques, which will be more suitable and effective for more detailed mapping the variation in the values of the deposit parameters: Cu grade, thickness, quantity, as well as, for the determining the probability of exceeding the assumed cut-off threshold (probability to be above cut-offs values and below cut-offs values), the determination of subareas with an anomalous mineralization with copper compounds, and also characterized by varying thickness and deposit quantity (accumulation) [16-18,21,22]. Obviously, the theoretical assumptions of used geostatistical techniques are quite different. Their application permitted for a comparing of the obtained results, i.e. deriving from the calculations connected with indicator estimation and simulation. These methods were used to achieve the same aim, using the same threshold values, showing accuracy and a quality of the developed spatial deposit models.
It was important to learn about general characteristics of the variation of deposit parameters within the post-exploitated P-1 block, carrying out the estimation with the use of ordinary block kriging.
A principal aim of spatial analyses was to identify the sub-areas with the highest probability P values, with assumed cutoffs values (thresholds), i.e. an anomalous zones of Cu ore deposit within the mining section P-1, using different approach (bundled indicator kriging, conditional turning bands simulation).
The results of the research were presented in the poster paper at the International Conference IAMG’2018, at the 19th Annual Conference of the International Association for Mathematical Geosciences, in Olomouc, Czech Republic (September 2-8,2018) [22].
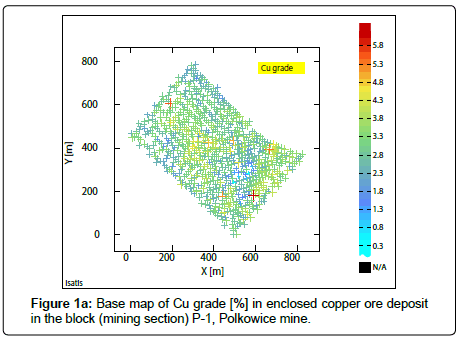
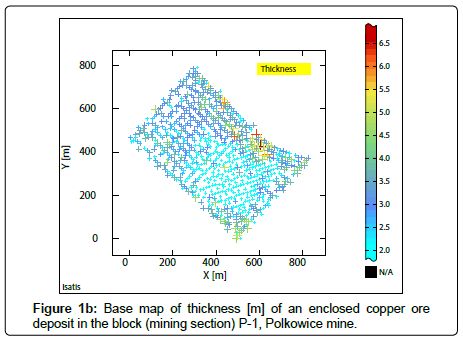
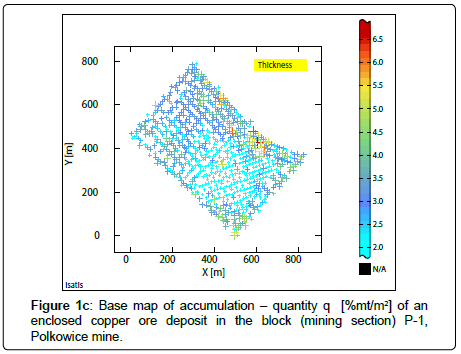
Spatial analyses were carried out for the deposit parameters: Cu grade, thickness and deposit quantity within the P-1 block of Polkowice mine (Figure 1a-1c), using the packet of geostatistical software Istatis (The geostatistical studies were conducted using geo-statistical software package ISATIS, version, 2017, Geovariances Firm, Avon-Cedex–Fontainebleau, France; www.geovariances.com) [8,9,11].The analyzed P-1 block is located in the middle area of the Polkowice mine. The depth ordinates of the P-1 block are contained between 810 m-840 m, below the surface area.
The Cu ore deposit is characterized by various lithological profiles of the copper-bearing series, occurring in the area of Polkowice mine. A copper mineralization comprises Whiteliegendes sandstones, boundary dolomite, copper-bearing shales and limestone-dolomite rocks of Zechstein. Among the principal copper minerals, chalcocite (Cu2S), bornite (Cu5FeS4), chalcopyrite (CuFeS2) and covellite (CuS) should be mentioned [16].
The weighted mean of Cu grade and the thicknesses for the individual lithological horizons as well as for whole deposit series when balance criteria are adopted (0.7% Cu), are included in the following ranges (Table 1A).
| Thickness | Cu grade | |
|---|---|---|
| Carbonate rocks (clay, streaked, limy - calcareous dolomites) | 2.20-4.00 m | 1.80-5.70% |
| Copper-bearing shales (clay, clay-dolomitic, dolomitic, tarry) | 0.15-0.45 m | 7.00-16.00% |
| Boundary dolomite | 0.01-0.05 m | 1.30-2.00% |
| Whiteliegendes sandstones | 0.20-2.00 m | 0.90-1.50% |
| Balanced deposit series (whole mineralized zone) | 2.86 m | 0.0302 |
Table 1A: The weighted mean of Cu grade and the thicknesses for the individual lithological horizons as well as for whole deposit series when balance criteria are adopted (0.7% Cu).
Starting from the floor of deposit series, towards roof, there occur successive varieties of dolomite: clay, streaked and limycalcareous. Whiteliegendes sandstones occur in the form of “islands” characterized by irregular superficial extent and shape. Apart from a full representation of the lithological profile of the deposit series, there are places where the mineralization includes only shales or shales and clay dolomite, or sandstone and shales.
Evaluation of principal statistics of deposit parameters
The results of calculations of principal statistical parameters values of the studied deposit parameters, i.e. copper grade, thickness and quantity have been shown in Table 1B.
| Deposit parameter | Size n | Minimal value Xmin | Maximal value Xmax | Mean Value  |
Standard deviation S | Variation coefficientV [%] |
|---|---|---|---|---|---|---|
| Cu grade [%] | 788 | 0.33 | 6.15 | 3.02 | 0.64 | 21 |
| Thickness [m] | 788 | 2.00 | 6.77 | 2.86 | 0.85 | 30 |
| Quantity [%mt/m2] | 788 | 1.62 | 41.55 | 20.83 | 6.08 | 29 |
Table 1B: A comparison of basic statistics of ledge parameters values for enclosed Cu ore deposit in block P-1 of Polkowice mine.
The lowest value of the coefficient of variation V was obtained for the Cu grade (V: 21%), as indicates still small variability located at the border - small and average limits of variation (Table 1B). A slightly greater average (moderate) variability is shown by thickness and accumulation (quantity) (V: 29-30%) (Table 1B). A degree of variation is comparable for both parameters.
Maximal value of Cu grade occurring in deposit series (enclosed) is connected with high concentrations of Cu compounds in copper-bearing shales and, in case of maximal value of deposit thickness, mainly with large thicknesses of mineralized carbonate rocks, a little bit with mineralized sandstones. The coefficient of linear correlation r, between Cu grade and thickness amounts to be -0.26 which indicates a negative correlation. Large thicknesses of deposit series are accompanied by low Cu grade and vice versa, low thicknesses are associated with rich concentrations of Cu compounds occurred in some parts of the P-1 block.
Research Methods
Spatial analyses of variation of the investigated deposit parameters, using different geostatistical methods, were carried out in successive stages, relying on estimation, indicator estimation and (conditional, non- conditional) simulation:
• Estimation
• Isotropic variogram modeling,
• Ordinary (block) kriging.
• Indicator estimation
• Indicator variogram modeling,
• Bundled indicator kriging,
• Conditional turning bands simulation
• Raw - Gaussian Anamorphosis,
• Gaussian variogram modeling,
• Simulation turning bands,
• Simulation Post-processing,
• Statistical simulation maps,
• Iso - cutoff maps of probability distribution.
Estimation
The basis of estimation conducted by means of using ordinary kriging procedure, were the parameters of the adopted theoretical models of isotropic variograms for deposit parameters (Table 2).
| Deposit parameter | Nugget effect | Partial sill variance | Total sill variance | Range of influence a | Basic model structures |
|---|---|---|---|---|---|
| C0 | C’ | C | [m] | ||
| Copper grade [%] | 0.1654 | 0.1031 | 0.4635 | 34.65 | nugget effect |
| 0.1949 | 145.95 | spherical | |||
| Thickness [m] | 0.3359 | 0.1108 | 184.6425 | 108.67 | nugget effect |
| 184.1958 | 3323.5 | spherical | |||
| Accumulation (quantity) [%mt/m2] | 13.659 | 11.6467 | 44.68 | 153 | nugget effect |
| 19.3743 | 377.4 | spherical |
Table 2: Modelling of isotropic semivariograms of deposit parameters.
Isotropic variograms
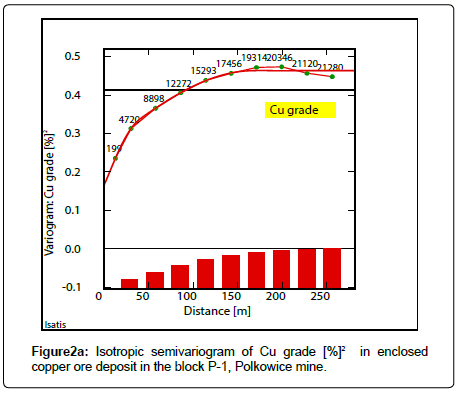
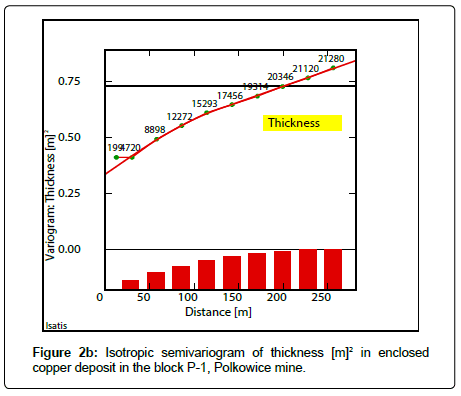
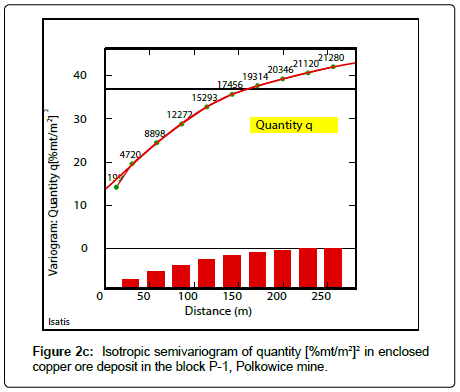
Isotropic semivariograms of the parameters: Cu grade (Figure 2a), thickness (Figure 2b), and quantity (accumulation) (Figure 2c), were calculated by applying of semivariogram function and subsequently modelled by means of assumed geostatistical models, mostly i.e. two spherical models combined with nugget effect C0 (Figure 2a to 2c). The results of isotropic semivariograms modelling of the analyzed deposit parameters have been presented in Table 2.
The obtained coefficients of correlation r between true values Z and estimated values Z* during performing the cross-validation procedure of conformity assessment of the adopted geostatistical models of variograms, using point ordinary kriging, are contained in the limits, from 0.491-0.708 (Cu grade: r - 0.491, average correlation; thickness: r - 0.655 and quantity: r – 0.708, very high correlation for both parameters; according to the classification of J. Guilford).
The semivariograms of deposit parameters show the nested nature of variation in their values, i.e. small scale (shorter range of influence a) and large scale variability (longer range of influence a), related to the analyzed parameters (Figure 2a to 2c). Small scale variations are particularly noticeable in the semivariogram of Cu grade (Table 2), can be traced at a distance amounting to twice the sampling interval (Figure 2a). In contrast, large-scale variability, especially in the case of the thickness of the deposit is observed (Table 2). The largest share of nugget effect C0 is observed in the semivariograms of Cu grade (Figure 2a) and the accumulation (Figure 2c). Shortest ranges of influence a occur in the semivariogram of Cu grade (Figure 2a).
Ordinary kriging
Kriging procedure predicts a value from a linear combination of surrounding data at any location. The criterion of minimizing the variance of the error between the estimated value Z* and the actual value Z leads to necessarily reducing the range of values Z*, compared to the actual range Z [1,10,13,16,17,24]. The more extreme values are not represented in the kriged estimates Z* (kriging smoothing effect), while they exist in reality and may have a significant impact on the deposit value [7].
Ordinary kriging procedure was used for evaluating of average values Z* with minimum variance of estimation σk2 within postmining block P-1 [16-18,23]. The block P-1 has been covered by elementary grid of block centers, N=3318: 42 (along X axis) × 79 (along Y axis). Mesh of this grid amounted to 17.5 m (along X) × 8.75 m (along Y).
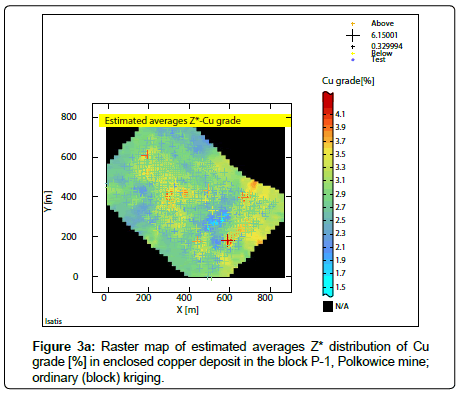
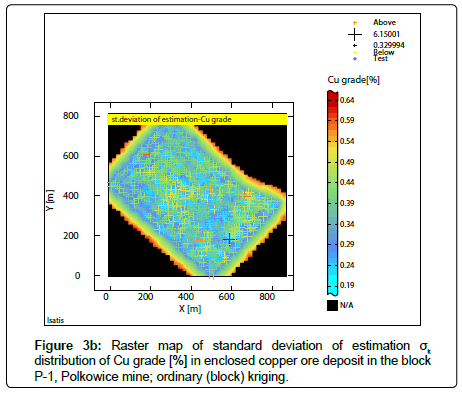
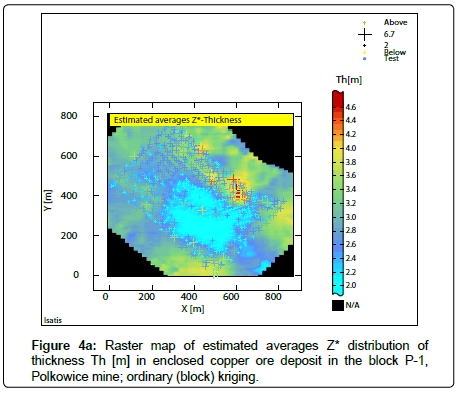
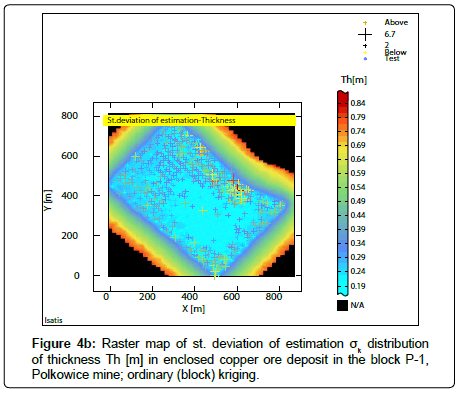
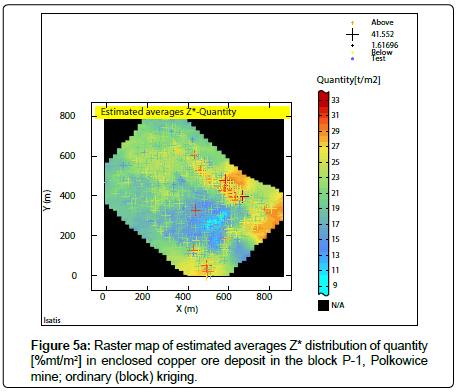
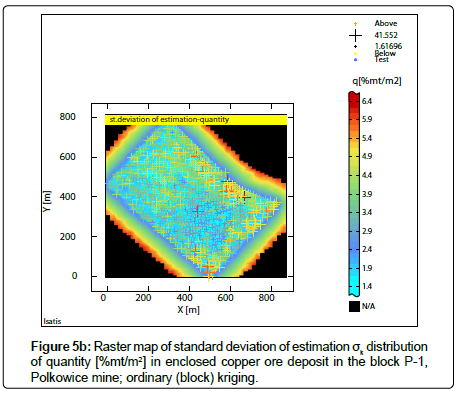
Estimated averages Z* and st. deviation of estimation σk of the parameters values were calculated, taking into kriging calculations the results of semivariograms modelling (Figure 2a-2c), using ordinary (block) kriging (Figures 3a-3b; 4a-4b; 5a-5b). Superficial distributions of averages Z* and standard deviation of estimation σk for the P-1 block have been presented in the raster maps (Figure 3a- 3b; 4a-4b; 5a-5b).
The results of the calculations of estimated averages Z* and standard deviation of estimation σk, carried out by means of ordinary kriging, have been shown in the Tables 3 to 5.
| Copper grade | Number of grid nodes N | Minimal value Xmin | Maximal value Xmax | Mean value  |
Standard deviation S | Variation coefficient V [%] |
|---|---|---|---|---|---|---|
| Estimated averages Z* [%] | 2355 788 | 1.55 0.33 | 4.29 6.15 | 2.99 3.02 | 0.38 0.64 | 13 21 |
| St. deviation of estimation sk [%] | 2355 | 0.19 | 0.64 | 0.33 | 0.12 | 37 |
Table 3: Global statistics of estimated values Z* of Cu grade [%] in enclosed Cu ore deposit in block P-1 of Polkowice mine; ordinary (block) kriging. The values of basic statistics of Cu grade parameter is given in italics.
| Thickness | Number of grid nodes N | Minimal value Xmin | Maximal value Xmax | Mean Value  |
Standard deviation S | Variation coefficient V[%] |
|---|---|---|---|---|---|---|
| Estimated averages Z* [m] | 3012 788 | 2.00 2.00 | 4.66 6.77 | 3.00 2.86 | 0.49 0.85 | 16 30 |
| St. deviation of estimation sk [m] | 3012 | 0.20 | 0.84 | 0.39 | 0.19 | 49 |
Table 4: Global statistics of estimated values Z* of thickness Th[m] in enclosed Cu ore deposit in block P-1 of Polkowice mine; ordinary (block) kriging. The values of basic statistics of thickness parameter is given in italics.
| Accumulation (Quantity) | Number of grid nodes N | Minimal value Xmin | Maximal value Xmax | Mean value  |
Standard deviation S | Variation coefficient V [%] |
|---|---|---|---|---|---|---|
| Estimated averages Z* [%mt/m2] | 2720 788 | 8.57 1.62 | 32.81 41.55 | 21.34 20.83 | 4.06 6.08 | 19 29 |
| St. deviation of estimation sk [%mt/m2] | 2720 | 1.47 | 6.34 | 2.83 | 1.47 | 52 |
Table 5: Global statistics of estimated values Z* of quantity [%mt/m2] in enclosed Cu ore deposit in block P-1 of Polkowice mine; ordinary (block) kriging. The values of basic statistics of accumulation (quantity) parameter parameters is given italics.
Size (n=788) of the studied subpopulation for the P-1 block is large and therefore a moving kriging neighborhood configuration has assumed, which can influence better for estimation quality. A moving neighborhood type: minimum number of samples=4 × number of horizontal angular sectors: 8 and optimum number of samples per sector=3, and so (4 × 8 × 3) has applied. A radius of search circle (kriging neighborhood) amounted to 80.5 m. A regular discretization point of elementary block 10 × 10 has taken in kriging calculations.
Linear interpolation technique like kriging gives an opportunity of obtaining of kriging variance σk2, a first measure of uncertainty [5,19]. The kriging variance σk2 is the variance of the error true value Z - estimated value Z*[16,17]. The square root of kriging variance σk2 for calculating a confidence interval for mean value  ,
, 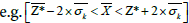 at the risk level of 5% has been using. This relies on the assumption that the error is symmetrical and Gaussian.
at the risk level of 5% has been using. This relies on the assumption that the error is symmetrical and Gaussian.
Uncertainty: A confidence interval for mean value  calculated on the basis of estimated averages Z* of Cu grade (Table 3):
calculated on the basis of estimated averages Z* of Cu grade (Table 3):
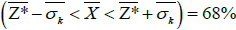
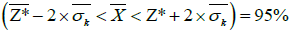
P(2.99-0.33< <2.99+0.33)=68%
<2.99+0.33)=68%
P(2.66<2.99<3.32)=68%
P(2.99 – 2 × 0.33< <2.99+2 × 0.33)=95%
<2.99+2 × 0.33)=95%
P(2.33<2.99<3.65)=95%
Uncertainty: A confidence interval for mean value  calculated on the basis of estimated averages Z* of thickness (Table 4):
calculated on the basis of estimated averages Z* of thickness (Table 4):
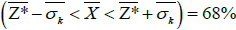
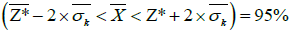
P(3.00 – 0.39< <3.00+0.39)=68%
<3.00+0.39)=68%
P(2.61<3.00<3.39)=68%
P(3.00 – 0.78< <3.00+0.78)=95%
<3.00+0.78)=95%
P(2.22<3.00<3.78)=95%
Uncertainty: A confidence interval for mean value  calculated on the basis of estimated averages Z* of accumulation (quantity) (Table 5):
calculated on the basis of estimated averages Z* of accumulation (quantity) (Table 5):
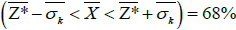
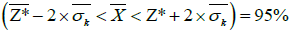
P(21.34 – 2.83< <21.34+2.83)=68%
<21.34+2.83)=68%
P(18.51<21.34<24.17)=68%
P(21.34 - 2 × 2.83< <21.34+2 × 2.83=95%
<21.34+2 × 2.83=95%
P(15.68<2<21.34<27.00=95%
The arithmetic mean  , evaluated on the basis of the estimated averages Z* (N=2355), for individual elementary blocks, is basically almost identical (Table 3), as the average
, evaluated on the basis of the estimated averages Z* (N=2355), for individual elementary blocks, is basically almost identical (Table 3), as the average  calculated using the original data Z (N=788) (Table 1). It concerns in particular to Cu grade (Table 3). Slight differences between these averages Z* are occurred, in case of remaining parameters (thickness, quantity) (Tables 4-5). Number of grid nodes N amounted suitably to 3012 (thickness) and 2720 (quantity).
calculated using the original data Z (N=788) (Table 1). It concerns in particular to Cu grade (Table 3). Slight differences between these averages Z* are occurred, in case of remaining parameters (thickness, quantity) (Tables 4-5). Number of grid nodes N amounted suitably to 3012 (thickness) and 2720 (quantity).
Coefficient V of the estimated averages Z* of Cu grade indicates small changes (V: 13%) of this parameter within block P-1 (Table 3). The V coefficient calculated on the basis of original values Z (V: 21%) is slightly higher, slightly exceeding the limit of low and moderate variability for this statistic (Table 1). In the case of other deposit parameters, the difference between the values of the V coefficient calculated for the averages Z* (N=3012, N=2720; Tables 4,5) and the original values Z (Table 1) is much bigger. The ranges of coefficients V of averages Z* are comparable for considered deposit parameters, a slightly lower for Cu grade (Tables 3-5). The coefficients V of averages Z* for thickness and accumulation (quantity) also prove of small variation in the values of both parameters (I group of variations) (Tables 4,5).
Coefficients V of standard deviation of estimation σk are much higher than the coefficients V of averages Z* for all investigated parameters, but the highest for quantity parameter (Tables 3-5).
The places with an increased concentration of Cu compounds and poor mineralization, sub-areas with larger and smaller mineralized series thicknesses and also with rich and poor quantity, can be traced in different raster maps of estimated averages Z* of the analyzed parameters (Figures 3a,5a).
The sub-areas were identified in raster maps of standard deviation of estimation σk of the studied parameters, where maps quality is poor, because of too much uncertainty and also rich, dense sampling grid (Figures 3b,5b). Coefficient V of standard deviation of estimation σk of Cu grade (Table 3) is much lower than values σk obtained for thickness and accumulation (Tables 4,5). The II group of moderate variation is related to Cu grade, while in the case of other parameters (thickness, accumulation), the III group of large variation can be observed.
Indicator estimation
Indicator kriging makes a non-parametric geostatistical technique [3,5,16,17,21,22], often applied, when data have been obtained as a result of sampling, characterizing by a positive skewness and sample population comprise outlier values, as is visible on histograms. Indicator kriging can be performed as ordinary kriging or simple kriging, by using indicator data. Selection of set of adequate cut-offs values (cutoffs), dividing original data of the investigated parameters into equal classes has been realized. Transformation of the set of original data into zero 0’ values and one 1’, with assuming of some cut-off values has been performed. Then interpolation of the ledge parameter values, separately for each class, has been conducted.
Indicator variograms
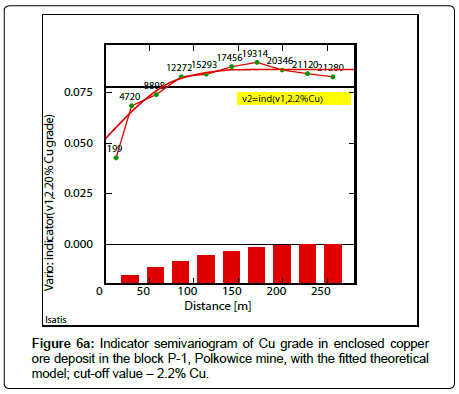
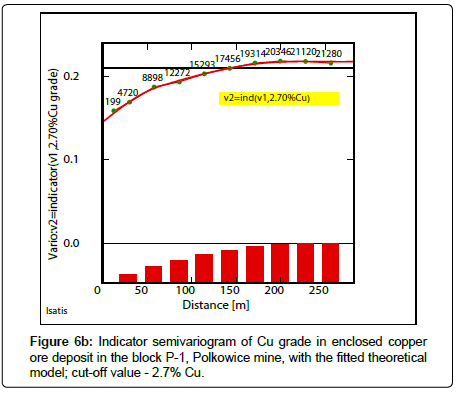
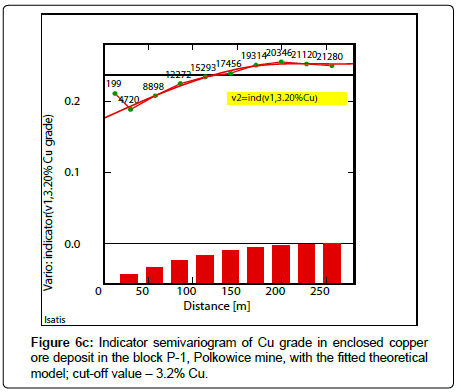
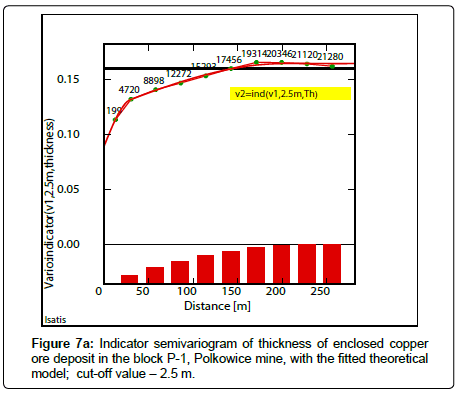
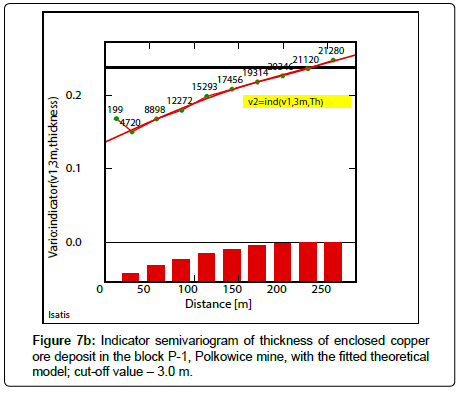
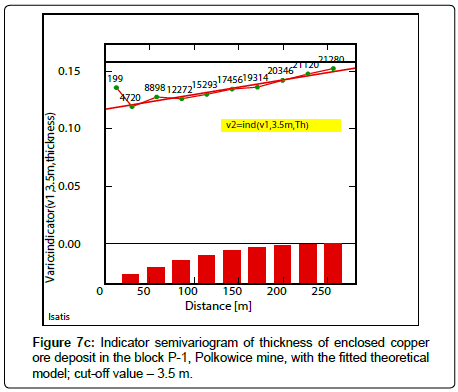
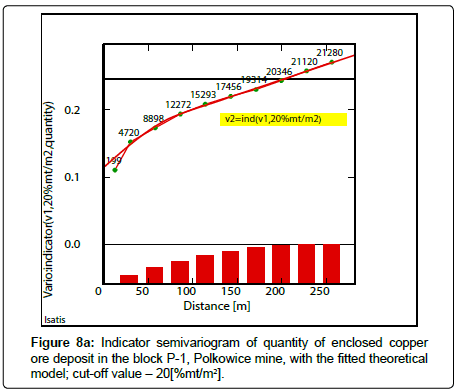
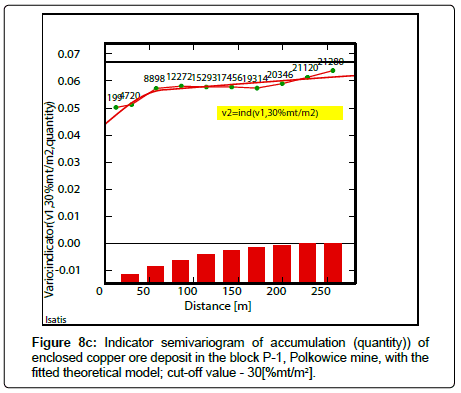
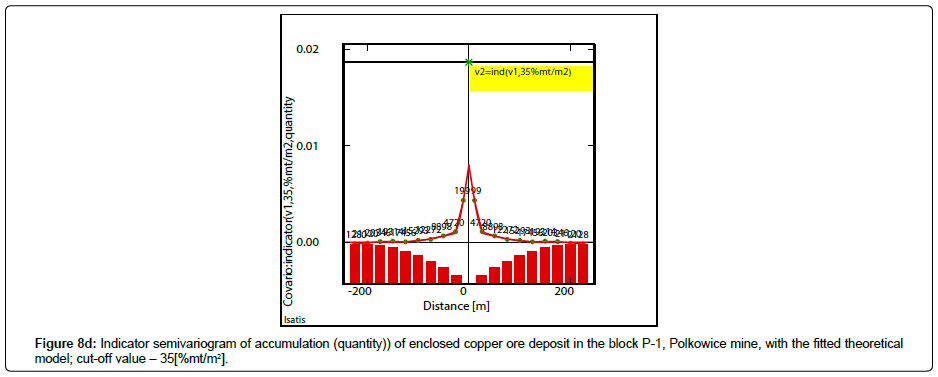
Indicator semivariograms have calculated by using indicator data, assuming different cutoff-values of the analyzed parameters. The assumed cutoff’s have been following: Cu grade-2.2% Cu (Figure 6a), 2.7% Cu (Figure 6b), 3.2% Cu (Figure 6c), thickness-2.5 m (Figure 7a), 3.0m (Figure 7b), 3.5m (Figure 7c) and quantity-20(%mt/ m2) (Figure 8a), 25(%mt/m2) (Figure 8b), 30(%mt/m2) (Figure 8c), 35(%mt/m2) (Figure 8d). Covariogram was calculated for this last cutoff value-35(%mt/m2), because of a decreasing trend of function Cov (h) values, together with distance (h) (Figure 8d).
Indicator semivariograms were modeled by means of combination of theoretical functions, i.e. a spherical model with nugget effect C0 or two spherical models with nugget effect C0 (Tables 6 to 8), in successive stage of the studies.
| Cu grade/ Cutoff value | Nugget effect C0 [%]2 | Partial sill variance C’ [%]2 | Total sill variance C [%]2 | Range of influence a [m] | Basic model structures |
|---|---|---|---|---|---|
| Cutoff value 2.2[%]Cu | 0.0518 | 0.0168 0.0177 | 0.0863 | 75.42 133.17 | nugget effect spherical spherical |
| Cutoff value 2.7[%]Cu | 0.1450 | 0.0197 0.0527 | 0.2174 | 53.90 187.25 | nugget effect spherical spherical |
| Cutoff value 3.2[%]Cu | 0.1764 | 0.0763 | 0.2527 | 178.67 | nugget effect spherical |
Table 6: A comparison of geostatistical models of indicator semivariograms of Cu grade in Cu ore deposit in block P-1 of Polkowice mine.
| Thickness/ Cutoff value | Nugget effect C0 [m2] | Partial sill variance C’ [m2] | Total sill variance C [m2] | Range of influence a [m] | Basic model structures |
|---|---|---|---|---|---|
| Cutoff value 2.5[m] | 0.1256 | 0.0239 | 0.3062 | 264.25 | nugget effect, spherical, spherical |
| 0.1567 | 418.77 | ||||
| Cutoff value 3.0[m] | 0.1364 | 0.0246 | 38.34793 | 171.4 | nugget effect, spherical, spherical |
| 38.1867 | 171063.6 | ||||
| Cutoff value 3.5[m] | 0.1169 | 31.7787 | 31.8956 | 373736 | nugget effect, spherical |
Table 7: A comparison of geostatistical models of indicator semivariograms of thickness of Cu ore deposit in block P-1 of Polkowice mine.
| Quantity/ Cutoff value | Nugget effect C0 [%mt/m2] | Partial sill variance C’ [%mt/m2] | Total sill variance C [%mt/m2] | Range of influence a [m] | Basic model structures |
|---|---|---|---|---|---|
| Cutoff value20[%mt/m2] | 0.1145 | 0.0412 113.1157 | 113.2714 | 75.425 333232.825 | nugget effect spherical, spherical |
| Cutoff value25[%mt/m2] | 0.1241 | 0.0188 0.5670 | 0.7100 | 107.80 6184.325 | nugget effect spherical, spherical |
| Cutoff value30[%mt/m2] | 0.0439 | 0.0110 0.0124 | 0.0673 | 56.70 620.90 | nugget effect spherical, spherical |
| Cutoff value35[%mt/m2] | 0.0106 | 0.0067 0.0012 | 0.0185 | 30.27 142.62 | nugget effect spherical, spherical |
Table 8: A comparison of geostatistical models of indicator semivariograms (covariograms) of quantity of Cu ore deposit in block P-1 of Polkowice mine.
The lowest value of the effect C0 can be related to indicator semivariogram determined for the lowest cutoff – 2.2% Cu (Figure 6a, Table 6). Higher value of the effect C0 can be observed in indicator semivariograms, calculated for bigger values of the cutoffs -2.7% Cu, 3.2% Cu (Figures 6b,6c, Table 6).
Longer ranges of influence a of indicator semivariograms of Cu grade and thickness, can be traced by assuming bigger values of cutoffs which correspond to large-scale variation (Tables 6,7). Comparable values of the effect C0 can be also observed in indicator semivariograms of thickness, slightly higher for biggest value of the cut-off -3.5 m (Table 7).
Comparable higher values of nugget effect C0 can be also observed in indicator semivariograms of quantity calculated for lower values of cutoffs, i.e. 20(%mt/m2) and 25(%mt/m2) (Figures 8a,8b; Table 8). Lowest values of effect C0 are connected with indicator semivariograms determined for biggest cutoff – 35(%mt/m2] (Figure 8c, Table 8). Ranges of influence “a” of indicator semivariograms are longer for lower cutoffs. Shorter ranges a and longer ranges a, can be interpreted by small-scale variation and large-scale variation of quantity.
Indicator semivariograms show small-scale variation and largescale variation of the studied parameters (Tables 6-8), similarly to isotropic semivariograms (Table 2).
Bundled indicator kriging
Bundled indicator kriging has been performing by using of indicator data (0, 1), according to the assumed cut-off values of the analyzed deposit parameters (given in Chapter 4.3.1) [5,17,21.22]. Ordinary kriging has been applied to estimate indicator data (0,1). Indicator kriging can be applied to the estimating of reserves of mineral resources, also in the studies of pollution of natural environment. Deposit reserves have been estimated by assuming of maximum risk, with the determining of confidence intervals [3,5,7].
Indicators solve a question of outlier values, because, during indicator estimation, the 1 values (or the 0 values) have been assigned to outlier values. The indicators given above or below cut-off value have been assumed during indicator estimation:
- the lowest cutoff value for Cu grade -2.2%; cutoff step value - 0.5% ; other cutoffs values for Cu grade - 2.7%, 3.2%;
- the lowest cutoff values for thickness-2.5 m; cutoff step value-0.5 m; other cutoffs values for thickness- 3.0 m, 3.5 m;
- the lowest cutoff value for accumulation– 20[%mtm2]; cutoff step value-5%mt/m2; other cutoffs values for quantity- 25[%mtm2], 30 [%mtm2], 35 [%mtm2].
A moving neighborhood type: minimum number of samples=4 × number of horizontal angular sectors=4 and optimum number of samples per sector=3 (4 × 8 × 3) has applied. A radius of search circle amounted to 80.5 m. A regular discretization 10 × 10 has assumed in indicator kriging calculations.
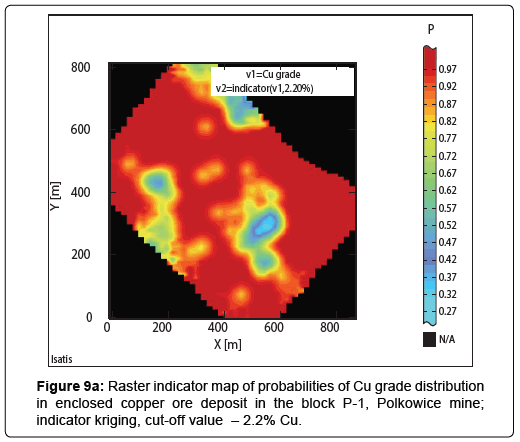
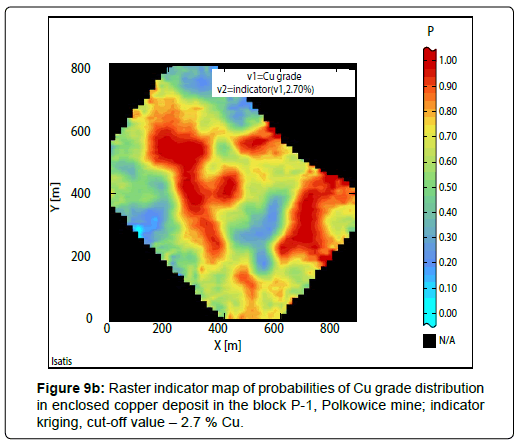
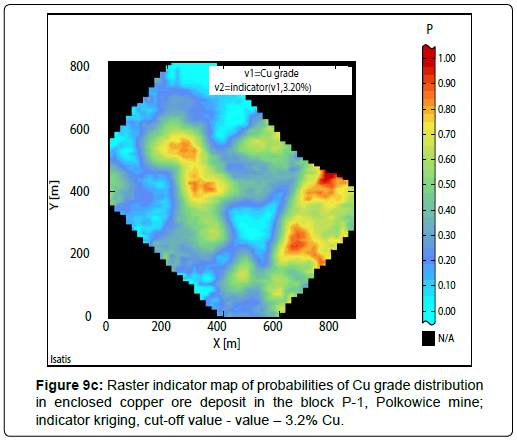
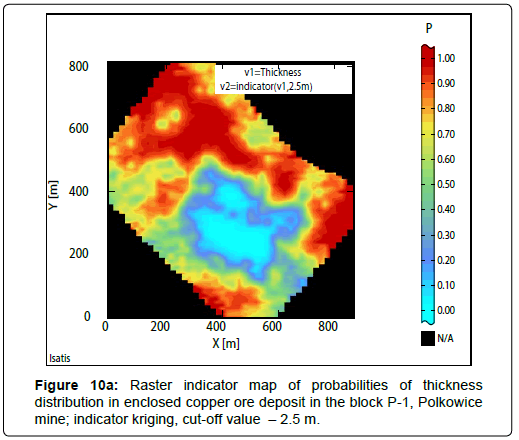
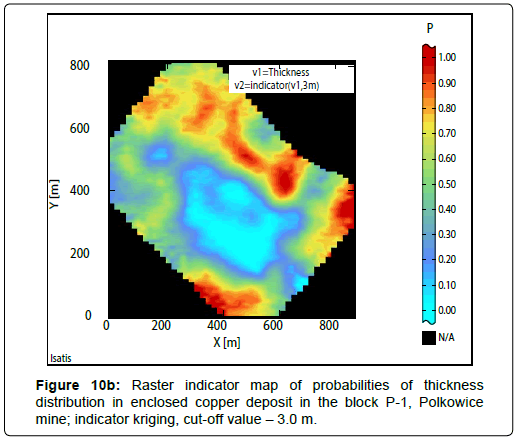
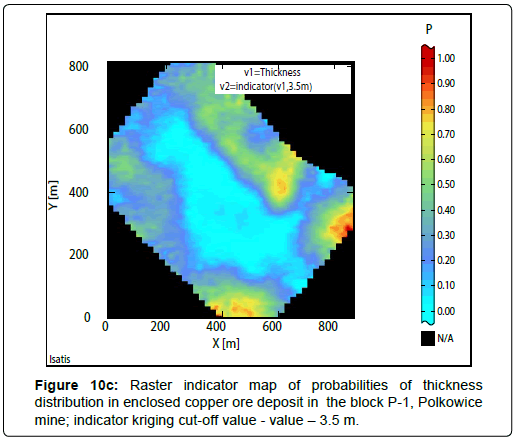
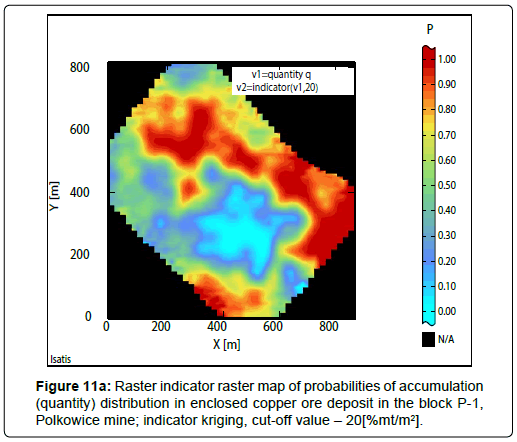
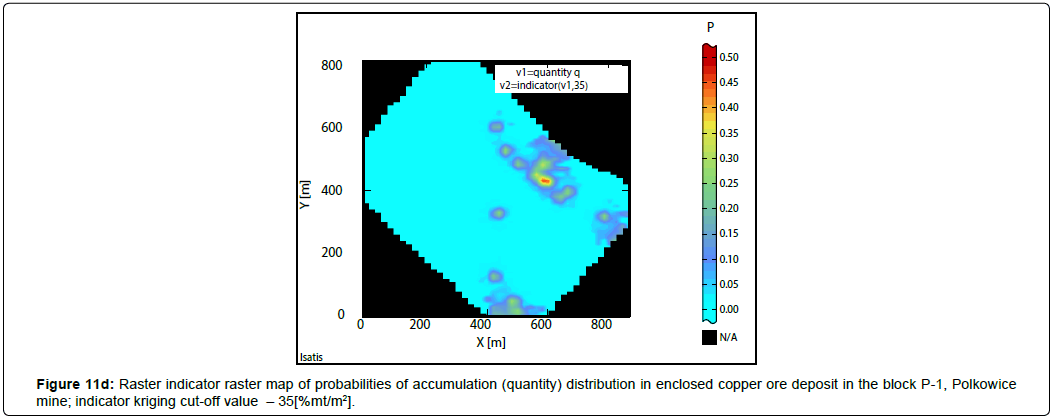
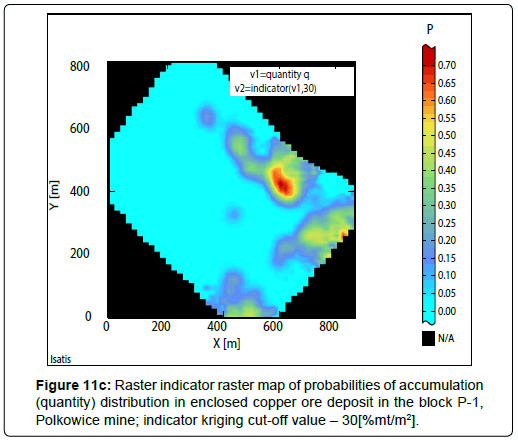
Results of indicator estimation: As a result of the indicator estimation by using of bundled indicator kriging, taking into calculations the parameters of indicator semivariograms models (Table 6), indicator raster maps with the block evaluations of probabilities P values, contained in the limits: 0 to 1, have been obtained (Cu grade-Figures 9a to 9c; thickness-Figures 10a to 10c; quantity-Figures 11a to 11d).
Indicator raster maps showing the results of calculations can be interpreted, as probability P, that the block value or the proportion of the block is situated above or below the assumed cut-off value (Figures 9a to 11d; Tables 9 to 11).
| Kriged indicator Cu grade | Number of grid nodes N | Minimal value Xmin | Maximal value Xmax | MeanValue  |
Standard deviation S | Variation coefficient V [%] |
|---|---|---|---|---|---|---|
| Cutoff 0.70 % Cu | 2355 | 0.91 | 1.00 | 1.00 | 0.01 | 1 |
| Cutoff 1.20 % Cu | 2355 | 0.80 | 1.00 | 1.00 | 0.02 | 2 |
| Cutoff 1.70 % Cu | 2355 | 0.64 | 1.00 | 0.99 | 0.04 | 4 |
| Cutoff 2.20 % Cu | 2355 | 0.30 | 1.00 | 0.92 | 0.12 | 13 |
| Cutoff 2.70 % Cu | 2355 | 0.00 | 1.00 | 0.67 | 0.21 | 31 |
| Cutoff 3.20%Cu | 2355 | 0.00 | 1.00 | 0.37 | 0.24 | 64 |
Table 9: Global statistics of kriged indicator values (probability P) of Cu grade [%] in enclosed Cu ore deposit in block P-1 of Polkowice mine; bundle indicator kriging.
| Kriged indicator Thickness | Number of grid nodes N | Minimal value Xmin | Maximal value Xmax | Mean value  |
Standard deviation S | Variation coefficient V [%] |
|---|---|---|---|---|---|---|
| Cutoff 2.00 m | 2355 | 1.00 | 1.00 | 1.00 | 0.00 | 0.00 |
| Cutoff 2.50 m | 2355 | 0.00 | 1.00 | 0.66 | 0.29 | 44 |
| Cutoff 3.00 m | 2355 | 0.00 | 1.00 | 0.50 | 0.27 | 55 |
| Cutoff 3.50 m | 2355 | 0.00 | 1.00 | 0.27 | 0.21 | 78 |
| Cutoff 4.00 m | 2355 | 0.00 | 0.73 | 0.11 | 0.14 | 124 |
Table 10: Global statistics of kriged indicator values (probability P) - thickness [m] in enclosed Cu ore deposit in block P-1 of Polkowice mine; bundle indicator kriging
| Kriged indicator Quantity | Number of grid nodes N | Minimal value Xmin | Maximal value Xmax | Mean value  |
Standard deviation S | Variation coefficient V [%] |
|---|---|---|---|---|---|---|
| Cutoff 20[%mt/m2] | 2355 | 0.00 | 1.00 | 0.60 | 0.31 | 52 |
| Cutoff 25[%mt/m2] | 2355 | 0.00 | 1.00 | 0.26 | 0.26 | 103 |
| Cutoff 30[%mt/m2] | 2355 | 0.00 | 0.88 | 0.07 | 0.15 | 197 |
| Cutoff 35[%mt/m2] | 2355 | 0.00 | 0.48 | 0.02 | 0.05 | 287 |
Table 11: Global statistics of kriged indicator values (probability P) - quantity[%mt/m2] in enclosed Cu ore deposit in block P-1 of Polkowice mine; bundle indicator kriging.
When the cutoff value of 2.2% Cu was assumed during the indicator estimation, almost in the whole area of the P-1 block, the sub-areas with the highest probability P values prevail, within the limits from: 0.92-0.97 (Fig. 9a) (Table 9). Their dimensions decrease significantly when the cut-off value will be increased to 2.7% Cu, while the largest P values are ranged, between 0.9-1.00 and 0.70-0.90 (Figure 9b). In raster map calculated for the highest cut-off value - 3.2% Cu, it can be noticed much smaller sub-areas with the biggest values of probability P (Figure 9c).
Uncertainty: Probability intervals for mean  calculated on the basis of indicator values Z* for Cu grade:
calculated on the basis of indicator values Z* for Cu grade:
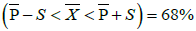
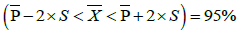
Cutoff - 2.2% Cu
P(0.92 – 0.12< <0.92+0.12)=68%
<0.92+0.12)=68%
P(0.80<0.92<1.04)=68%
P(0.92- 2 × 0.12< <0.92+2 × 0.12)=95%
<0.92+2 × 0.12)=95%
P(0.68<0.92<1.16)=95%
Cutoff - 2.7% Cu
P(0.67 – 0.21< <0.67+0.21)=68%
<0.67+0.21)=68%
P(0.46<0.67<0.88)=68%
P(0.67- 2 × 0.21< <0.67+2 × 0.21)=95%
<0.67+2 × 0.21)=95%
P(0.45<0.67<1.09)=95%
Cutoff -3.2% Cu
P(0.37 – 0.21< <0.37+0.21)=68%
<0.37+0.21)=68%
P(0.16<0.37<0.58)=68%
P(0.37- 2 × 0.21< <0.37+2 × 0.21)=95%
<0.37+2 × 0.21)=95%
P(-0.05<0.37<0.79)=95%
The strongest confidence levels can be noticed for the cutoff of Cu grade, amounting to 2.2% Cu.
Large subareas with probability P values, varied between 0.90 and 1.00 occur, by assuming the cutoff value -2.5 m are observed in the indicator map of thickness (Figure 10a) (Table 10). The dimensions of these surfaces have become much smaller, if the cutoff value to 3.0 m has been increased, then the P values are contained within the ranges varying from 0.70-0.80, 080-0.90, 0.90-1.00 (Figure 10b). However, if the cutoff value reaches the value of 3.5 m, the areas with the highest P values: 0.80- 0.90, 0.90-1.00, constitute extremely small enclaves (Figure 10c).
Uncertainty: Probability intervals for mean  calculated on the basis of indicator values Z* of thickness:
calculated on the basis of indicator values Z* of thickness:
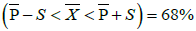
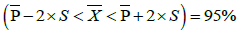
Cutoff - 2.5 m
P(0.66 – 0.29< <0.66+0.29)=68%
<0.66+0.29)=68%
P(0.37<0.66<0.95)=68%
P(0.66 - 2 × 0.29< <0.66+2 × 0.29)=95%
<0.66+2 × 0.29)=95%
P(0.08<0.66<1.24)=95%
Cutoff - 3.0 m
P(0.50 – 0.27< <0.50+0.27)=68%
<0.50+0.27)=68%
P(0.23<0.50<0.77)=68%
P(0.50 - 2 × 0.27< <0.50+2 × 0.27)=95%
<0.50+2 × 0.27)=95%
P(-0.04<0.50<1.04)=95%
Cutoff - 3.5 m
P(0.27 – 0.21< <0.27+0.21)=68%
<0.27+0.21)=68%
P(0.06<0.27<0.48)=68%
P(0.27 - 2 × 0.21< <0.27+2 × 0.21)=95%
<0.27+2 × 0.21)=95%
P(-0.15<0.27<0.69)=95%
The strongest confidence level can be noticed for the cutoff of thickness, amounting to 2.5 m.
The largest subareas with P values contained, within the limits of 0.9-1.00 and 0.80-0.90 (Figure 11a) are observed in indicator map, calculated for the threshold value – 20(%mt/m2) (Table 11). The surface dimensions begin to significantly decrease, with the increasing of the threshold value to 25(%mt/m2). The probabilities P are ranged within the limits, P: 0.70- 0.80, 0.80- 0.90 and 0.90- 1.00 (Figure 11b). Sub-area with highest P values (0.90-1.00) shows small surface (Figure 11b).
When the threshold values are assumed, respectively up to 30(%mt/m2) and 35(%mt/m2), the subareas with the highest values P (P: 0.55-0.65, 0.65- 0.70) are strongly reduced, until they become quite small enclaves, P: 0.35-0.40 and 0.40- 0.50 (Fig. 11c ÷11d) (Table 11).
Uncertainty: Probability intervals for mean  calculated on the basis of indicator values Z* of quantity:
calculated on the basis of indicator values Z* of quantity:
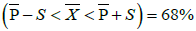
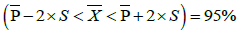
Cutoff – 20[%mt/m2]
P(0.60 – 0.31< <0.60+0.31)=68%
<0.60+0.31)=68%
P(0.29<0.60<0.91)=68%
P(0.60 - 2 × 0.31< <0.60+2 × 0.31)=95%
<0.60+2 × 0.31)=95%
P(-0.02<0.60<1.21)=95%
The biggest confidence level can be noticed for the cutoff of quantity, amounting to 20[%mt/m2].
Conditional turning bands simulation
The use of simulation models has been performed to study the nature of certain phenomena.
Simulation is preferred over kriging when a model of the spatial fluctuations is more important than accuracy at the local scale. For a given sample at any non-sampled location the conditional simulation variance is larger than the kriging variance at the same location [3,5-7,10,11,17,19,21,22]. In geostatistics usage of simulation, is restricted to synthetic realizations of a random function that possesses the same spatial statistics as the actual realization, as measured by moments up to order 2. While a kriging surface is unique, there are an infinite number of simulated surfaces for the same data and statistical moments. Conditional simulations allow generating many realizations of a random function conditioned to actual data for reproducing its statistical distribution and its spatial correlation (e.g. variogram). Conditional simulation of a single random function honors the sample values, however non-conditional simulation doesn’t honor the data.
Procedures used in the conditional simulation of regionalized variables include, among others, the turning bands method or indirectly by this method. The latter process combines three random functions and uses two sets of known values to force the simulation to honor the data.
Let Z*(x0) be a kriging estimate at location xO of a regionalized variable defined over the n-dimensional Euclidean space Rn, modeled by the random function Z(x). This estimate is based on a set of m observations Z(xi). Let Z1(x0) be a single realization of an nonconditional simulation of Z(x) produced by the turning bands method using the same original data. Let Z2(x0) be a kriging estimate of Z(x0) calculated from a realization of an non-conditional simulation of Z(x) produced by the turning bands method at the same locations xi as the original data set. A realization Z3(x0) of the conditional simulation of Z(x) at x0 is given by: Z3(x0)=Z*(x0)+Z1(x0) Z2(x0).
Turning bands is a space transformation of the second kind used for numerical simulation of n-dimensional realizations of a random function. The n-dimensional realizations are obtained by adding the contributions of several independent 1-dimensional realizations along lines, which are randomly or uniformly distributed in a Euclidean space. This method produces realizations multi-normally distributed (central limit theorem), but doesn’t directly produce a conditional simulation.
In practical applications one must sometimes simulate realizations of a given random function in R2 or R3 for the stationary random function (SRF), as well as for the intrinsic random function (k-IRF).
If an isotropic covariance Cn on Rn is given, the “turning bands” method will yield a realization of a SRF a stationary random function with covariance Cn, if it is applied to a realization of SRF Y with the corresponding covariance C1 on R1. The turning bands method may also be used in order to construct representations of a k-IRF with a given isotropic generalized covariance (GC) on Rn.
Geostatistical conditional simulations make possible to deliver models that accurately represent the actual distribution and spatial variability of the studied variables. Applying cut-offs on a simulated block model is a correct approach, particularly if the criterion is a complex and non-linear transform of several grade elements. Moreover by generating many simulations, each being considered as a acceptable (credible) “reality”, this allows you to be able to have an access for a characterization of uncertainty that can lead to the producing of E-type estimates.
For scenario reduction simulation offers a quick way to identify grade realizations which best represent the whole space of uncertainty. The selected scenarios can be readily implemented to characterizing the risk attached to a project due to the uncertainty on the resource for:
• Open pit optimization and mine scheduling;
• Evaluation of projects when taking financial and technical uncertainties into account;
• Mine optimization for a portfolio of deposits.
• Conditional simulation can also be used for:
• Recoverable resource estimation,
• Characterization the precision of recoverable estimates,.
• Sampling optimization,
• Resource classification.
The probabilistic framework of the geostatistical model underlying the generation of simulations, permits to carry out risk analysis. Risk analysis for mineral resource estimating generally relies on the use of conditional simulation. Conditional simulation, by characterizing spatial variability and producing multiple equi-probable realizations of the orebody, allows you to characterize uncertainty.
Conditional simulation makes possible to realize:
• Quantitative assessment of uncertainties;
• Production of probability based indicators and probability (indicator) maps;
• Supporting Monte Carlo risk analysis;
• Reproducing the orebody heterogeneities,
• Capturing and reducing the space of uncertainty via scenario reduction, allowing effective multiple scenario analysis.
Uncertainty usually following any geostatistical study, in which case it is related to the risk of making an incorrect decision, because the estimates don’t agree with reality [5,7,10,17,19,24]. This parameter - uncertainty is often measured by parameters such as confidence intervals, probability intervals and standard errors. Standard error is the standard deviation of the difference between an actual parameter and its estimate for an estimator, without bias.
Raw - Gaussian Anamorphosis
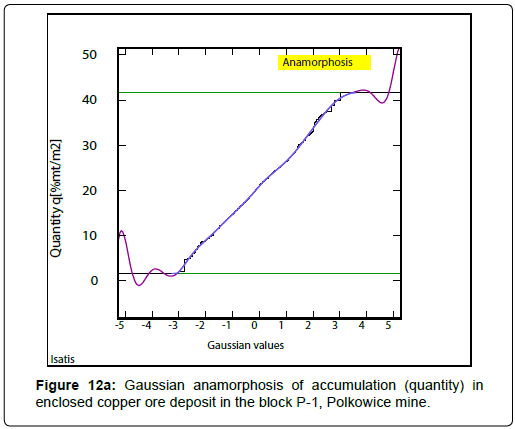
The values of Cu grade, thickness and deposit accumulation (quantity) were transformed into Gaussian values. The results of Gaussian transform were shown only for quantity.
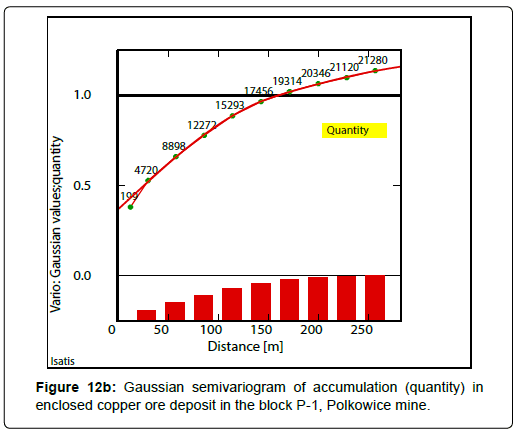
It was performed Gaussian transform (point anamorphosis) (Figure 12a) and Gaussian semivariogram of quantity was calculated on the basis of Gaussian values (Figure 12b).
Gaussian variogram modelling
Gaussian semivariogram of quantity was modeled by means of theoretical functions, i.e. two spherical models with nugget effect (Table 12).
| Parameter - Accumulation (Quantity) | Number of of grid nodes N | Minimal value Xmin | Maximal value Xmax | Mean value | Standard deviation S | Variation coefficient V [%] |
|---|---|---|---|---|---|---|
| Mean of realizations Zs [%mt/m2] | 3608 | 9.43 | 31.96 | 21.82 | 3.9 | 18 |
| St. deviation of realizations ss [%mt/m2] | 3608 | 1.25 | 8.59 | 3.88 | 2.27 | 58 |
| Smallest realization Zs [%mt/m2] | 3608 | 1.62 | 27.61 | 12.26 | 5.89 | 48 |
| Largest realization Zs [%mt/m2] | 3608 | 13.1 | 41.55 | 31.27 | 7.09 | 23 |
Table 12: A comparison of geostatistical models of Gaussian semivariogram of quantity parameter for Cu ore deposit in block P-1 of Polkowice mine.
A significant share of nugget effect C0 is observed in the course of Gaussian semivariogram of accumulation (quantity) (Figure 12b). The course of Gaussian semivariogram of accumulation indicates a nested nature of variation in values of this parameter, i.e. small scale (shorter range of influence a) and large scale of variability (longer range of influence a) (Table 12).
Calculations connected with conditional simulation turning bands
It was assumed that the number of the carried out simulations and the number turning bands have amounted respectively to 100 and 2000. A moving neighborhood type (4 × 8 × 3): minimum number of samples=4 × number of horizontal angular sectors=4 and optimum number of samples per sector=3 has applied. A radius of search circle amounted to 80.5 m. A regular discretization of 10 × 10 has been taken in calculations connected with turning bands (nonconditional and conditional) simulation.
Simulation Post-processing
The results of the conducted calculations connected with turning bands simulation have been contained in the Simulated Macro-Variable for analyzed Gaussian variables and then have been subjected Simulation Post-Processing.
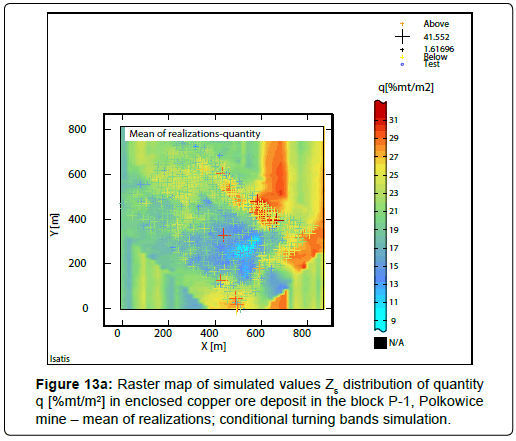
Raster statistical maps of simulated values Zs and iso-cutoff values maps were calculated for the quantity and shown in the Figures 13a.
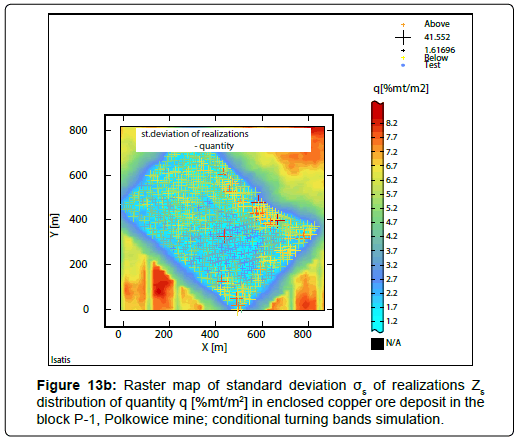
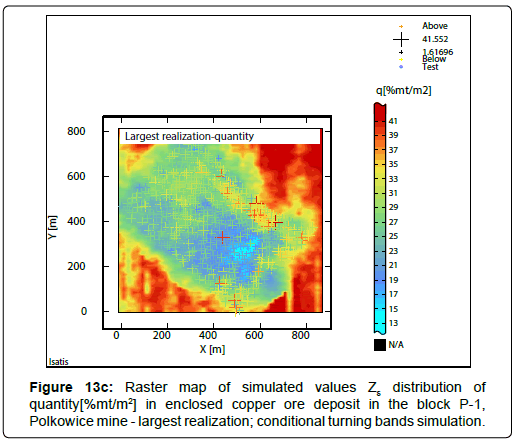
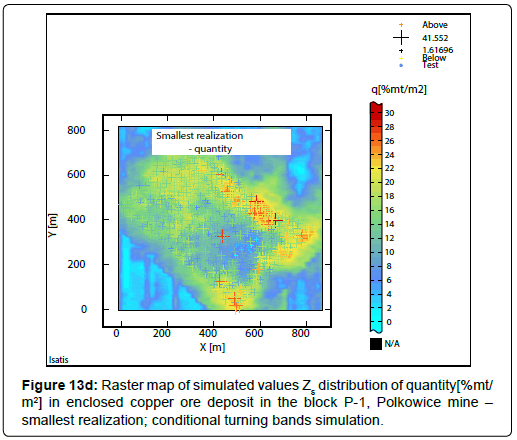
The results of conditional turning bands simulation: The obtained results of the using of conditional turning bands simulation are various. There can be mentioned - 100 raster maps of simulated values Zs (numbering from: 1 ÷ 100), the averaged picture (mean  ) is derived from 100 simulations (realizations Zs), the standard deviation of realizations σs from 100 simulations, the largest realization Zs from 100 simulations and the smallest realization Zs calculated from 100 simulations. 100 simulations was performed for each node of assumed elementary grid covering the P-1 block (count of grid nodes: N=3608). The results of the calculations connected with conditional turning bands simulation, concerning the quantity, were illustrated in raster statistical maps (Figures 13a-13d; Figures 14a-14c; Figures 15a-15d) and shown in Table 13.
) is derived from 100 simulations (realizations Zs), the standard deviation of realizations σs from 100 simulations, the largest realization Zs from 100 simulations and the smallest realization Zs calculated from 100 simulations. 100 simulations was performed for each node of assumed elementary grid covering the P-1 block (count of grid nodes: N=3608). The results of the calculations connected with conditional turning bands simulation, concerning the quantity, were illustrated in raster statistical maps (Figures 13a-13d; Figures 14a-14c; Figures 15a-15d) and shown in Table 13.
| Deposit parameter | Nugget effect C0 | Partial sill variance C’ | Total sill variance C | Range of influence a [m] | Basic model structures |
|---|---|---|---|---|---|
| Quantity [%mt/m2] | 0.3667 | 0.3152 0.5107 | 1.1927 | 154.60 361.60 | nugget effect spherical spherical |
Table 13: Global statistics of simulated values Zs of accumulation (quantity) [%mt/m2] in enclosed Cu ore deposit nin block P-1 of Polkowice mine; conditional turning bands simulation The values of basic statistics of accumulation (quantity) parameter is given in italics.
Mean value  calculated based on of 100 realizations Zs is a slightly higher than mean
calculated based on of 100 realizations Zs is a slightly higher than mean  of original values Z concerning quantity (Table 13). Coefficient V indicates small variation of realizations Zs.
of original values Z concerning quantity (Table 13). Coefficient V indicates small variation of realizations Zs.
Uncertainty
Assesssing the uncertainty in the estimates of quantity (accumulation)
A confidence interval for mean  calculated on the basis of simulated values Zs of quantity:
calculated on the basis of simulated values Zs of quantity:

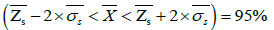
P(21.82 - 3.88< <21.82+3.88)=68%
<21.82+3.88)=68%
P(17.94<21.82<25.70)=68%
P(21.82 - 2 × 3.88< <21.82+2 × 3.88=95%
<21.82+2 × 3.88=95%
P(14.06<2<21.82<29.58=95%
A quality index may be calculated to classify each block into three categories [7].
Example of calculations of quality index
Confidence interval
Quantile 95%=23.81[%mt/m2],
Quantile 5%=15.47[%mt/m2],
Mean  of realizations Zs of quantity (accumulation)[%mt/m2] = 21.82 [%mt/m2].
of realizations Zs of quantity (accumulation)[%mt/m2] = 21.82 [%mt/m2].
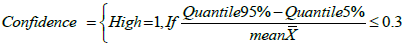
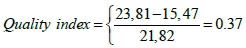
The obtained value of quality index=0.37 indicates a high confidence for the mining block P-1.
The results of the calculations connected with conditional turning bands simulation are presented in Table 13. It can be observed some regularities of variation. It can mention, among others, mean of realizations  and st. deviation of realizations σs, coefficients V of simulated values Zs for quantity (Table 13) are similar to these obtained, by using of ordinary kriging (Table 5). Coefficient V based on mean
and st. deviation of realizations σs, coefficients V of simulated values Zs for quantity (Table 13) are similar to these obtained, by using of ordinary kriging (Table 5). Coefficient V based on mean  of 100 realizations Zs reaches a small value. Coefficients V are much higher for standard deviation of realizations σs. The biggest value of the coefficient V calculated for the smallest realization Zs and much lower value coefficient V for the largest realization Zs were obtained.
of 100 realizations Zs reaches a small value. Coefficients V are much higher for standard deviation of realizations σs. The biggest value of the coefficient V calculated for the smallest realization Zs and much lower value coefficient V for the largest realization Zs were obtained.
The arithmetic mean  , based on the simulated values Zs, (realizations Zs, N=3608), evaluated in elementary blocks, is similar (Table 3) to the average
, based on the simulated values Zs, (realizations Zs, N=3608), evaluated in elementary blocks, is similar (Table 3) to the average  calculated using of original data Z, concerning quantity (N=788) (Table 13). Coefficient V of the simulated Zs values of indicates small changes of this parameter (I group of variations) within block P-1. Coefficient V determined on the basis of original values Z is higher (moderate variability). For two statistics - smallest realization Zs and standard deviation of realizations σs, the difference between the values of coefficient V of and coefficient V for original values Z (Table 1B, Table 10) is much bigger. The coefficient V for largest realization Zs reaches a relatively small value. This statistics is comparable with the coefficient V for original values Z (Table 13).
calculated using of original data Z, concerning quantity (N=788) (Table 13). Coefficient V of the simulated Zs values of indicates small changes of this parameter (I group of variations) within block P-1. Coefficient V determined on the basis of original values Z is higher (moderate variability). For two statistics - smallest realization Zs and standard deviation of realizations σs, the difference between the values of coefficient V of and coefficient V for original values Z (Table 1B, Table 10) is much bigger. The coefficient V for largest realization Zs reaches a relatively small value. This statistics is comparable with the coefficient V for original values Z (Table 13).
The coefficient V of standard deviation of realizations σs of qunatity has biggest value, indicating large variation (III group of variability).
Statistical simulation maps: Statistical raster maps of simulated values Zs, i. e. mean  of realizations Zs (Figure 13a), standard deviation of realizations σs (Figure 13b), smallest realization Zs, (Figure 13c) and largest realization Zs (Figure 13d) are presented in Figures 13a-13d.
of realizations Zs (Figure 13a), standard deviation of realizations σs (Figure 13b), smallest realization Zs, (Figure 13c) and largest realization Zs (Figure 13d) are presented in Figures 13a-13d.
Iso-cut-offs maps
In further studies the iso-cutoff maps above and below assumed thresholds were calculated. Iso-cutoff values maps with probabilities P values distribution for quantity: to be above assumed cutoff (Table 14) and to be below assumed cutoff (Table 15), have been determined with using of conditional turning bands simulation, assuming the same thresholds, as indicator cutoffs values, which earlier have been applied during bundled indicator kriging.
| Accumulation (Quantity) | Number of grid nodes N | Minimal value Xmin | Maximal value Xmax | Mean value  |
Standard deviation S | Variation coefficient V [%] |
|---|---|---|---|---|---|---|
| Ab. 20 [%mt/m2] | 3608 | 0.00 | 1.00 | 0.62 | 0.31 | 50 |
| Ab. 25 [%mt/m2] | 3608 | 0.00 | 1.00 | 0.27 | 0.27 | 101 |
| Ab. 30 [%mt/m2] | 3608 | 0.12 | 1.00 | 0.91 | 0.13 | 14 |
| Ab. 35 [%mt/m2] | 3608 | 0.00 | 0.28 | 0.02 | 0.05 | 198 |
Table 14: Global statistics of probability P values (above assumed thresholds) of accumulation (quantity) [%mt/m2] in enclosed Cu ore deposit in block P-1 of Polkowice mine; conditional turning bands simulation.
| Accumulation (Quantity) | Number of grid nodes N | Minimal value Xmin | Maximal value Xmax | Mean value  |
Standard deviation S | Variation coefficient V [%] |
|---|---|---|---|---|---|---|
| Bel. 20 [%mt/m2] | 3608 | 0.00 | 1.00 | 0.38 | 0.31 | 81 |
| Bel. 25 [%mt/m2] | 3608 | 0.00 | 1.00 | 0.73 | 0.27 | 37 |
| Bel. 30 [%mt/m2] | 3608 | 0.12 | 1.00 | 0.91 | 0.13 | 14 |
| Bel. 35 [%mt/m2] | 3608 | 0.72 | 1.00 | 0.98 | 0.05 | 5 |
Table 15: Global statistics of probability P values (below assumed thresholds) of accumulation (quantity) [%mt/m2] in enclosed Cu ore deposit in block P-1 of Polkowice mine; conditional turning bands simulation.
The largest probability P average value (0.91) and the smallest value of the variation coefficient V (14%) were obtained with the assuming of the threshold above 30 [% mt/m2] (Table 14).
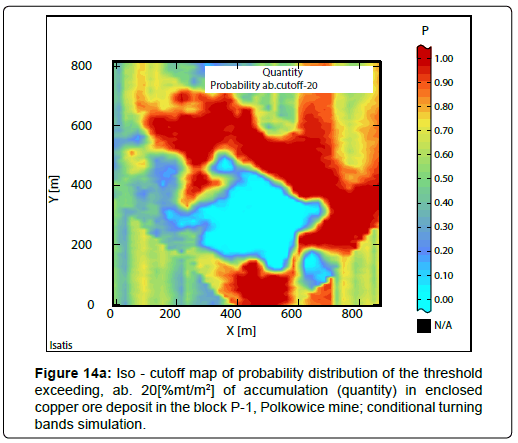
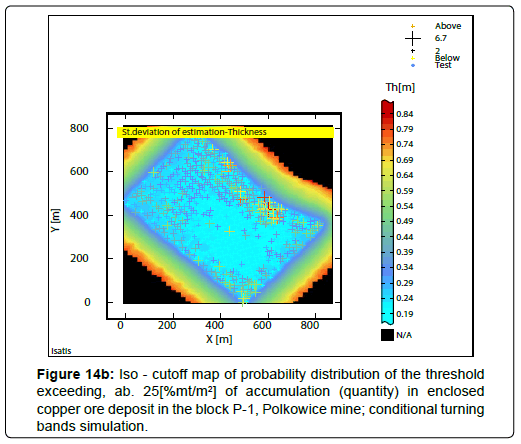
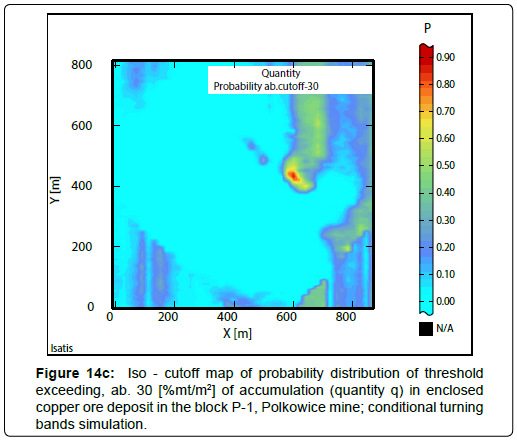
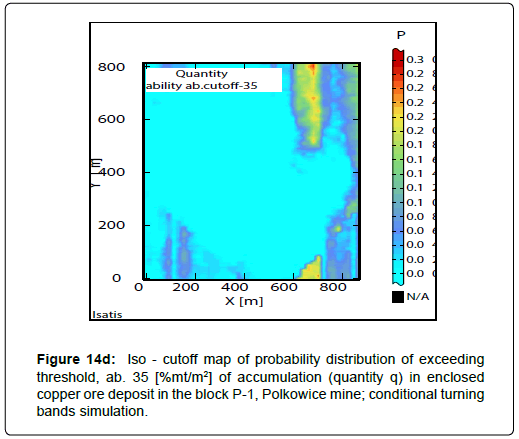
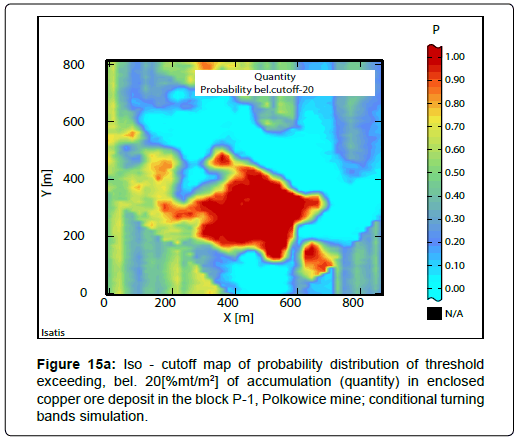
Iso-cut-offs maps determined from the results of conditional turning bands simulation have been shown in the Figure 14a-14d and Figure 15a-15d. Raster iso-cut-offs maps, calculated to be above assumed cutoffs for the quantity are presented in Figure 14a,14b.
For the threshold>20[%mt/m2], a large sub-area showing the largest P values (0.9 to 1.0), within the P-1 block, was obtained (Figure 14a). With increasing of the threshold value to>25[%mt/m2], the sub-area with the largest P values significantly decreases (Figure 14b). For larger value of threshold>30[%mt/m2], only very small subblocks with highest probability P values were separated (Figure 14c). For the threshold>35[%mt/m2], P values are very low, contained in the limits 0.20-0.30 (Figure 14d).
Uncertainty: Probability intervals for mean  calculated on the basis of simulated values Zs of quantity (ab. assumed threshold):
calculated on the basis of simulated values Zs of quantity (ab. assumed threshold):
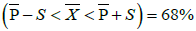
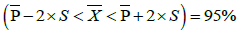
Above cutoff – 20[%mt/m2]
P(0.62 – 0.31< <0.62+0.31)=68%
<0.62+0.31)=68%
P(0.31<0.62<0.93)=68%
P(0.62 - 2 × 0.31< <0.62+2 × 0.31)=95%
<0.62+2 × 0.31)=95%
P(0.00<0.62<1.24)=95%
Above cutoff – 25[%mt/m2]
P(0.27 – 0.27< <0.27+0.27)=68%
<0.27+0.27)=68%
P(0.00<0.27<0.54)=68%
P(0.27 - 2 × 0.27< <0.27+2 × 0.27)=95%
<0.27+2 × 0.27)=95%
P(-0.27<0.27<0.81)=95%
Above cutoff – 30[%mt/m2]
P(0.09 – 0.13< <0.09+0.13)=68%
<0.09+0.13)=68%
P(-0.04<0.09<0.22)=68%
P(0.09 - 2 × 0.13< <0.09+2 × 0.13)=95%
<0.09+2 × 0.13)=95%
P(-0.17<0.09<0.35)=95%
Above cutoff – 35[%mt/m2]
P(0.02 – 0.05< <0.02+0.05)=68%
<0.02+0.05)=68%
P(-0.03<0.02<0.07)=68%
P(0.02 - 2 × 0.05< <0.02+2 × 0.05)=95%
<0.02+2 × 0.05)=95%
P(-0.08<0.02<0.12)=95%
The biggest confidence level can be obtained for the cutoff above 20[%mt/m2].
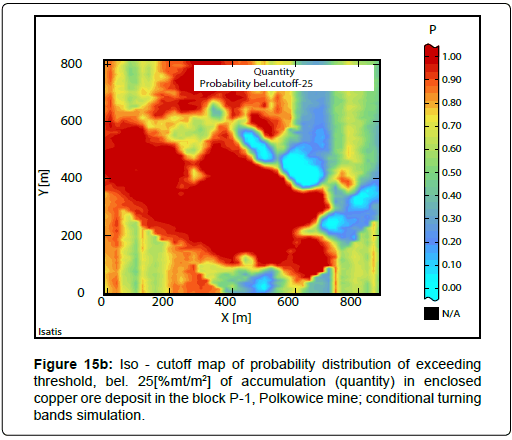
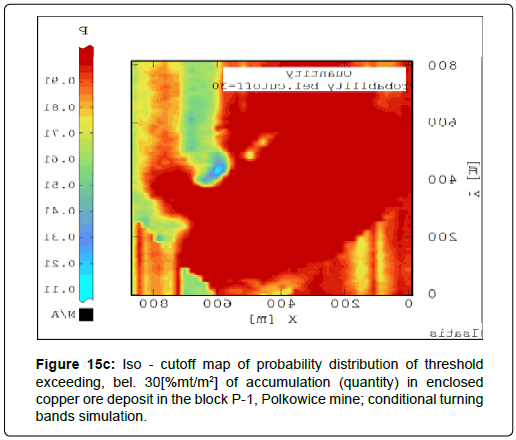
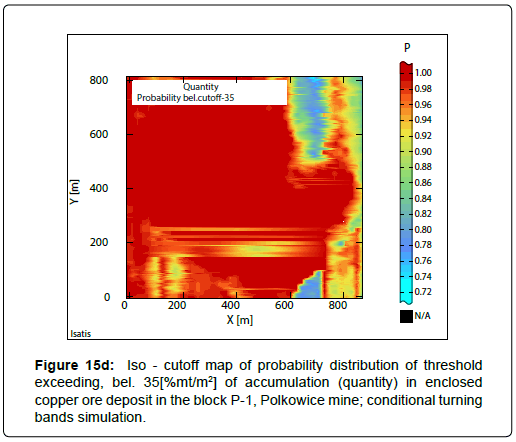
Raster iso-cut-offs maps, calculated to be below assumed cutoffs for the quantity are illustrated in Figures 15a-15b.
The largest probability P average values (0.91 ÷ 0.98) and the smallest values of the variation coefficient V (5 ÷ 14%) were obtained with the assuming of the thresholds, below 30[%mt/m2] and 35[%mt/ m2] (Table 15).
Iso-cutoff maps calculated, assuming thresholds, bel. 20[% mt/ m2], 25[% mt/m2], 30[% mt/m2], 35[% mt/m2] reflect earlier viewed images on iso-cutoff maps calculated ab. these values (Figures 15a-15d). This applies to the shapes of determined subareas and the calculated ranges of P values.
Uncertainty: Probability intervals for mean  calculated for simulated values Zs of quantity (bel. assumed cutoff):
calculated for simulated values Zs of quantity (bel. assumed cutoff):
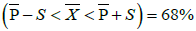
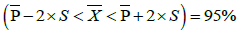
Below cutoff- 20[%mt/m2]
P(0.38 – 0.31< <0.38+0.31)=68%
<0.38+0.31)=68%
P(0.07<0.38<0.69)=68%
P(0.38 - 2 × 0.31< <0.38+2 × 0.31)=95%
<0.38+2 × 0.31)=95%
P(-0.24<0.38<1.00)=95%
Below cutoff- 25[%mt/m2]
P(0.73 – 0.27< <0.73+0.27)=68%
<0.73+0.27)=68%
P(0.46<0.73<1.00)=68%
P(0.73 - 2 × 0.27< <0.73+2 × 0.27)=95%
<0.73+2 × 0.27)=95%
P(0.19<0.73<2.27)=95%
Below cutoff – 30[%mt/m2]
P(0.91 – 0.13< <0.91+0.13)=68%
<0.91+0.13)=68%
P(0.78<0.91<1.04)=68%
P(0.91 - 2 × 0.13< <0.91+2 × 0.13)=95%
<0.91+2 × 0.13)=95%
P(0.65<0.91<1.17)=95%
Below cutoff – 35[%mt/m2]
P(0.98 – 0.05< <0.98+0.05)=68%
<0.98+0.05)=68%
P(0.93<0.98<1.03)=68%
P(0.98 - 2 × 0.05< <0.98+2 × 0.05)=95%
<0.98+2 × 0.05)=95%
P(0.88<0.98<1.08)=95%
The biggest confidence levels can be noticed for two cutoffs below 30[%mt/m2] and 35[%mt/m2].
The efficiency of estimation and simulation
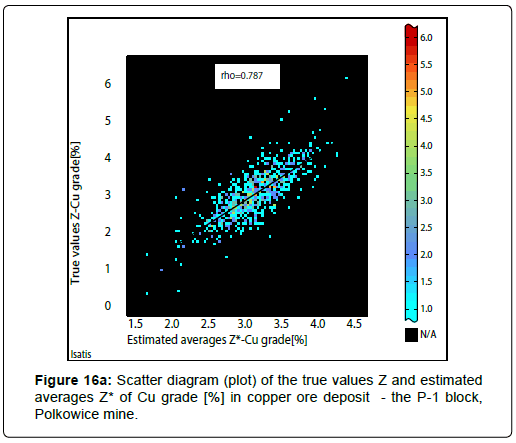
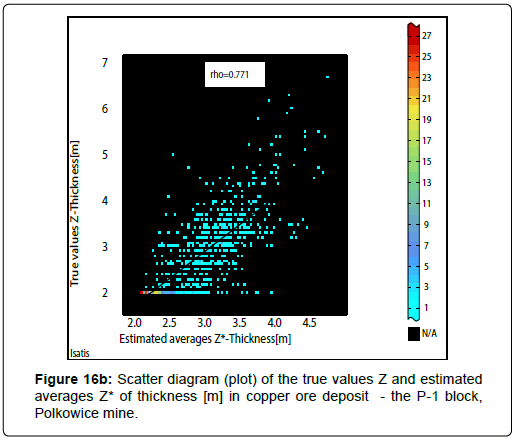
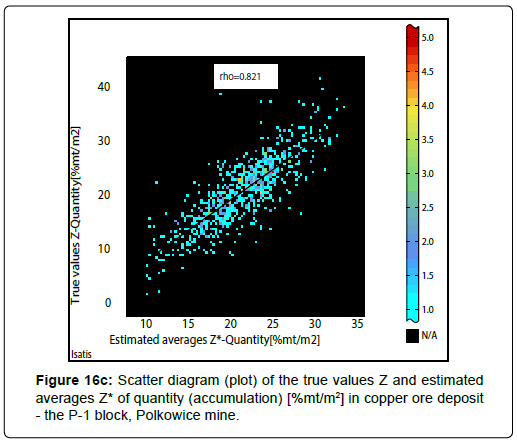
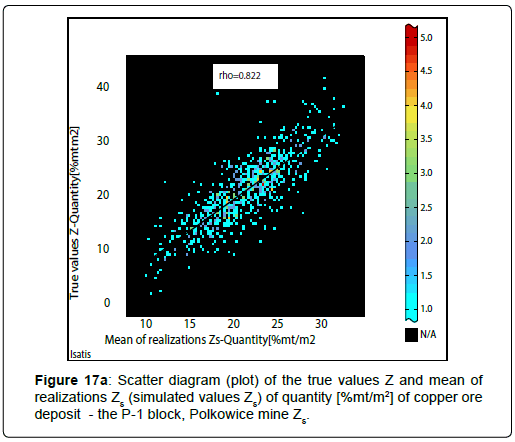
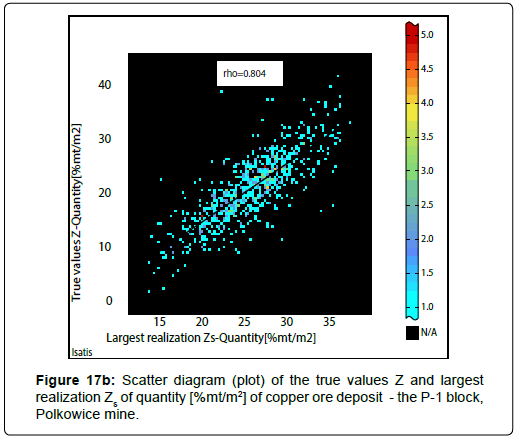
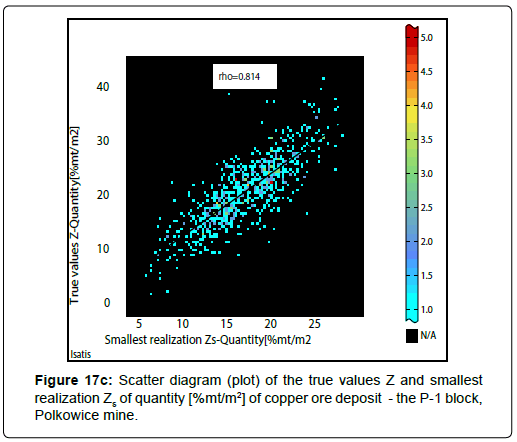
The quality of the conducted estimation and the simulation is very good, which is proved by the scatter diagrams, i.e. plots of the true Z values and estimated averages Z * (kriging estimates) and scattering plots for the original values Z and simulated values Zs (realizations Zs) of the deposit parameters. High values of the correlation coefficient r were obtained, regardless of the method used (ordinary block kriging, Figures 16a to16c; conditional turning bands simulation, Figures 17a to 17c).
If ordinary block kriging has been used to estimate of averages Z* of Cu grade and thickness, the values of coefficients r have been a little lower (r: 0.771-0.787) (Figures 16a, 16b). In case if conditional turning bands simulation was applied to simulate the quantity, the values of correlation coefficients r have been reached a slightly higher values (r: 0.804- 0.822) (Figure 17a to 17c). It concerns also the results of estimation of quantity performed, using ordinary block kriging (Figure 16c).
It should be emphasized that this is a very high correlation between the studied parameters (according to the classification of J. Guilford).
A comparison of the results of bundled indicator kriging and conditional turning bands simulation: In general, the subareas of highest and lowest probabilities P values determined in the raster maps are similar, close, especially for lower cutoffs values, are convergent, occur in similar places. If we use bundled indicator kriging, obtained pictures are more smoothed, while the images obtained from conditional turning bands simulation are more detailed, independently on applied cutoff-value or threshold. This last technique gives better mapping of details, fluctuation of variation of ledge parameters than it can be related to the results of indicator kriging. In particular, it should be noticed to the images obtained by assuming of lower thresholds of quantity, 20 [%mt/m2] and 25[%mt/ m2] (Figure 14a-14b; 15a-15b).
Indicator maps, which were calculated for the lowest cutoff values - 2.2 Cu[%] (Figure 9a), 2.5 m (Figure 10a), 20[%mt/m2] (Figure 11a) and obtained by means of conditional turning bands simulation for threshold - 20[%mt/m2] (Figure 14a) prove, that the assuming of these thresholds was completely justified. High values P prevail within the whole area of the P-1 block (Figures 9a,11a,14a), what is visible, in particular, for Cu grade.
In probability maps, calculated using the indicator kriging, one can see that in the vast majority of the P-1 mining area Cu grade exceeds 2.2% Cu. In the case of a cut-off value of thickness - 2.5 m, it is not so extensive sub-area, as for Cu grade, however, nevertheless large area is observed. A similar remark can apply to the quantity above cutoff - 20[%mt/m2], i.e. to probability maps calculated, using bundled indicator kriging, as well as conditional turning bands simulation. It can therefore be assumed that if a cut-off value of 2 m has been assumed for the thickness, then the sub-area surface showing large probability values P would be much larger for both parameters (thickness, quantity).
P-probability images obtained using conditional turning bands simulation calculated above assumed accumulation thresholds, complement and confirm maps drawn out on the assumption of values of this parameter, below tested thresholds (Figures 14a-14d; 15a-15d).
Summing Up of the Results of Spatial Analyses
Used geostatistical methods, i.e. ordinary kriging, bundled indicator kriging and conditional turning bands simulation are effective tools to characterize, estimate and manage mineral resources, i.e. Zechstein sedimentary Cu ore deposits occurring in the region Lubin-Sieroszowice (SW Poland).
The results of all performed geostatistical studies show, that a good quality of the obtained evaluations, i.e. correspondence of estimated averages Z* and simulated values Zs with original (true) data Z, coming from sampling of copper deposit in the post- exploitation block P-1, is observed.
Among the analyzed deposit parameters, the deposit thickness is the most variable parameter.
The thickness and quantity of the deposit show a stronger variability than the Cu grade, which is indicated by the results of evaluation of basic statistics of the original Z values, the results of modelling of semivariograms and estimating of averages Z* of the deposit parameters.
The values of standard deviation of estimation σk, coefficients V of the deposit parameters are higher, as for Cu grade. Some difficulties with the choice of proper theoretical models of empirical variograms, caused by an occurrence of significant changes of thickness within certain parts of the P-1 block, appear. Obviously, this affects also the results of quantity calculations.
Discussion and Conclusion
The results of isotropic semivariograms modelling show smallscale and large-scale variation, i.e. a low frequency and a high frequency for the studied deposit parameters. Shortest ranges of influence a characterize isotropic semivariogram of Cu grade. Similar remarks can be related to indicator semivariograms of this parameter. The results of modelling of indicator semivariograms confirm a nested character of variation of the deposit parameters.
The proposed techniques bundled indicator kriging and conditional turning bands simulation are useful tools for the determining of an anomalous zones, in the area of an occurrence of the deposit.
Conditional turning bands simulation is more labor-intensive in practical applications than bundled indicator kriging. However, this technique has extensive computing and wide, richest visualization capabilities and permits for the conducting further more detailed spatial analyses.
The use of a conditional turning bands simulation allowed for obtaining of simulation models of the ledge parameters of the copper ore deposit “Polkowice”.
In the example presented in the article, 100 raster maps of simulated values Zs, the images averaged based on simulated values Zs, - mean  standard deviation of realizations σs, as well as maps of largest simulated value Zs and smallest simulated value Zs, moreover iso-cut-offs maps for the assumed (above and below) threshold values, were calculated. These obtained results can constitute the basis for further, more detailed, spatial analyses.
standard deviation of realizations σs, as well as maps of largest simulated value Zs and smallest simulated value Zs, moreover iso-cut-offs maps for the assumed (above and below) threshold values, were calculated. These obtained results can constitute the basis for further, more detailed, spatial analyses.
Sub-areas with rich, an anomalous Cu compounds concentrations, corresponding to the occurrence of richly mineralized copperbearing shales within the P-1 block, are marked in raster maps of distributions of estimated averages Z* and simulated values Zs. Small subareas with large thicknesses of the whole deposit series, associated, mainly, with considerable thicknesses of mineralized carbonate rocks and of mineralized sandstones occur in raster maps of averages Z* of thickness.
References
- Armstrong M (1998) Basic linear geostatistics. Springer Science & Business Media, USA, pp: 153.
- Armstrong M, Matheron G (1987) Geostatistical case studies. Springer Science & Business Media, USA
- Geovariances (1998) On the use of non-linear geostatistical techniques for recoverable reserves estimation: A practical case study, Geovariances, Avon-Fontainebleau, France, pp: 11.
- Geovariances (2015) Geostatistics for Mining Engineers and Geologists, Avon-Fontainebleau, France.
- Geovariances (2014) Uncertainty of mineral resource estimates from confidence intervals to resource classification. Avon-Fontainebleau, France, pp: 8.
- Geovariances (2015) Which block size for mineral resource estimation. White Paper, pp: 8.
- Geovariances (2015) Use of simulations for mining applications. White Paper, pp: 8.
- Isatis (2015) Geostatistics software for improved mining resource estimation geovariances, Avon-Fontainebleau, France.
- Isatis (2015) Software user’s guide Ecole des Mines de Paris, Centre de Geostatistique, Fontainebleau, Geovariances, Avon Cedex, France.
- Isaaks EH, Srivastava RM (1989) An introduction to applied geostatistics. Oxford University Press, USA.
- Isatis (2017) The latest edition of the Isatis manual, Geovariances, France.
- Matheron G (1987) Geostatistical case-studies (Quantitative) geology and geostatistics. Springer, USA.
- Mucha J (1994) Metody geostatystyczne w dokumentowaniu złóż (Geostatistical methods in deposit documentation. AGH Akademia Górniczo-Hutnicza, pp:155.
- Mucha J, Nieć M (1996) Structure of variability of deposit parameters, Monograph KGHM Polska Miedź SA Lubin, pp: 195-200.
- Mucha J, Wasilewska M (2009) Three-dimensional modeling of deposit parameters values ​​using the 3D ordinary kriging method. Geologia, AGH, im. Stanisława Staszica w Krakowie 35: 167- 274.
- Namysłowska-Wilczyńska B (1993) Variability of the copper deposit of the Przedsudec monocline. Geology Sudetica 12: 207.
- Namysłowska-Wilczyńska B (2006) Geostatystyka-Teoria i Zastosowania. Oficyna Wydawnicza Politechniki Wrocławskiej, Wrocław, pp: 356.
- Namysłowska-Wilczyńska B (2012) Geostatistical methods used to estimate Sieroszowice copper ore deposit parameters. J Geo Sci 40: 329-361.
- Namysłowska-Wilczyńska B (2013) Uncertainty estimation through geostatistical simulations. 3rd International Seminar on Geology for the Mining Industry, Santiago, Chile.
- Namysłowska-Wilczyńska B (2014) Studium modelowania i szacowania porfirowego złoża miedzi Rio Blanco w Peru”. 3D modelling and estimating of Rio Blanco porphyritic copper deposit in Peru. WTN Wrocławskie Towarzystwo Naukowe, Wrocław, Poland.
- Namysłowska-Wilczyńska B (2015) Application of turning bands technique to simulate values of copper ore deposit parameters in Rudna mine (Lubin - Sieroszowice region in SW part of Poland). Georisk: Assessment and Management of Risk for Management and Engineered Systems and Geohazards 9: 224-241.
- Namysłowska-Wilczyńska B (2018) Application of geostatistical techniques for the determining of anomalous zones of copper ore deposit. The 19th Annual Conference of the International Association for Mathematical Geosciences.
- Namysłowska-Wilczyńska B (2018) Filtration of components of Sieroszowice Mine copper ore deposit variogram models by means of estimation ordinary kriging technique. Geoinform Geostat: An Overview 6: 1-19.
- Wackernagel H (1998) Multivariate Geostatistics: An Introduction with Applications. Springer, Berlin. pp: 256.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi