Research Article, J Tourism Res Hospitality Vol: 6 Issue: 1
Impacts of Cyclic Patterns of Climate on Fluctuations in Tourism Demand: Evidence from Aruba
| Marck Oduber1* and Jorge Ridderstaat2 |
| 1International Centre for Integrated assessment& Sustainable development (ICIS) Maastricht University PO Box 616, 6200 MD Maastricht, The Netherlands a/o Director Meteorological Department, Aruba |
| 2Central Bank of Aruba J.E. Irausquin Boulevard 8, Aruba |
| Corresponding author : Marck Oduber International Centre for Integrated assessment& Sustainable development (ICIS) Maastricht University PO Box 616, 6200 MD Maastricht, The Netherlands a/o Director Meteorological Department Aruba Oranjestad, Aruba E-mail: marck.oduber@meteo.aw |
| Received: July 14, 2016 Accepted: December 31, 2016 Published: January 03, 2017 |
| Citation: Oduber M, Ridderstaat J (2017) Impacts of Cyclic Patterns of Climate on Fluctuations in Tourism Demand: Evidence from Aruba. J Tourism Res Hospitality 6:1. doi: 10.4172/2324-8807.1000159 |
Abstract
Impacts of Cyclic Patterns of Climate on Fluctuations in Tourism Demand: Evidence from Aruba
This study estimates the influence of long cyclical climate patterns of pull and push climate elements (rainfall, temperature, wind) on cyclical fluctuations in tourism demand from the United States, the Netherlands and Venezuela on a small island state. Two important atmospheric variabilities, the El Niño Southern Oscillation (ENSO) and the North Atlantic Oscillation (NAO), were also included. Wavelet analysis was used because meteorological and economical time-series are typically noisy, complex and strongly non-stationary. Results show that both pull and push cyclical climate factors had an influence on tourism demand from the USA, the Netherlands and Venezuela. Furthermore, ENSO and NAO had also an influence on tourism demand from the USA and the Netherlands. The finding of a statistical relationship between atmospheric variabilities and tourism suggests that that they should be taken into account when developing tourism demand models, in order to create simpler econometric models.
Keywords: Cyclic pattern; Tourism demand; Wavelet analysis; Aruba; El Niño; North Atlantic oscillation
Keywords |
|
| Cyclic pattern; Tourism demand; Wavelet analysis; Aruba; El Niño; North Atlantic oscillation | |
Introduction |
|
| The purpose of the study is to investigate how long cyclical patterns of climate influence tourism demand in small island destinations. Climate and weather play detrimental roles in the selection process of a tourist destination. Studying climate cycles relationship to tourism cycle may provide a better understanding in the complicated process of tourist visit fluctuations on a destination. Cycles are generally defined as systematic variations that have the property of repetition [1]. In this context, for example, a business cycle can be defined as a fluctuation of economic activity that shows non seasonal pattern. Some business cycles are Kitchin cycle, Juglar cycle, Kuznets cycle, and Kondratieff cycle [1]. Kitchen cycles are short period cycles of 3 to 5 years, Juglar cycles are 7 to 11 years, Kuznets cycles are 15 to 25 years, whereas Kondratieff are the longer cycles of 45 to 60 years. Tourism demand cycles could, in an economical sense, be considered as results of variations of the overall economic activity. Therefore, according to Kožić [1], tourism demand cycles can be explained by influence of the overall economic activity. Studies done by Guizzardi & Mazzocchi [2], also hint that tourism cycles can be heavily influenced by the overall business cycle. Where Gouveia and Rodrigues [3] found the presence of a repetitive time lag among turning points of business and tourism demand growth cycles. Certain authors have also tried to relate money supply cycles in destination country with tourism demand cycles in arrival country [4]. These authors showed that money supply cycles can influence the cyclical movements of tourism demand and that the impacts are asymmetric depending on the time of development of the cycles [4]. | |
| Over the past century, tourism has become the world’s biggest business, exceeding defence, manufacturing, oil and agriculture industries [5,6]. Tourism is one of the fastest growing segments and this is a unique feature since World War II [7,8,9,10]. To stay upto- date to the rapidly growing tourism phenomenon, destinations must have proper projections of tourism demand for planning and managerial decisions. Therefore an adequate insight into the factors that influence tourism is needed. These factors should, also, include non-economic factors. Most studies on the determinants of tourism demand have been focused around economic aspects (e.g. income and price), while remaining mostly silent on the potential impact of climate on the selection of destinations [11]. Climate is defined as the total of all statistical weather information that aids to describe the variation of weather at a given place for a specified interval of time [12]. Climate can be seen as the average weather for a particular location that influences a wide array of environmental resources, which are critical attractions for tourism, for example, snow conditions, wildlife productivity and biodiversity, and water levels and their quality [13]. On the other hand, weather is the state of the atmosphere, mainly with respect to its effect upon life and human activities at a particular time, as defined by the various weather elements [12]. | |
| Since the beginning of reliable instrumental records it has been possible to make approximations of the degree to which various aspects of economic activity have been influenced by anomalous weather events [14]. Severe winters of 1947, 1963, and 1979 all have caused major economic disruptions across Europe [14]. Cyclic behaviour in climate such as El Niño’s of 1982/83 and 1997/98 had major global impacts. From droughts in Australia to many part of the sub-Saharan Africa, Brazil and Central America [14]. Except for economic impacts, climate can have an influence on tourism too. Climate can attract visitors who expect pleasant weather conditions at a destination [15,16]. While on the other hand climate can influence a traveler’s decision to leave or stay in his/her own country [17]. Henceforth, climate can act as both a pull and a push factor that influences the motivations of tourists to go on a holiday and how they choose their destination of preference [18,19]. These push and pull factors can, therefore induce oscillations in tourism demand. | |
| Reduction in demand can induce conditions such as of overcapacity, non-utilization of infrastructure, decrease in the workforce, and absence of investments during low seasons can induce reduced profitability and productivity [20,21]. In contrast, peak seasons of tourism can be characterized by overuse of public utilities (e.g. water supply, waste management, and road use), causing discontent for inhabitants and visitors alike, while the environment can suffer permanent damage because of tourism burdens [22]. | |
| Studies on climate and tourism such as Ridderstaatet al. [11,23] have focused on the seasonal patterns, intra-annual, inter-annual scales of climate and not cyclic patterns. Others have used climatological data in order to investigate general tourism activities for a region, but not long cyclic events and tourism itself [24]. A study done by Moreno et al. [25], has reviewed the relationship between weather conditions and beach recreation by studying tourists behavior. In their study they used daily weather condtions and webcam data to get an idea on the movement of tourist in a certain area. Here again the focus was on short-term climate patterns that influence the movement of tourist, not on cyclic events that have an influence on tourism demand. Furthermore Alvarez-Diaz et al. [26] indicate that in general little systematic research has been done on climate as a significant determinant of of tourism demand. Alvarez-Diaz et al. [26] indicate that only recently, a number of studies have analyzed the impact of climate and weather variables on tourism. Álvarez-Díaz, et al. [26], themselves have studied as a novum, the North Atlantic Oscillation (NAO) and variability on tourism arrivals from the United Kingdom and Germany to Spain. | |
| To our knowlegde the study by To our knowlegde the study by Ridderstaat et al. [11], was the only one that has studied howseasonal push and pull climate patterns, can influence seasonalmovements of tourism demand on a small island. In view of the lack of studies which investigate how cyclical climate patterns influences cyclical patterns of tourism demand especially in small island destinations, there is a case for better understanding of the drivers of tourism demand in small island economies. Croes [27] shows that, many small islands use tourism development as a growth strategy for greater economic and development performance. The positive contribution from specializing in tourism has aided to more than balance the negative impact of being a small island economy, and tourism has been a significant contributor to lower output volatility in many countries [28]. | |
| This study investigates whether cyclic patterns of pull and push climate elements (including rainfall, wind, and temperature) affect the cyclical deviations of tourism demand for a small destination like Aruba. Individual case studies can contribute to scientific generalizations through the replication outcome, where the mode of generalization is analytical generalization [29]. The aim then is to develop and generalize theories, and not to enumerate frequencies (statistical generalizations). According to Eisenhardt and Graebner [30], building theory from case studies is a research strategy, which requires at least one case to create theoretical, constructs, propositions and/or midrange theory from case-based empirical evidence. | |
| The methodology involves a wavelet analysis of tourism demand and climate factors. Wavelet analysis comprises of transformations of a data series through a wavelet, and a localized wave [31]. The data is rearranged into frequency domain, where periodic behaviour is more easily seen [31]. Wavelet analysis is well suited for studies of multiscale, non-stationary processes that occur over finite spatial and temporal domains [32]. In the case of tourism demand and climate factors it can differentiate multi-annual patterns of variation from a seasonal component. Wavelet analysis is also coherence in which the frequency components of different time-series can be compared directly [31]. Therefore wavelet analysis gives two major benefits: first it allows separtion of influences by time-scale and secondly it gives a domain in which to measure nonstationary association [31]. | |
| The present study allows for some key contributions to the tourism literature. Firstly it adds to the further understanding of the specific role of patterns of cyclic climatic variables on the cyclic pattern of tourism demand. Secondly this investigation also simultaneously analyses the impact of both pull and push climate factors on cyclical tourism demand movements on a small island, which, as far as we can perceive, is not common when it comes to time-series based studies on this relationship. The rest of this paper is organized as follows. Section 2 discusses material and methods. In section 3, results and discussion are presented, whereas section 4 concludes and offers policy implications and lines for future research. | |
Materials and Methods |
|
| Case study Aruba | |
| Aruba is a small island state positioned about 32 km from the Northern coast of Venezuela, and has only an area of about 180 km2. Aruba is considered as an autonomous country within the Kingdom of the Netherlands, which consists of The Netherlands, Aruba, Curacao and Sint Maarten. Aruba’s capital is Oranjestad and Aruba’s total population is around 110 thousand [33]. Aruba is popularly referenced also as part of the ABC islands, which consists of Aruba, Curacao and Bonaire. | |
| Unlike many other islands in the Caribbean, Aruba has a very dry and windy climate. Aruba’s climate is classified as a tropical steppe, semiarid hot climate with the wind coming for more than 95% of the time from the northeast and the southeast direction over Aruba, with an average speed of 7.3 m s-1 at 10-meter distance (1981-2010) [34]. On average Aruba’s temperature is 27.9º Celsius, but the temperature can fluctuate between 19.0º Celsius to 36.5º Celsius. The average rainfall for Aruba for the period 1981-2010 is 471.1 mm [34]. Even though Aruba has a dry and windy climate, the island still has still managed to become a popular tourist destination. | |
| Aruba has a bit more than half a century of experience with the tourism industry. Its first 100-room, hotel was built in 1959 and modeled after similar ones in Florida and Puerto Rico [11]. Given the dominant role of the Lago Oil & Transport Company, Ltd, tourism played only a small part in the overall economic development of the island in the beginning. This situation changed in 1985, when the oil refinery closed its doors, and causing a considerable shock to the Aruban economy [35]. This precarious situation forced the Aruban government to search for new sources of economic activity. The most tangible way was to expand the tourism industry. The amount of hotel rooms more than tripled, from 1986 to 2011, where the majority of visitors came by airplane [11]. The United States tourist, accounted on average for roughly 63.5% of all stay-over visitors between 1981- 2011, this makes the United States the biggest market for Aruba. The Venezuelan market is the second largest for the island, accounting on average for about 13% of all stay-over visitors to the island [11]. | |
| Data collection | |
| The basis for this study is the conceptual scheme depicted in Figure 1, where relationships will be investigated between, on one hand push climate patterns, on the other hand pull climate patterns, and tourism demand, in the middle. Matzarakis [36], shows that the most relevant meteorological parameters when it comes to tourism include air temperature, air humidity, wind speed, wind direction, cloud coverage, sunshine duration, or radiation fluxes, rain and precipitation, snow coverage, and water temperature. For the purpose of this study, we use three weather fundamentals (rainfall, temperature, and wind speed) as pull factors (i.e. the weather conditions in arrival country that attract visitors), and three weather elements (rainfall, temperature, and wind speed) as push factors (i.e. weather conditions departure country that cause residents to travel to destinations like Aruba) (Figure 1). | |
| Figure 1: Conceptual framework of the relation between the cyclical patterns of (pull/push) climate data and tourism demand of Aruba’s tourism. | |
| The raw variables used in this investigation are shown in Table 1. Climate data for Aruba are from the Meteorological Department of Aruba. The related data for the USA are from the North-Eastern part of that country, given that most US visitors to Aruba are from that region. The climate data for this country come from several sources, including the Global Precipitation Climatology Centre and the European Centre for Medium-Range Weather Forecasts. Climate data for the Netherlands and Venezuela (Caracas) are from the same sources as those of the USA. | |
| Table 1: Raw variables used in the analysis. | |
| Tourism demand is approximated by the number of visitors from the Netherlands, the North-Eastern part of the USA, and Venezuela. The data were collected from the Central Bank of Aruba | |
| Wavelet analysis | |
| Meteorological and economic data can be substantially nonstationary [32,37]. Therefore the authors performed wavelet decomposition, which is a statistical analysis on time-series allowing for efficient dealing with non-stationary data. In order to perform wavelet analysis, one has to choose a basic function for the transformation. For this study we used the Morlet wavelet, which is a complex sine wave localized by a Gaussian distribution according to the following formula | |
| Where Ƞ is a scaled time variable, describing the relative frequency ω0 of the sine wave [31]. We used a non-dimensional frequency ω0=6, which is used in ecological, geophysical and economic studies [38,39,40]. The continuous wavelet transform consists of the convolution of the series xn and the wavelet ψ0 at time t and scale s, where xn consists of a series of observations x0, ...,xN-1 spaced equally in time by δt [31]. As described in Johansson, Cummings and Glass, [31], this is defined as | |
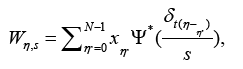 |
|
| where the parameter ψ* is the complex conjugate of the wavelet that is normalized by a factor of (δt/s)1/2 to ensure unit energy, and allowing comparability between scales and analyses. In order to adjust the time-frame to a more meaningful scale, the parameter δt is included. Wavelet transformations are complex and describe time and frequency-specific power and phase. The strength of the waveletlike behavior at every point is indicated by the power |Wn,s|2, and is indicated in the power spectrum of each transformation. The angular position of each point in its cyclical trajectory is given by the phase (θ). It varies from a trough at π radians to a peak at 0 or 2π radians. The phase (θ) is calculated as the inverse tangent of the imaginary component of the transform divided by the real component [31]: | |
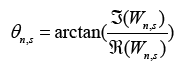 |
|
| The wavelet can extend itself both forward and backward in time. Therefore the beginning and end of a time-series are effectively joined in a loop so that there is prior and post information at any point [31]. To avoid this, the authors pad the time-series with zeros to the next power of 2 of their length, in line with Torrence and Compo [41]. Since the zeros still have an influence on the transformation at the extremities, the area of the transform is masked where edge effects are significant [31]. Given that the Morlet wavelet is a complex wavelet, it allows to quantification of the phase and therefore it can calculate time-lags between different time-series. Coherence based on wavelets allows one to do similar analysis as cross-correlation even for possible nonstationary signals [39]. In this study wavelet coherences were calculated to examine the association between different time-series, both in time and frequency. Coherence spectra allows one to investigate whether different periodic modes of two time-series tend to oscillate concurrently, and, if they do, one can identify the periodicity around which this relationship takes place [39]. For this study we calculated the squared coherency (R2), | |
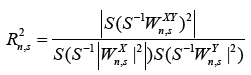 |
|
| Where S-1 will normalize the energy, Wx is one wavelet transform variable, Wy is the other variable, Wxy is the cross-wavelet spectrum (WxWy) and S(W) is the sequential smoothing function Sscale (Stime) following Johansson et al. [31]. The scale specific convolution of W with a normalized Gaussian filter is defined as Stime. Sscale is the time specific convolution of the result with a normalized boxcar filter [31]. As indicated by Johansson et al. [31] the denominator of the power spectra is smoothed prior to finding the modulus and squaring. Significance levels were calculated using a Chi-square test assuming that the wavelet coefficients are normally distributed, in line with Torrence and Compo [41]. | |
| The phase of the coherency can also be calculated. This will give one time and frequency specific differences in phase between the twotime series [31]: | |
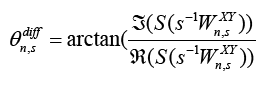 |
|
| For a more in depth description of the theory for wavelet analysis, please refer to Cazelles et al. [42], and Torrence and Compo [41]. | |
| Before wavelet decomposition, the applied time-series were altered by a Box-Cox power transformation, in order to make the distribution values more symmetrical and induce a variance-stabilizing effect, following Wilks [43]. As shown by Osborne [44], Box-Cox power transformations were superior to traditional transformations, such as square root, log, and inverse. Hinkley’s dλ statistic was used to find the best transformation parameter, in line with Wilks [43]. Imputations for missing values were done in the Dutch tourism data through a kalman filter, based on state space methods, following Durbin & Koopman [45]. Loess smoother was also applied to the data to remove any trend similar to Cleveland [46], Cleveland et al. [47]. The idea of a locally weighted regression, or loess, procedure is fitting a regression surface data through multivariate smoothing. The dependent variable is smoothed as a function of the independent variables in a moving manner, analogous to how a moving average is calculated for a timeseries [48]. All analyses were conducted in Microsoft Excel (2010) and R [49]. Wavelet analyses were performed using the “WaveletComp” R package [50]. | |
Results and Discussion |
|
| Figure 2a, 2b, 2c shows the wavelet power spectrum for tourism demand from USATOUR, VENTOUR, and HOLTOUR. High power will indicate frequency and time specific periodicity [31]. Since we are mainly interested in cyclic variations, we looked only between 24 to 256 months (1 to 21 years). Since we were interested in non-seasonal data, we started from 24 months (1 year). The period of 256 (21 years), was chosen as maximum, since most variables did not show any significant power passed this value. | |
| Figure 2: A) Wavelet Spectra USATOUR, B) Wavelet Spectra VENTOUR, C) Wavelet Spectra HOLTOUR. | |
| The wavelet transform of USATOUR showed significant periodicity in the 3-6 years and 9-15 years, with peaks around 4 and 11.7 years. The highest peak was around 4 years. The wavelet transform of VENTOUR showed significant periodicity in the 2-4 years and 6-21 years, with peaks around 3, 8.4 and 18 years. The highest power was around 8.4 years. The wavelet transform of HOLTOUR showed significant periodicity near 4 years, between 6-9 years and 10-20 years. The highest peak was around 14 years, followed by the next peak of 7.2 years (Figure 2). | |
| The wavelet transformation of AUARAIN showed significant periodicity in the 3-7 years, with a high peak around 3.8 years and another peak at 5.7 years. The wavelet transformation of AUAWIND showed significant periodicity in the 3-8 years and 9-13 years. The peaks were at, respectively, 3.7, 5.6 and 10.7 years, where the peak around 5.6 was the highest. The wavelet transformation of AUATEMP showed no significant periodicity within the time-frame chosen. The wavelet transformation of USARAIN showed significant periodicity in the 3-4 years, 5-13 years and 14-19 years, peaks were around 3.3, 5.6 and the highest peak around 8.4 years. The wavelet transformation of USAWIND showed no significant periodicity within the timeframe chosen, whereas that of USATEMP showed no significant periodicity within the time-frame chosen. The wavelet transformation of VENRAIN showed significant periodicity in around 6 -7 years, 8-12 years and 17-19 years. The peaks for VENRAIN were 5.9 and 9.8 years. The wavelet transformation of VENWIND showed significant periodicity around 6-8 years, with a peak around 6.4 years. The wavelet transformation of VENTEMP showed significant periodicity in the 3-4 years, and 5-8 years. The peaks for VENTEMP were around 3.6 and 6.2 years. The wavelet transformation of HOLRAIN showed significant periodicity in around 4 years, between 5-9 years, and between 10-12 years, with a peak around 6.1 years. Both the wavelet transformation of HOLWIND and HOLTEMP showed no significant periodicity within the chosen time-frame. | |
| In order to detect and quantify correlations between variables that showed significant periodicity, wavelet coherences were calculated according to Gallegati and Semmler [51]. For the wavelet coherences only variables that showed significant periodicity between 24 to 256 months were used. Significant, periods that had relationships are given in years. The data are based from wavelet coherences across time, of two time-series [52,53]. | |
| Significant correlations where found for pull weather factors of rain and wind with tourism demand from the Northeast Sector of the United States and Holland. Both tourism demand sectors had relationships around 4 years. Rain pull factor also had a correlation with tourism demand from the Northeast Sector of the United States between 10-11 years. The wind-speed on Aruba had also a relationship with the tourism demand from the Northeast Sector of the United States around 5 years and a relationship with tourism demand from Holland near 2 years and tourism demand from Venezuela around 3 years. For push weather variables, it was noted that wind-speed near Caracas had a relationship with tourism demand from Venezuela, near 2 years and between 7-8 years. Air temperature near Caracas had also an influence with tourism demand from Venezuela between 6-7 years. Because some of these relationships in the cyclical patterns happened simultaneously at different locations, we decided to look into 2 main climate phenomena that can influence periodical weather patterns around the world. Climate does not influence populations through a single weather variable, but through a mix of weather features. Proxies for the overall climate condition can, at least at an early stage provide a robust estimation of the ecological influences of climate fluctuations, not least because the holistic account of the climate system [54]. We used the El Niño Southern Oscillation (ENSO) and the North Atlantic Oscillation (NAO), since these where shown to be of great use by other areas of study [54]. El Niño and La Niña, composes the El Niño Southern Oscillation (ENSO), which are periodic anomalies in sea surface temperatures (SSTs) in the equatorial Pacific Ocean. These warmer or cooler anomalies in ocean temperatures can influence weather patterns around the world by influencing high and low pressure systems, winds, and precipitation [55]. To measure ENSO, we used the Multivariate ENSO index (MEI) [56]. The North Atlantic Oscillation consists of a north-south dipole of anomalies, with one center placed over Greenland and the other center of opposite sign spanning the central latitudes of the North Atlantic between 35 and 40 degrees north. The positive phase of the NAO mirrors belownormal heights and pressure across the high latitudes of the North Atlantic and above-normal heights and pressure over the central North Atlantic, the eastern United States and Western Europe. The negative phase of NAO reflects the opposite. Both phases of the NAO are associated with changes in temperature and precipitation patterns often extending from eastern North America to western and central Europe [57]. | |
| The wavelet transformation of MEI, showed peaks in periodicity around 2.6, 3.7, 5 and 11 years. The highest peak in periodicity for MEI was around 3.7 years. The wavelet transformation of NAO, showed peaks in periodicity around 2.5, and 11.6 years. The highest peak in periodicity for NAO was around 2.5 years. Following Johansson, Cummings and Glass [31], the authors proceeded to calculate wavelet coherences between the relevent variables, and phase differences in order to find the relationship between the variables. The variable MEI showed significant coherence with USATOUR in the periods of 2-3 year, 4 years and 10-15 years (Figure 3a). MEI showed also a significant coherence with the variable HOLTOUR in the period of 2-3 years (Figure 3b). For the North Atlantic Oscillation (NAO) we noticed a significant relationship around 2 years, and 10-14 years with respect to USATOUR (Figure 4a). For HOLTOUR we did not find a relationship and for the VENTOUR a significant coherence was found around 8 years (Figure 4b). | |
| Figure 3: A) Average Wavelet Coherence Power USATOUR, MEI, B) Average Wavelet Coherence Power HOLTOUR, MEI. | |
| Figure 4: A) Average Wavelet Coherence Power USATOUR, NAO, B) Average Wavelet Coherence Power VENTOUR, NAO. | |
| Similar to Johansson et al. [31] we can deduct from the phase difference calculations for the period between 2-3 years and between the years 1986 and 1987 that increased ENSO leads tourism demand from the North East United States by 6 months (Figure 5a). The years 1986-1987 were also a moderate ENSO year according the Climate Prediction Center [58]. The causality hints that El Niño events that oscillate between 2-3 years would act as a pull factor for tourist from the North East sector of the United States. The period of 4 years showed small areas of wavelet coherence, and therefore they are unlikely to be causal taken on their own [59]. According Keener et al. [59] more extensive areas of significance, are less likely to be due to chance and should be included in the analysis for additional relationships to a physical mechanism. For the period of 10-15 years, it looked like causality by chance. This is due to the fact that the phase difference analysis varied in the period, from MEI (ENSO) leading tourism demand from to North Eastern United States, to tourism demand leading MEI (ENSO). Since this would be contradictory, we dropped the coherence in the period of 10 to 15 years as coherence by chance. The fluctuation of the signal in the same time-period would also be useless for forecasting purposes (Figure 5). | |
| Figure 5: A) Phase Angle USATOUR, MEI (ENSO) (1986-1987), B) Phase Angle HOLTOUR, MEI (ENSO) (2007-2009). | |
| The phase difference for the period between 2-3 years and between 2007 and 2009 showed that a decrease in ENSO leads an increase in tourism demand from the Netherlands (Figure 5b). This hints that a La Niña episode would cause eventually an increase in Dutch tourists. | |
| ENSO will usually have an influence on weather patterns, and therefore, we would expect that some of the weather pull or push factors could have, also, an influence. Calculations showed that AUARAIN would have an influence on USATOUR and HOLTOUR. Past literature showed that rain increases during La Nina events while rain decrease during El Nino events on Aruba [60]. This would indicate that USATOUR would increase during less rain events on Aruba, while HOLTOUR would increase during more rain events on Aruba. Previous research has shown that strong El Nino’s could increase rain in the Netherlands during spring and that La Nina had no influence on the rain pattern on Holland [61]. This would indicate that a La Nina event would not act as a push factor on tourism demand from Holland, but more like a pull factor from Aruba. Although at first sight it would not be logical that more rainfall would attract a tourist to a destination, the authors believe that maybe a more detailed study needs to be conducted on the travel perception of the Dutch tourist. Maybe the Dutch tourist would prefer a destination with more vegetation, compared to a drought stricken destination. Another caveat could be that other destinations that the Dutch tourist would have chosen over Aruba, where more heavily influenced by un-attractive climate conditions due to La Nina compared to Aruba. Finally, the relationship could indicate that the heavy tourism marketing of Aruba could have influence the Dutch tourist to choose Aruba, even during anomalous rainfall periods. | |
| With respect to NAO, we noticed a significant relationship around 2 years, and 10-14 years for USATOUR and around 8 years for the VENTOUR. The phase difference for USATOUR for the period around 2 years between 1981-1982 and 1990-1991 showed that an increase in USATOUR would be related to a decrease in NAO, where USATOUR leads NAO (Figure 6a). The phase periods for other years, within the two-year period, where dropped due to their short periods of length. The phase difference for USATOUR for the period between 10-14 years indicated that for the period from 1992-2015, NAO and USATOUR would be in phase were NAO would lead USATOUR (Figure 6b). The relationship between NAO and USATOUR for the short period of 2 years indicates that temperature could be a culprit, since during negative phases of NAO, the eastern part of the USA is colder, and drier [54] (Figure 6). Since the authors did not find any relationship between long-term temperature deviations and longterm deviations from tourism demand from the Northeast sector and the relationship between drier weather conditions and more tourism demand from the northeast sector of the USA is not logical, they dropped the relationship between the NAO and USATOUR for the period of 2 years. The relationship between USATOUR and NAO for the 10-14 years indicated that positive phases of NAO would lead to an increase of tourism demand from the Northeast sector. Positive phases of NAO usually relate to wetter and warmer conditions on the eastern USA [54]. In the current study, the authors did not find any relationships with USARAIN, and USATOUR. Therefore, precipitation cannot be considered as a push factor. Since the authors did not find any relationships with temperature they did not consider temperature as a significant push factor, too. It is also not logical that warmer temperature at a location would induce a tourist to go to an even warmer destination. Wind could, also, not act also as a push factor since no coherence was found between USAWIND and USATOUR. During positive NAO conditions one would expect drier and breezer conditions on Aruba, due to a stronger than average atlantic surface pressure and stronger upwelling near Aruba [62,63]. These conditions would corroborate on earlier findings on the Aruban wind and rain relationship and tourism from the United States. This would suggest that wind and rain conditions on Aruba would act as a pull factor, and explain the relationship between positive NAO anomalies and toursim from the United States. | |
| Figure 6: A) Phase Angle USATOUR, NAO (1981-1982), B) Phase Angle USATOUR, NAO (1992-2015). | |
| The phase difference for VENTOUR and NAO for the period around 8 years indicated that for the period from 1991-1985 and 2012- 2015, VENTOUR and NAO would be in phase were NAO would lead VENTOUR. This pattern indicates that positive values of NAO would cause Venezuelans to travel to Aruba. Since any effect of a positive phase of NAO would be the same for Aruba as for Venezuela, the authors dropped this relationship. Past literature shows that positive NAO conditions would relate to drier Caribbean, including northern part of Venezuela, due to subsidence and sea surface temperature anomalies [62]. These manifest themselves due to a stronger than average Atlantic high pressure area. | |
Conclusion |
|
| This study hints that tourism is evidently connected to long-term climate signals. Past literature showed that tourism literature has paid not much attention to the effects of meteorological factors to explain tourism flow and a great majority of the international tourismdemand models do not contain climate and weather conditions as explanatory variables [26]. The main objective of this study was to underline that long-term climate factors matter in tourism, and that they should be taken into account. The authors specifically investigated the existence of statistical relationship between 3 main push and pull climate variables (rain, temperature and wind) and tourism demand from many markets, namely USA, the Netherlands and Venezuela. They further looked into the climate factors, by incorporating two important modes of atmospheric variability, the NAO and ENSO, and investigated their possible relationships with tourism demand from the three markets. Results indicated that rain would act as a pull factor for the North-Eastern USA, and the Netherlands; wind would act as a pull factor for the North-Eastern USA, the Netherlands and Venezuela. We further noticed that ENSO events had an influence on the tourism demand from the United States and the Netherlands. The NAO also had an influence on the tourism demand from the United States. The present study adds some important contributions to the existing literature pertaining to tourism and climate on small island states, especially related to the two atmospheric variables: | |
| A. Although some previous studies had already examined the influence of NAO and tourism, and ENSO influences on energy, agriculture and transport activities, it is to our knowledge, the first time that the effects of ENSO and NAO themselves on tourism have been looked for small island states, whereby several tourism markets were combined. The study by Álvarez-Díaz, Giráldez, & González-Gómez [26], focused more on a develop country (Spain). | |
| B. The results of this study indicate that two important atmospheric variability, the NAO and ENSO, have an influence on tourism demand from the USA, the Netherlands. The influences manifests themselves in possible push and pull climate factors. | |
| C. The results imply that a NAO or ENSO index can be useful to tourism in general. When constructing a possible tourism demand model the NAO or an ENSO index as the MEI can be used as explanatory variables to tourism demand. According to Alvarez-Diaz et al. [26] one can get parsimonious models since one can introduce into a model meteorological informations using less variables. | |
| D. According to Alvarez-Diaz et al. [26], meteorological data summarized in, for example, a NAO index can be useful in the operational decission-making process and risk management of business in the tourism sector. The same idea can be implemented when considering an ENSO index such as MEI. | |
| The results also have managerial implications. Policy makers and other key decision makers need to understand the combined influence of cyclical oscillations of push and pull climate elements on oscillations of tourism demand. According to Hamilton and Lau [64] climate is conceivably the third-most important trait in tourists’ decision making process, after the aquatic and natural attributes of a destination. This study shows that monitoring economic factors alone is not enough when it comes to analyzing the determinants of tourism demand for Aruba. Climate patterns have an influence on travelers from the Netherlands, the USA and Venezuela to Aruba. Knowledge about the structure of the climate variations could assist tourism managers and government representatives to (better) cope with long-term demand fluctuations in their planning, forecasting, and marketing efforts. For example, one possible strategy that policy makers and tourism leaders could follow would be to keep an eye on longerterm climate forecasts, for ENSO conditions such as that of the International Research Institute for Climate and Society (http://iri.columbia.edu/our-expertise/climate/forecasts/enso/current/) in order to get a lead on expected cyclical climate conditions such as ENSO and oscillation in tourism demand from the North-Eastern USA and the Netherlands. For instance, if an El Niño event is foreseen than the likelihood of higher tourism demand from the North-Eastern USA increases,while the tourism demand from the Netherlands decreases. Policy makers and tourism chiefs in Aruba could react to this information increasing marketing efforts for the Netherlands, while decreasing marketing efforts for the North- Eastern USA thereby compensating for the expected fall-down in demand from the Netherlands. | |
| Finally, in spite of the promising results, the present study was limited to only 30 years of tourism demand for only the island of Aruba. It is recommended to add other destinations in the Caribbean and find destinations that have longer tourism demand data to give further insight into the relationships found. Also as indicated by Álvarez-Díaz, Giráldez, & González-Gómez [26] studies such as this one represent only a first step that opens a new line of research possibilities. Futher research will be needed in order to construct a tourism-demand model that includes the NAO index as an explanatory variable to further quantify and explain the impacts of NAO on tourism. Our study hints that an ENSO index should also be included in such a tourism-demand model. | |
References |
|
|
|
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi